Question

At one end A of a diameter AB of a circle of radius 5 cm, tangent $XAY$ is drawn to the circle. Find the length of the chord $CD$ parallel to XY and at a distance 8 cm from A .

Options

A. 4 cm
B. 5 cm
C. 6 cm
D. 8 cm

Answer

D

Explanation

First, drow a circle of radius 5 cm having center O.A tangent XY is drawn at point A.

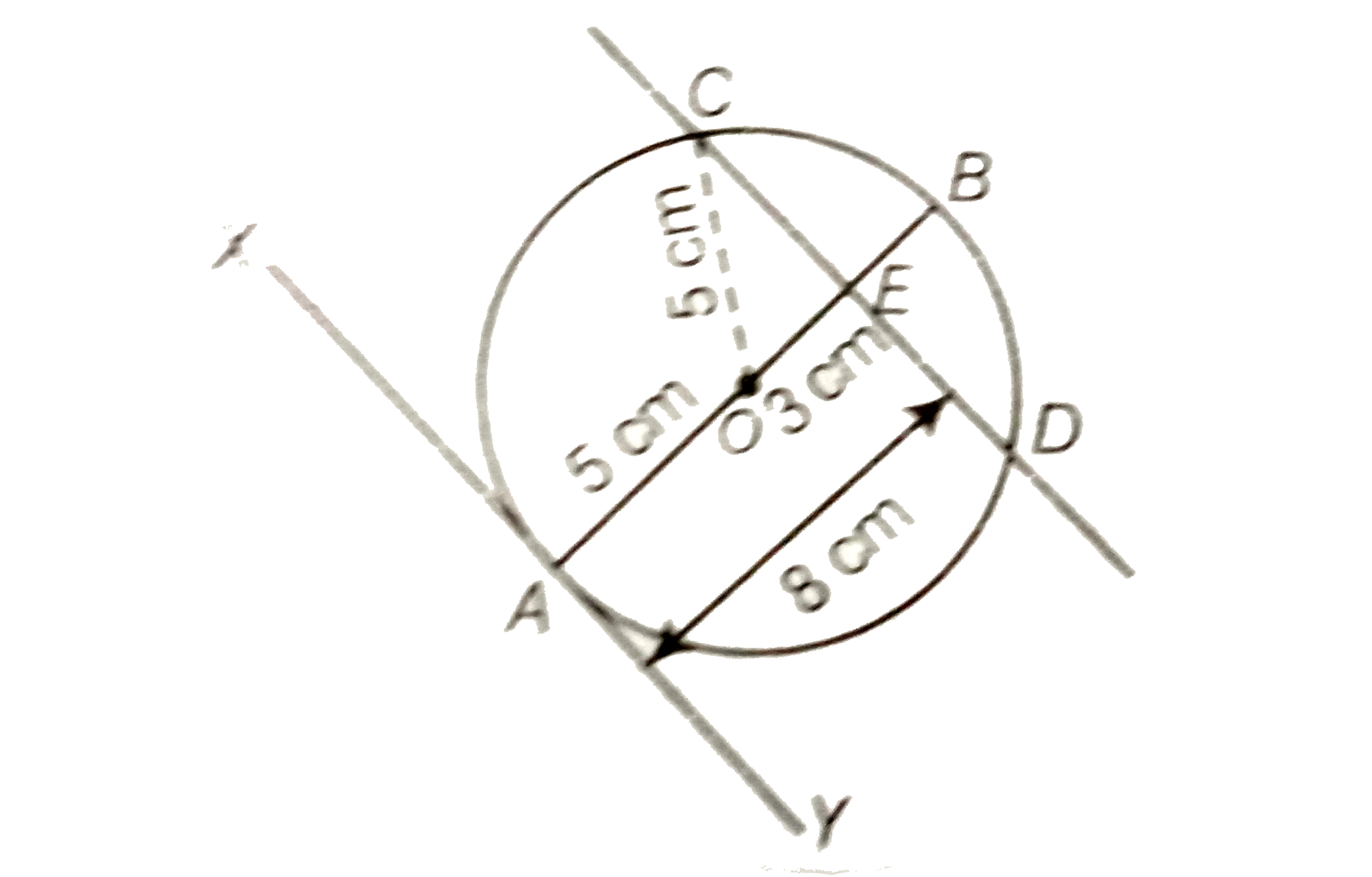
A chord CD is drawn which is parallel to XY and at a distance of 8 cm from A.
Now, `angleOAY=90^(@)`
[Tangent and any point of a circle is perpendicularl to the radius through the point of contact]
`DeltaOAY+DeltaOED=180^(@)` [:' sum of cointerior is `180^(@)`]
`rArrDeltaOED=180^(@)`
Also, `AE=8cm.` Join OC
Now, in right angled `DeltaOEC,` `OC^(2)=OE^(2)+EC^(2)`
`rArrEC^(2)=OC^(2)-OE^(2)` [by Pythagoras theorem]
`=5^(2)-3^(2)`
`[:' OC=radius=5cm, OE=AE=-AO=8-5=3cm]`
`=25-9=16`
`rArrEC=4cm`
Hence, length of chord `CD=2C E=2xx4=8cm`
[since, perpendicular from centre to the chord bisects the chord]