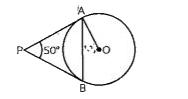
In figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
A
25∘
B
30∘
C
40∘
D
50∘
Video Solution
Text Solution
The correct Answer is:A
Given, PA and PB are tangent lines.
:. PA=PB
[since, the length of tangents drawn from an external point to a circle is equal]
⇒∠PBA=∠PAB=0 [say]
In ΔPAB, ∠P+∠A+∠B=180∘
[since, sum of angles of a triangle =180∘]
⇒50∘+0+0=180∘
⇒20=180∘−50∘=130∘
⇒0=65∘
Also, OA⊥PA
[since, tangent at any point of a circle is perpendicular to the radius through the point of contact]
∴∠PAO=90∘
⇒∠PAB+∠BAO=90∘
⇒65∘+∠BAO=90∘
⇒∠BAO=90∘−65∘=25∘
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If PA and PB are tangents to the circle with centre O such that ∠APB=50∘ then ∠OAB is equal to
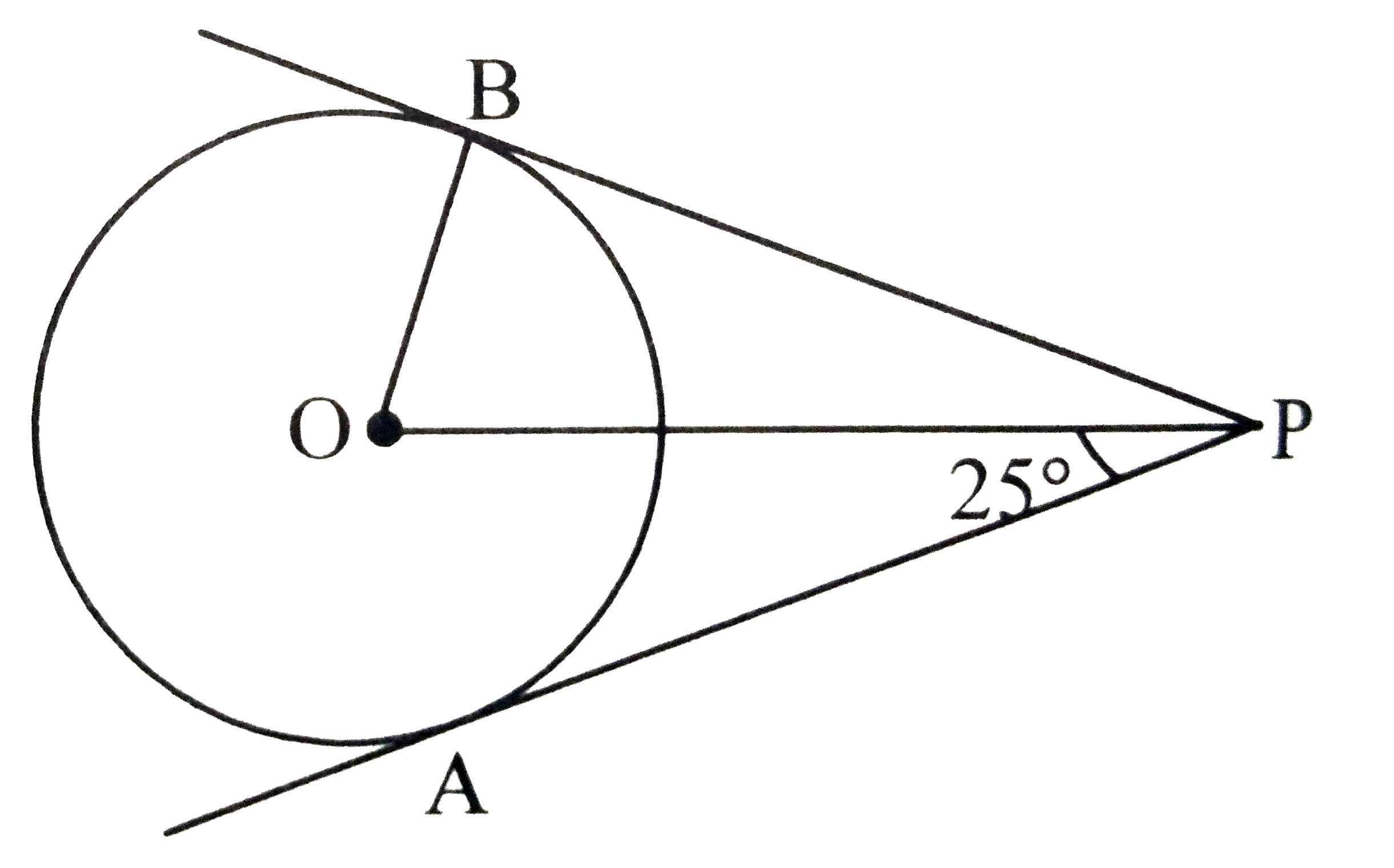
A50∘B30∘C40∘D25∘In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
A36∘B18∘C27∘D36∘If PA and PB are two tangents to a circle with centre O such that ∠APB=80∘, then, ∠AOP=?
A40∘B50∘C60∘D70∘
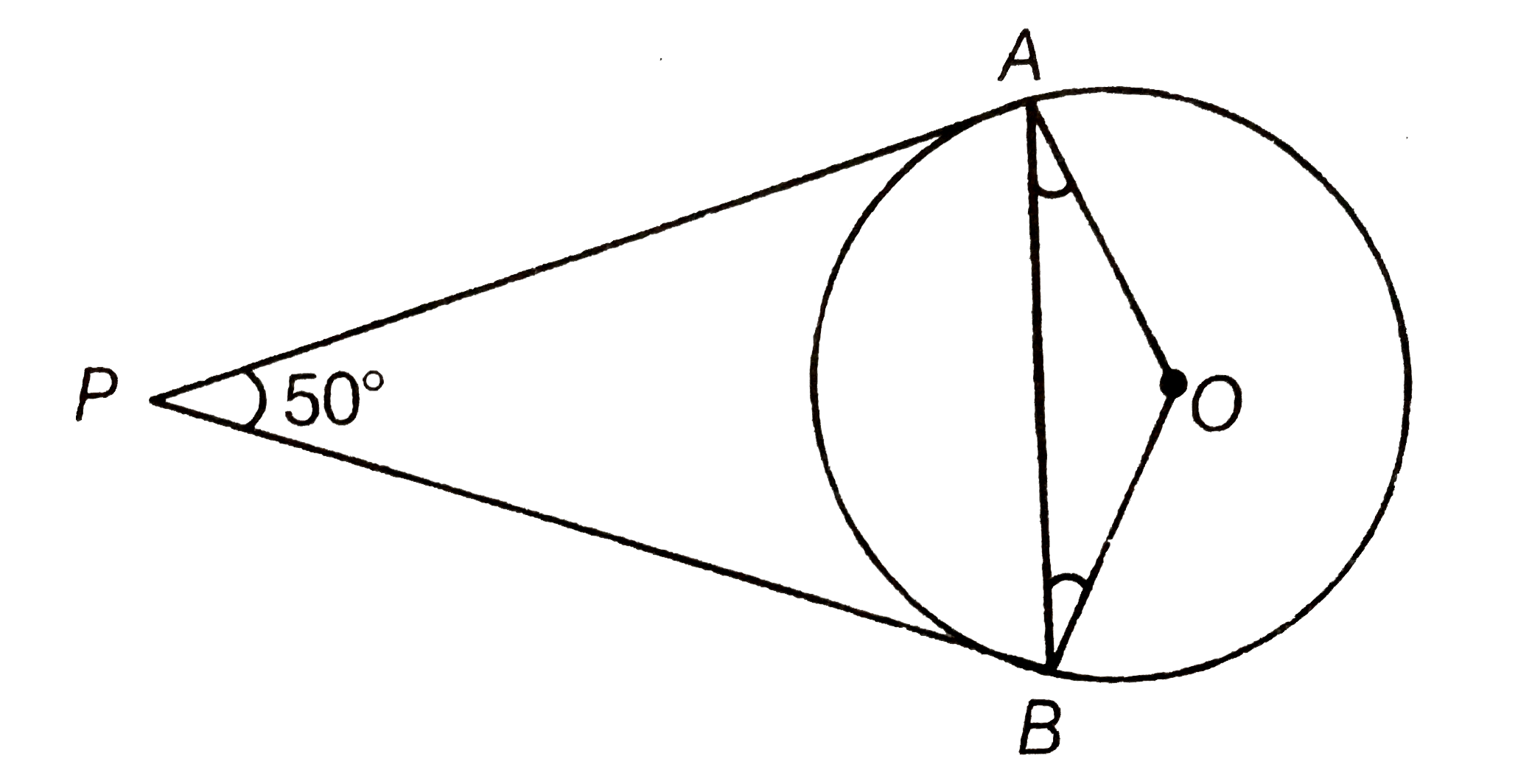
In the given figure, PA and PB are tangents to a circle with centre O. Prove that ∠APB and ∠AOB are supplementary.

View SolutionIn Fig. 10.77, PA and PB are tangents to the circle with centre O such that ∠APB=50o . Write the measure of ∠OAB . (FIGURE)
View SolutionAssertion (A) : PA and PB are triangles to a circle with centre O such that ∠AOB=110∘, then ∠APB=90∘
Reason (R ) : The length of two tangents drawn from an external point are equal .
View SolutionPA and PB are the tangent on a circle with centre O such that ∠APB=42∘. What will be the value of ∠AOB?
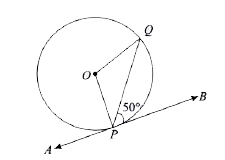
View SolutionIn figure , APB is a tangent to a circle with centre O at point, If ∠QPB=50∘ , then the measure of ∠POQ is
View Solution