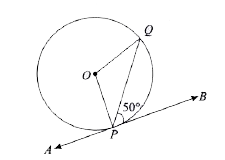
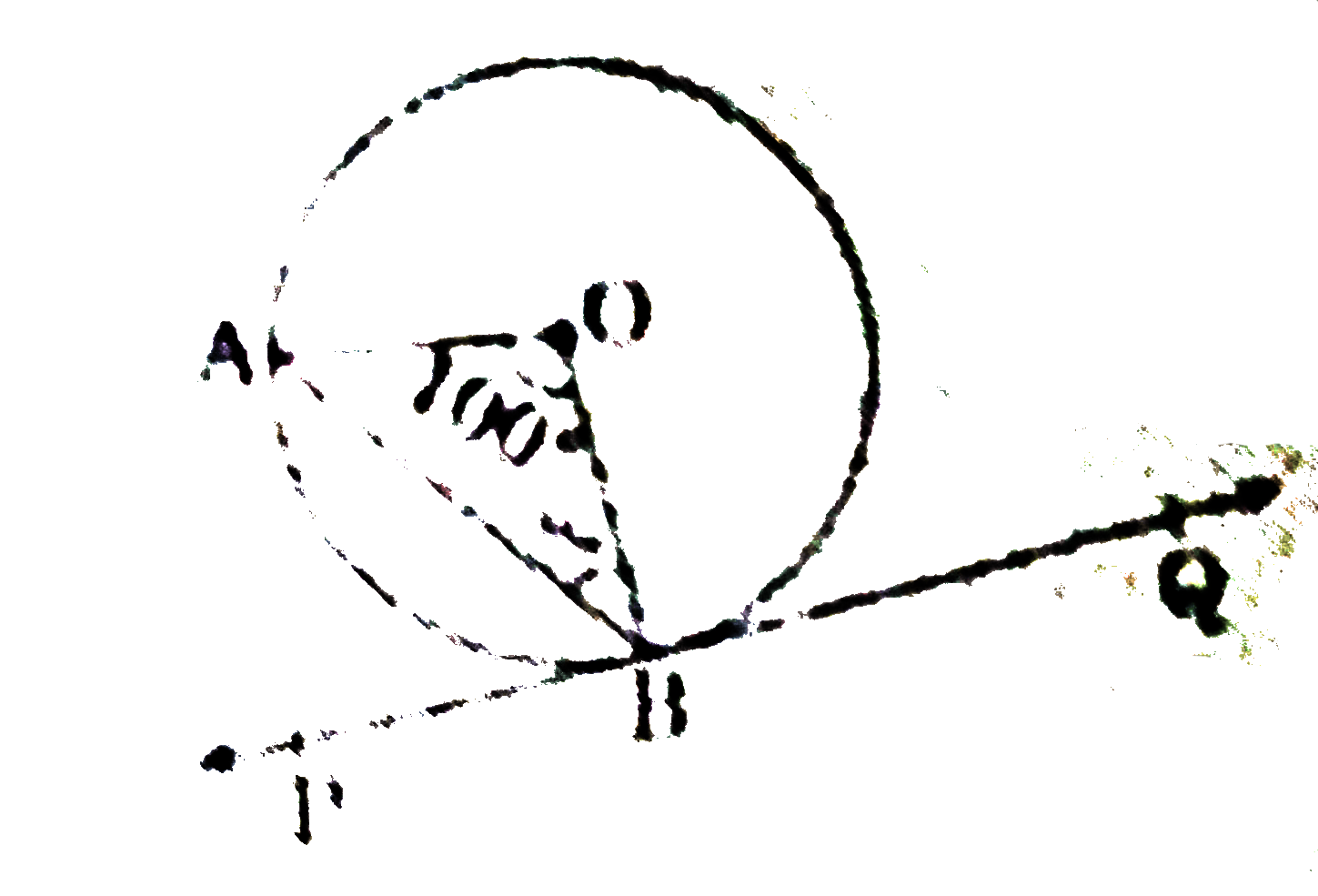In figure , APB is a tangent to a circle with centre O at point, If ∠QPB=50∘ , then the measure of ∠POQ is
100∘
120∘
140∘
150∘
The correct Answer is:A
Topper's Solved these Questions
- TANGENTS TO CIRCLES Book:CENGAGEChapter:TANGENTS TO CIRCLES Exercise:OLYMPIAD AND NTSE LEVEL EXERCISES
Explore 10 Videos
- TANGENTS TO CIRCLES Book:CENGAGEChapter:TANGENTS TO CIRCLES Exercise:TEST YOURSELF (LEVEL 2)
Explore 4 Videos
- STANDARD AND ALLIED ANGLESBook:CENGAGEChapter:STANDARD AND ALLIED ANGLESExercise:Olympiad And NTSE Level Exercises
Explore 10 Videos
- TRANSFORMATIONSBook:CENGAGEChapter:TRANSFORMATIONSExercise:Olympiad and NTSE level exercises
Explore 10 Videos
Similar Questions
Knowledge Check
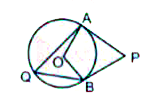
In the given figure, AP and BP are tangents to a circle with centre O. IF ∠APB=62∘ then the measure of ∠AQB is
 Aa) 59∘Bb) 28∘Cc) 118∘Dd) 31∘
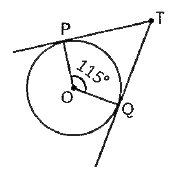
Aa) 59∘Bb) 28∘Cc) 118∘Dd) 31∘In the figure, TP and TQ are tangents drawn to the circle with centre at O. If ∠POQ=115∘ then ∠PTQ is:
 A115∘B57.5∘C55∘D65∘
A115∘B57.5∘C55∘D65∘
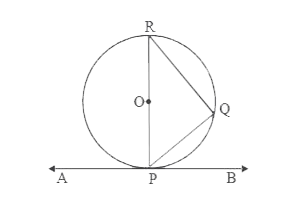
In the given figure, AB is a tangent to a circle with centre O. Prove ∠BPQ=∠PRQ.
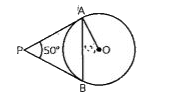
View SolutionIn the figure, PA and PB are tangents to the circle with centre O such that ∠APB=50∘, and the measure of ∠OAB is …………
View SolutionIn the figure, PA is a tangent from an external point P to the circle with centre O and diameter AB. If ∠POB=110∘, then the measure of ∠APO is:
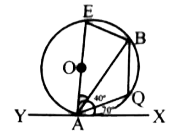
View SolutionIn the figure XY is a tangent to the circle with centre O at A. If ∠BAX=70∘,∠BAQ=40∘ then ∠ABQ is equal to :
View SolutionIn Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘
View SolutionIn Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘
View Solution