From a point P which is at a distance of 13 cm from the center O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle is drawn. Then, the area of the quadrilateral POQR is

A

$60 c m^{2}$

B

$65 c m^{2}$

C

$30 c m^{2}$

D

$32.5 c m^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Fistly, draw a circle of radius 5 cm having center O.P is a point at a distance of 13 cm from O.A pair of tangents PQ and PR are drawn.

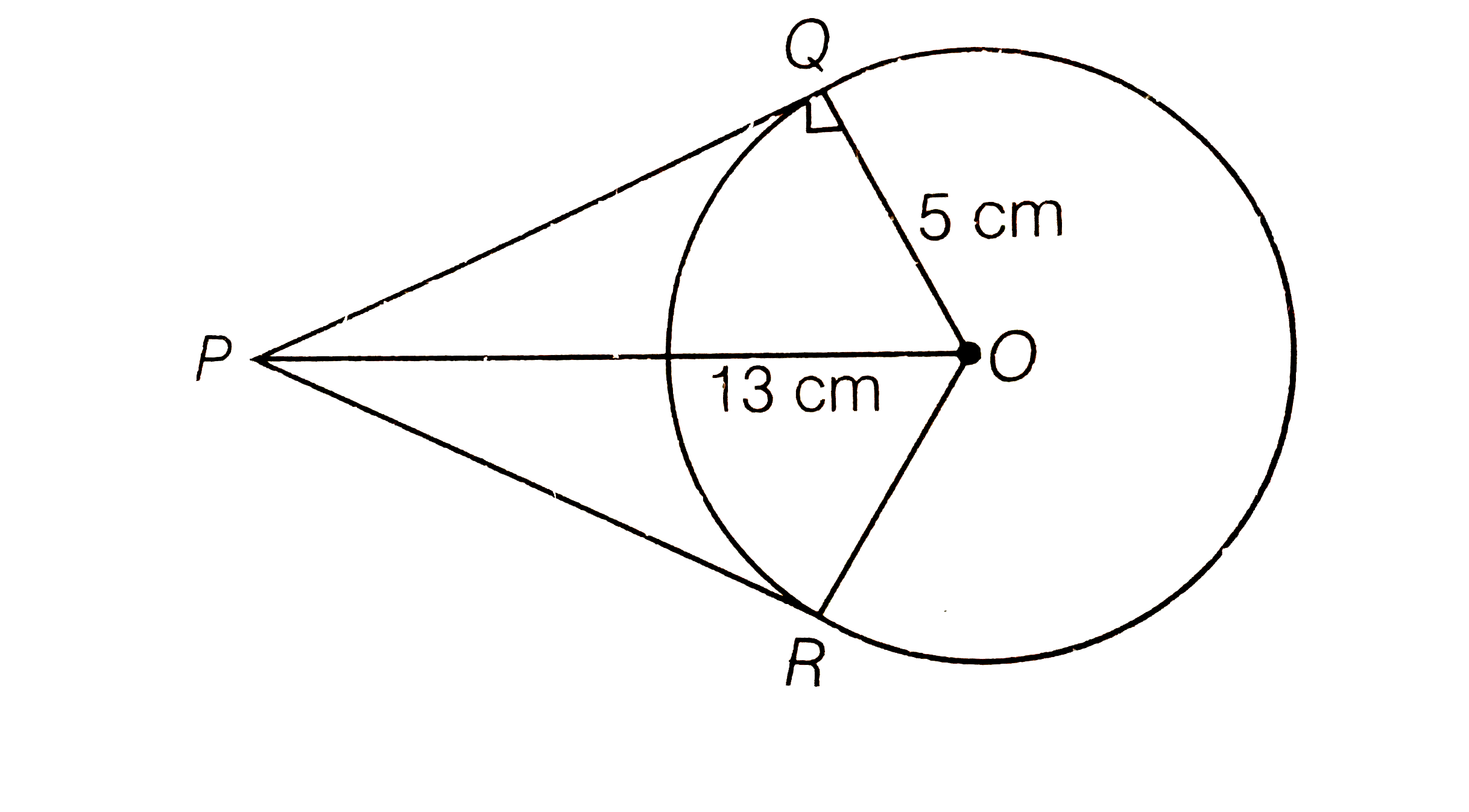
Thus, quadrilateral PQOR is formed.
$∵ O Q ⊥ Q P$ [since, AP is a tangent line]
In right angled $Δ P Q O,$ $O P^{2} = O Q^{2} + Q P^{2}$
$\Rightarrow 13^{2} = 5^{2} + Q P^{2}$
$\Rightarrow Q P^{2} = 169 - 25 = 144$
$\Rightarrow Q P = 12 c m$
Now, area of $Δ O Q P = \frac{1}{2} \times Q P \times Q O$
$= \frac{1}{2} \times 12 \times 5 = 30 c m^{2}$
:. Area of quadrilateral $Q O R P = 2 Δ O Q P$
$= 2 \times 30 = 60 c m^{2}$

|

Updated on:21/07/2023

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is :
A60 $c m^{2}$
B65 $c m^{2}$
C30 $c m^{2}$
D32.5 $c m^{2}$
Question 2 - Select One
From a point P which is at a distance of 13 cm from centre O of a circle of radius 5 cm, in the same plane, a pair of tangents PQ and PR are drawn.area of quadrilateral PQOR is
A $65 c m^{2}$
B $60 c m^{2}$
C $30 c m^{2}$
D $90 c m^{2}$
Question 3 - Select One
From a point P which is at a distance of 10 cm from the centre O of a circle of radius 6 cm, a pair of tangents PQ and PR to the circle at point Q and P respectively, are drawn. Then the area of the quadrilateral PQOR is equal to
A30 sq.cm
B40 sq.cm
C24 sq.cm
D48 sq.cm

NCERT EXEMPLAR-CIRCLES-Circles

Home
Ask Doubt
Profile