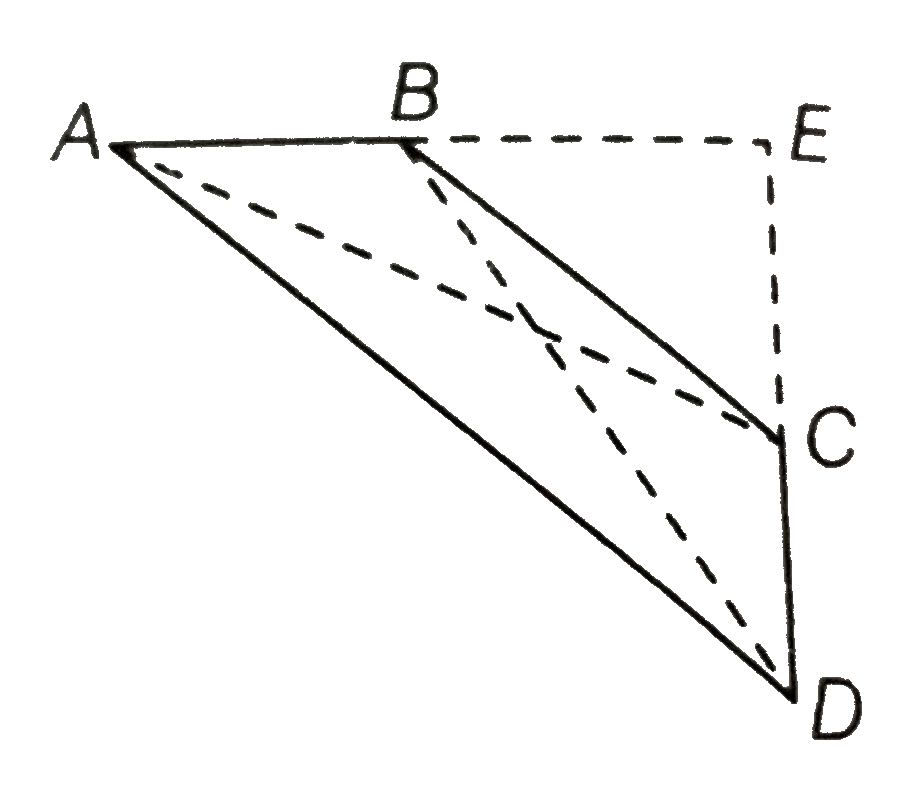
In a quadrilateral ABCD, $∠ A + ∠ D = 90^{\circ}$ . Prove that
$A C^{2} + B D^{2} = A D^{2} + B C^{2}$

Video Solution

Text Solution

Verified by Experts

Given Quadrilateral ABCD, in which $∠ A + ∠ D = 90^{\circ}$
To prove $A C^{2} + B D^{2} = A D^{2} + B C^{2}$
Construct Produce AB and CD to meet at E.
Also, join AC and BD.
Proof In $Δ A E D, ∠ A + ∠ D = 90^{\circ}$ [given]
$∴ ∠ E = 180^{\circ} - (∠ A + ∠ D) = 90^{\circ}$
[ $∵$ sum of angles of a triangle= $180^{\circ}$ ]
Then by Pythagoras theroem, $A D^{2} = A E^{2} + D E^{2}$
In $Δ B E C$ , by pythagoras theorem, $B C^{2} = B E^{2} + E F^{2}$
On adding both equations, we get
$A D^{2} + B C^{2} = A E^{2} + D E^{2} + B E^{2} + C E^{2}$ ..(i)
In $Δ A E C$ , by Pythagoras therom,
$A C^{2} = A E^{2} + C E^{2}$
and in $Δ B E D$ , by pythagoras theorem
$B D^{2} = B E^{2} + D E^{2}$
On adding both equation weget
$A C^{2} + B D^{2} = A E^{2} + C E^{2} + B E^{2} + D E^{2}$ ...(ii)
From Eqs. (i) and (ii),
$A C^{2} + B D^{2} = A D^{2} + B C^{2}$ Hence proved

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

BOOK - NCERT EXEMPLARCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Surface Areas And Volumes
62videos
SURFACE AREAS AND VOLUMES

Similar Questions

NCERT EXEMPLAR-TRIANGLES-Triangles

Home
Ask Doubt
Profile