In given figure PQR is a right angled triangle, right angled at Q and QS⊥PR. If PQ=6 cm and PS=4cm, then find QS, RS and QR.

Video Solution
Text Solution
Given ΔPQR in which ∠Q=90∘,QS⊥PR and PQ=6 cm, PS=4cm
In ΔSQPandΔSRQ,
∠PSQ=∠RSQ [each equal to 90∘]
∠SPQ=∠SQR [each equal to 90∘−∠R]
∴ΔSQP~ΔSRQ
Then, SQPS=SRSQ
⇒SQ2=PS×SR ...(i)
In right angled ΔPSQ,PQ2=PS2+QS2 [by Pythagoras theorem]
⇒(6)2=(4)2=QS2
⇒36=16+QS2
⇒QS2=36−16=20
∴QS=√20=2√5cm
On puttting the value of QS in Eq. (i) we get
(2√5)2=4×SR
⇒SR=4×54=5cm
In right angled ΔQSR,QR2=QS2+SR2
⇒QR2=(2√5)2+(5)2
⇒QR2+20+25
∴QR=√45=3√5cm
Hence, QS=2√5 cm RS= 5 cm and QR= 3√5 cm
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, triangle PQR is a right angled triangle at Q. If PQ = 35 cm and QS = 28 cm, then what is the value (in cm) of SR?
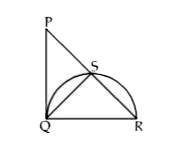 A35.33B41.33C37.33D43.33
A35.33B41.33C37.33D43.33In the figure below, PQR is a right-angled triangle, right angled at P. A perpendicular line PS is drawn from P to QR. PR = 5 cm and PQ = 12 cm.
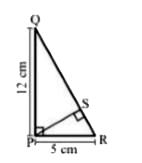
What is RS:SQ?A5:12B13:17C13:60D25:144In a triangle PQR, PQ=20 cm and PR =6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of the above
In the given figure, triangle PQR is a right angled triangle at Q. If PQ = 35 cm and QS = 28 cm, then what is the value (in cm) of SR?

View SolutionIn ΔPQR right angled at Q , PQ = 3 cm and PR = 6 cm .
Determine side QR.
View SolutionIn the following figure, △PQR is right-angled at R and S is the mid-point of hypotenuse PQ. If RS=25cm and PR=48cm, then find QR.
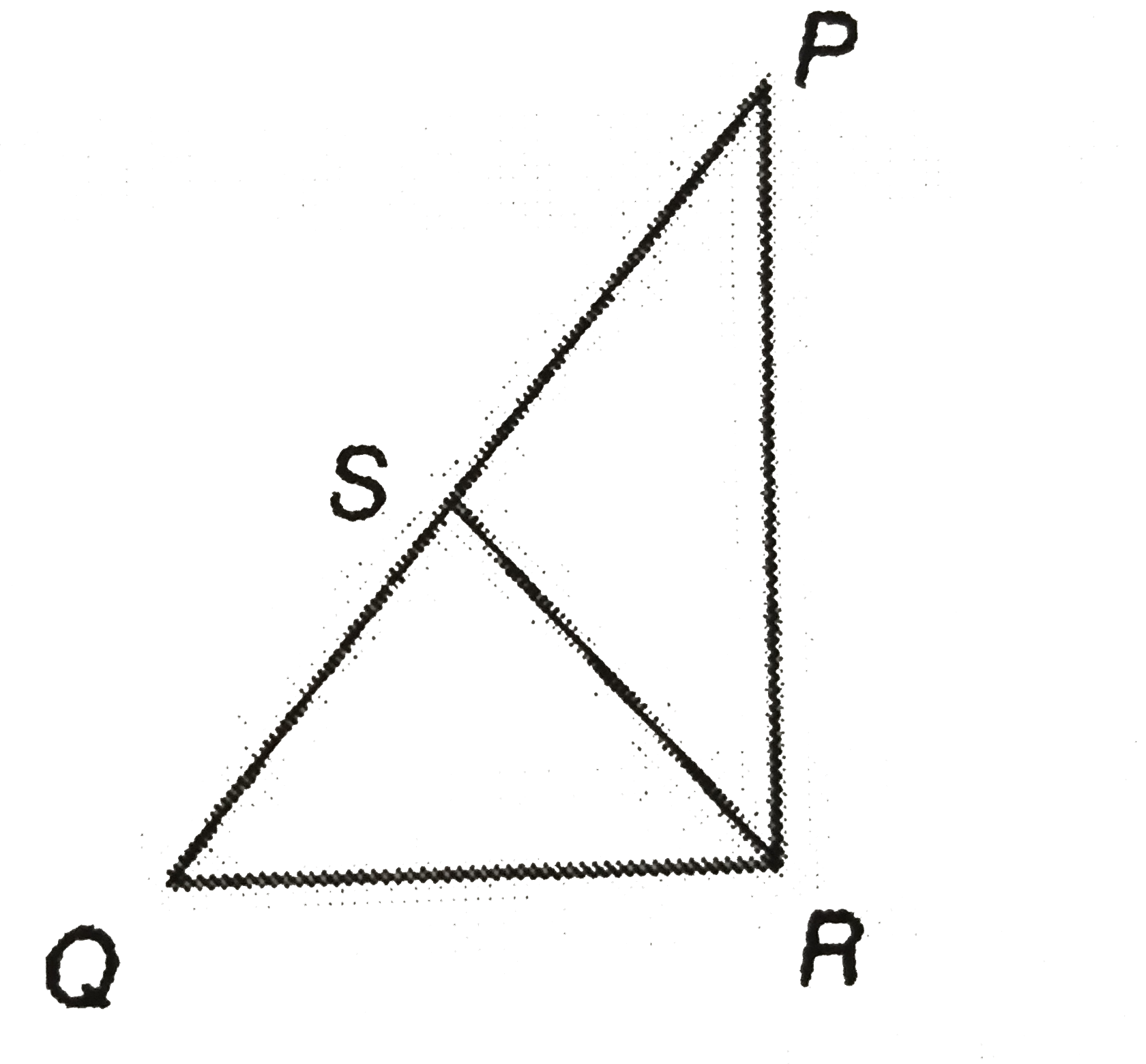
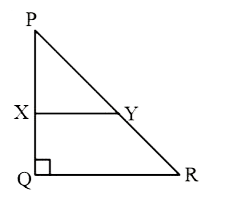
View SolutionIn the given Fig. PQR is a triangle, right angled at Q. If XY || QR, PQ =6 cm, PY= 4 cm and PX : XQ= 1 : 2. Calculate the lengths of PR and QR.
View SolutionIn right-angled triangle PQR, if ∠P=60∘,∠R=30∘andPR =12, then find the values of PQ and QR.
View Solution
