In given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
Video Solution
Text Solution
GivenΔABC in which∠B=90∘andBD⊥AC
Also, AD=4 cm and CD= 5 cm
In ΔADBandΔCDB,∠ADB=∠CDB [each equal to 90∘]
and ∠BAD=∠DBC[each equal to 90∘−∠C]
∴ΔDBA~ΔDCB [by AAA similarity criterion]
Then, DBDA=DCDB
⇒DB2=DA×DC
⇒DB2=4×5
⇒DB=2√5cm
In right angled ΔBDC,BC2=BD2+CD2 [by phythogoras therom]
⇒BC2=(2√5)2+(5)2
=20+25=45
⇒BC=√45=3√5
Again, ΔDBA~ΔDCB
∴DBDC=BABC
⇒2√55=BA3√5
∴BA=2√5×3√55=6cm
Hence, BD=2√5 cm and AB= 6 cm
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a class of 39 students the ratio of boys and girls is 2 : 1. Radhika ranks 15th among all the students from top and 8th among girls from bottom. How many boys are there below Radhika ?
AA) 9BB) 17CC) 11DD) 15
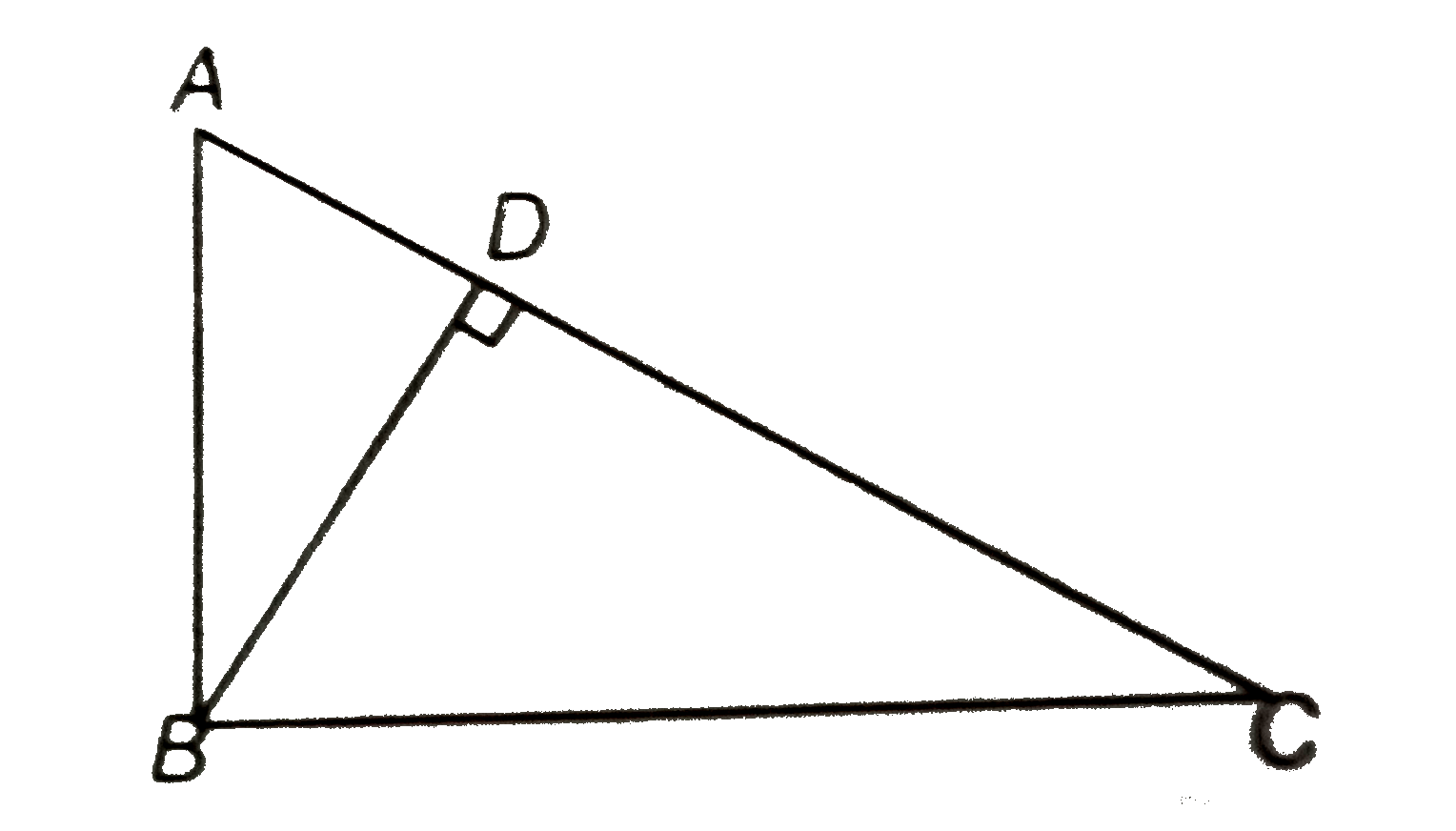
In the figure , ABD is a triangle right angled at A and AC ⊥ Bd . Show that

AD2=BD⋅CD
View SolutionIn the given figure,ABC in a right-angled triangle,right-angled atB.IfBC=5cmandAC-AB=1cm,f∈dthevalueofcosecAandcos A
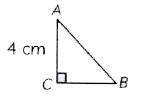
View SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
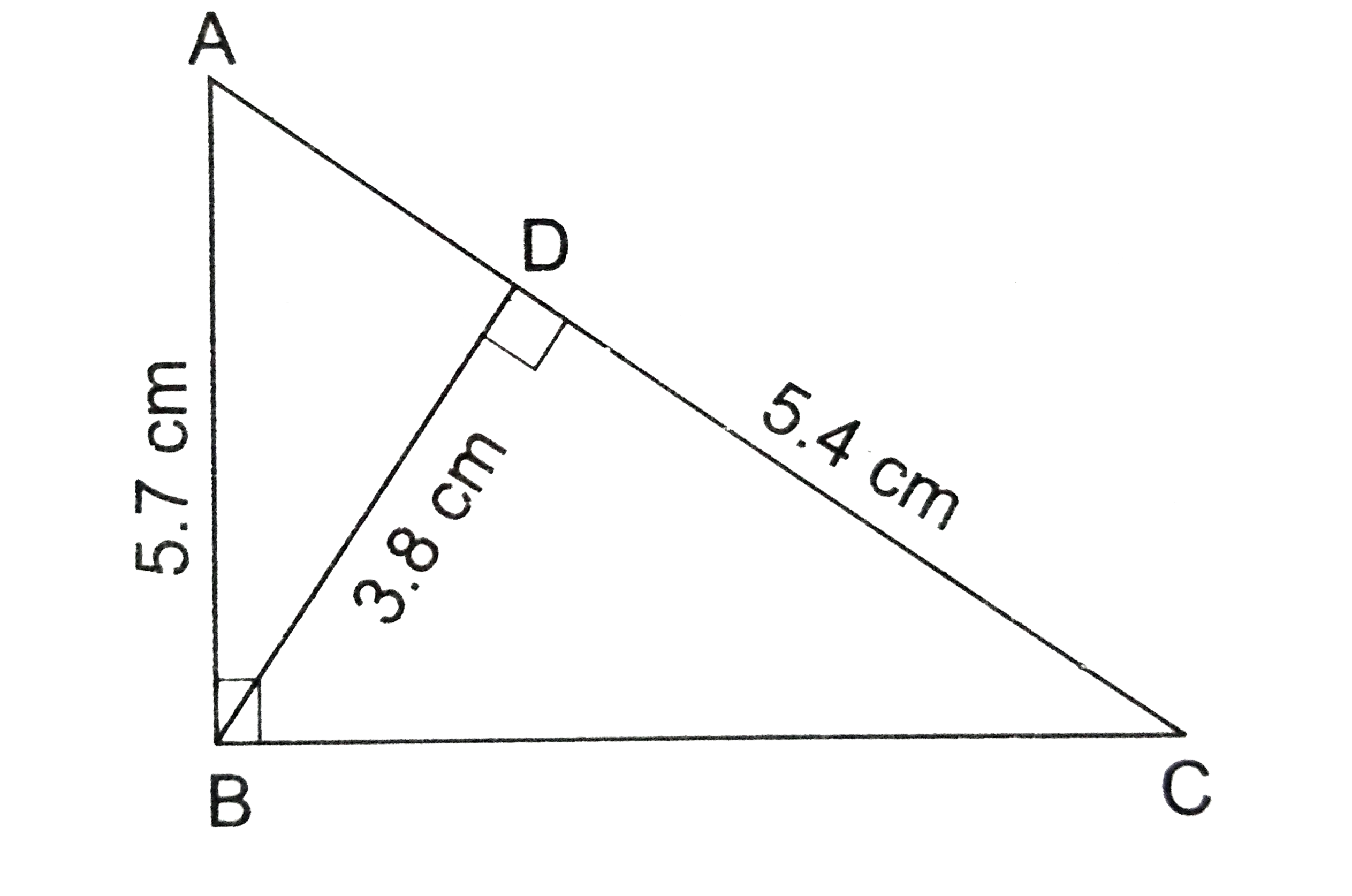
View SolutionIn the given figure, ∠ABC=90∘andBD⊥AC. If AB=5.7cm,BD=3.8cmandCD=5.4cm, find BC.
View SolutionIn the given figure, AD is the bisector of ∠BAC. If AB =10 cm , AC=6 cm and BC=12 cm, find BD and DC .
View SolutionABC is a triangle right angled at A and AD is perpendicular to BC. If BD = 8 cm and DC =12.5 cm, then what is AD equal to ?
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that
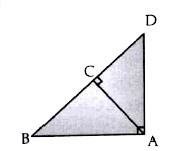
AD2=BD×DC
View Solution
