Equilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.

Video Solution

Text Solution

Verified by Experts

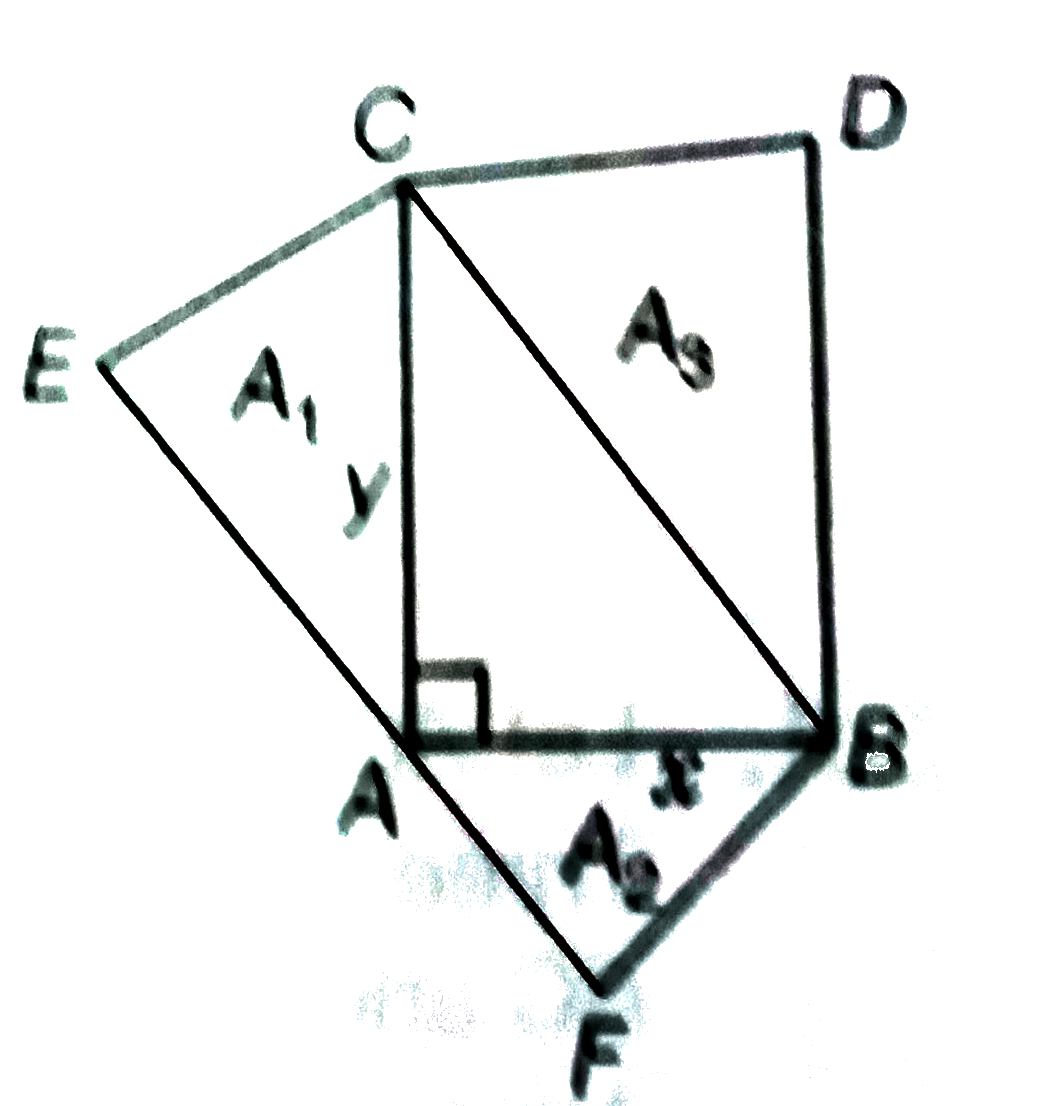
Let a right triangle BAC in which $∠ A$ is right angle and AC=y, AB=x
Three equilateral triangles $Δ A E C, Δ A F B and Δ C B D$ are drawn on the three sides of $Δ A B C$
Again let area of triangles made on AC,AB and BC are $A_{1}, A_{2} and A_{3}$ , respectively.
To prove $A_{3} = A_{1} + A_{2}$
Proof In $Δ C A B$ , by pythagoras theorem,
$B C^{2} = A C^{2} + A B^{2}$
$\Rightarrow B C^{2} = y^{2} + x^{2}$
$\Rightarrow B C = \sqrt{y^{2} + x^{2}}$
We know that, area of an equilateral triangle= $\frac{\sqrt{3}}{4} {(side)}^{\circ}$
$∴$ Area of equilateral $Δ A E C, A_{1} = \frac{\sqrt{3}}{4} {(A C)}^{2}$
$\Rightarrow A_{1} = \frac{\sqrt{3}}{4} y^{2}$
and equilateral $Δ A F B, A_{2} = \frac{\sqrt{3}}{4} {(A B)}^{2} = \frac{\sqrt{3}}{4} \sqrt{(y^{2} + x^{2})}$
$= \frac{\sqrt{3}}{4} (y^{2} + x^{2}) = \frac{\sqrt{3}}{4} y^{2} + \frac{\sqrt{3}}{4} x^{2}$
$= A_{1} + A_{2}$ [From Eqs (i) and (ii)]
Hence proved

Updated on:21/07/2023

The side of an equilateral triangle is 10 cm. Find its area (in $c m^{2}$ ).
A $10 \sqrt{3} c m^{2}$
B $25 \sqrt{3} c m^{2}$
C $50 \sqrt{3} c m^{2}$
D $75 \sqrt{3} c m^{2}$
The side (in cm) of a right triangle are $x - 1, x and x + 1$ .The area of triangle is
A $5 c m^{2}$
B $3 c m^{2}$
C $6 c m^{2}$
DNone of these