PYTHAGORAS THEOREM : In a Right angled triangle; the square of hypotenuse is equal to the sum of the squares of the other two sides.
Pythagoras Theorem
In this chapter, we will learn about Pythagoras Theorem. Students will be able to get a clear idea about the proof for Pythagoras Theorem and formula that would be easy to understand. Being the most fundamental theorems in mathematics, Pythagorean Theorem or Pythagoras Theorem defines the relationship between the three sides of the right-angled triangle.
According to the Pythagoras theorem, “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.” In this case, base, perpendicular and hypotenuse have been termed as the sides of the triangle. It is to be noted that the hypotenuse happens to be the longest side because it is opposite to the 900 angle. The values of a positive integer of the sides of a right-angled triangle are called the Pythagorean triple.
Pythagorean Theorem Formula
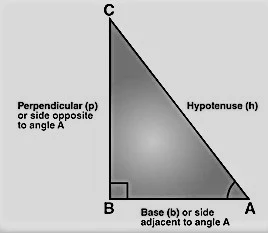
Suppose one of the legs on which the triangle rests as its base. Hypotenuse is the side that is opposite to the right angle. So, perpendicular is the remaining side. So, the Pythagorean theorem is mathematically represented as:
Hypotenuse2 = Perpendicular2 + Base2
Pythagorean Theorem Derivation
Here, let BD be the perpendicular to the side AC
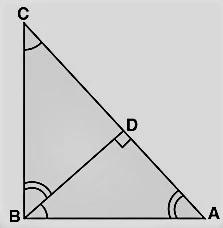
Look at the above figure where you can consider ΔABC and ΔADB,
In ΔABC and ΔADB
We can find ∠ABC =∠ADB=90°
∠A = ∠A → common
By making use of the AA criterion for the similarity of triangles,
We get ΔABC ≅ ΔADB
So, AD/AB = AB/AC
⇒ AB2 = AC x AD ……(1)
Now let us consider ΔABC and ΔBDC from the figure below:
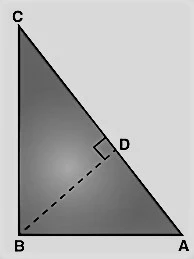
∠C = ∠C → common
Here, ∠CDB = ∠ABC = 90°
Now, by making use of the Angle Angle(AA) criterion for the similarity of triangles, we conclude that,
ΔBDC ≅ ΔABC
So, CD/BC = BC/AC
Therefore, BC2 = AC x CD …..(2)
From the similarity of triangles, we can conclude that,
Δ ADB ≅ ∠CDB = 90°
If we draw a perpendicular from the right-angled vertex of a right triangle to the hypotenuse, then there will be a triangle formed on both sides of the perpendicular. This would be similar to each other as well as to the whole triangle.
In order to prove AC2 =AB2 +BC2
We need to make the summation of equation (1) with equation (2) where we get:
AB2 + BC2= (AC x AD) + (AC x CD)
So, AB2 + BC2 = AC (AD+CD) …..(3)
We can find that AD+CD = AC, and so we substitute this value in equation (3)
Now, AB2 + BC2= AC (AC)
Therefore it becomes
AB2+ BC2= AC2
Hence, Pythagoras theorem is proved.
Now, we will look at some of the solved examples of Pythagoras theorem to get a good and clear understanding of it.
Related Videos:
- Similar Triangles and their properties
- Similar Polygons
- State and prove the Pythagoras theorem
- How similarity is different from congruence
Pythagorean Theorem Problems
Problem 1: The sides of a triangle are 7, 9 & 12 units. Find out whether it is a right angle or not.
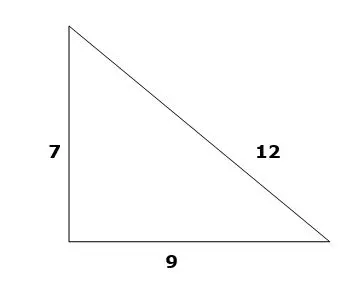
Solution: From Pythagoras Theorem, we have;
Perpendicular2 + Base2 = Hypotenuse2
Perpendicular = 7 units
Base = 9 units
Hypotenuse = 12 units
72 + 92 = 122
⇒ 49 + 81 = 144
⇒ 130 = 144
L.H.S. = R.H.S.
Therefore, the angles opposite to the 12 unit side cannot be a right angle.
Problem 2
In the figure below, the two sides of a right angled has been shown. Can you find out the third side?
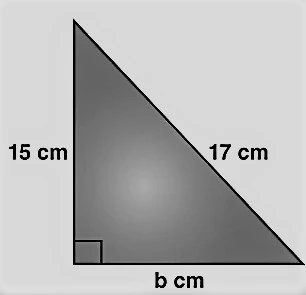
Solution: Given;
Perpendicular = 15 cm
Base = b cm
Hypotenuse = 17 cm
As per the Pythagorean Theorem, we have;
Perpendicular2 + Base2 = Hypotenuse2
⇒ 152 + b2 = 172
⇒ 225 + b2 = 289
⇒ b2 = 289 – 225
⇒ b2 = 64
⇒ b = √64
Therefore, b = 8
Problem 3: In the figure below, the sides of a square are 4 cm. Can you find the length of the diagonal?
Solution- Given;
Sides of a square = 4 cm
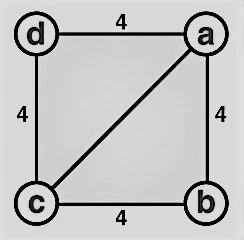
What To Find - The length of diagonal ac.
Let us consider triangle abc or acd
(ab)2 + (bc)2 = (ac)2
(4)2 + (4)2 = (ac)2
16 + 16 = (ac)2
32 = (ac)2
(ac)2 = 32
or ac = 4√2.
Therefore, the length of the diagonal is 4√2.
Problem 4: In the below figure, you can find the two sides of 3 cm and 4 cm. Find out the length of the hypotenuse.
Solution: Let the length of the hypotenuse = c
Here, a =3 and b = 4
Now, we apply the formula, which is:
a2 + b2 = c2
⇒ 32 + 42 = c2
⇒ 9 + 16 = c2
⇒ 25 = c2
⇒ √25 = c2
⇒ 5 = c
Now, we will check this answer to verify:
32 + 42 = 52
⇒ 9 + 16 = 25
⇒ 25 = 25
Therefore, we can conclude that the length of the hypotenuse is 5.
Important Chapters:







Similar Questions
Theorem 6.8 : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
View SolutionProve that is a right angle triangle, the square of the hypotenuse is equal the sum of the squares of other two sides.
View Solution(Pythagoras's Theorem) Prove by vector method that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
View Solution(Pythagoras’s Theorem) Prove by vector method that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
View SolutionProve that, in a right-angled triangle, the square of hypotenuse is equal to the sum of the square of remaining two sides.
View SolutionSTATEMENT In a right triangle the square of the hypotenuse equals the sum of the squares of its remaining two sides.
View SolutionProve that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Use the above theorem, in the following.
If ABC is an equilateral triangle with AD⊥BC, then prove that AD2=3DC2.
View SolutionIn order to prove, 'In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of remaining two sides
(i) Draw a near labelled figure.
(ii) Write 'Given' and 'To Prove' from the figure drawn by you.
View SolutionIn aright angled triangle, the square of the hypotenuse is equal to to the sum of squares on the other two sides, prove. Using the above theorem, determine the length of AD in terms of b and c.
View SolutionIn a right-angled triangle, the square of hypotenuse is equal to the sum of the squares of the two sides. Given that ∠B of △ABC is an acute angle and AD⊥BC . Prove that AC2=AB2+BC2−2BC.BD.
View Solution

