In the figure , ABC is triangle in which ∠ABC<90∘andAD⊥BC. Prove that AC2=AB2+BC2−2BC⋅BD.
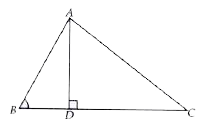
The correct Answer is:=AB2+BC2−2BC⋅BD
Step by step video, text & image solution for In the figure , ABC is triangle in which angleABClt90^(@)andADbotBC. Prove that AC^(2)=AB^(2)+BC^(2)-2BC*BD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Multiple Choice Questions) (LEVEL -1 )
35 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Multiple Choice Questions) (LEVEL -2)
15 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.5
21 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
In figure, ∠B<90∘andAD⊥BC. Prove that AC2=AB2+BC2−2BC.BD
View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
View SolutionIn a ABC , ∠ABC=135o . Prove that AC2=AB2+BC2+4 ar(ABC)
View SolutionIn a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2
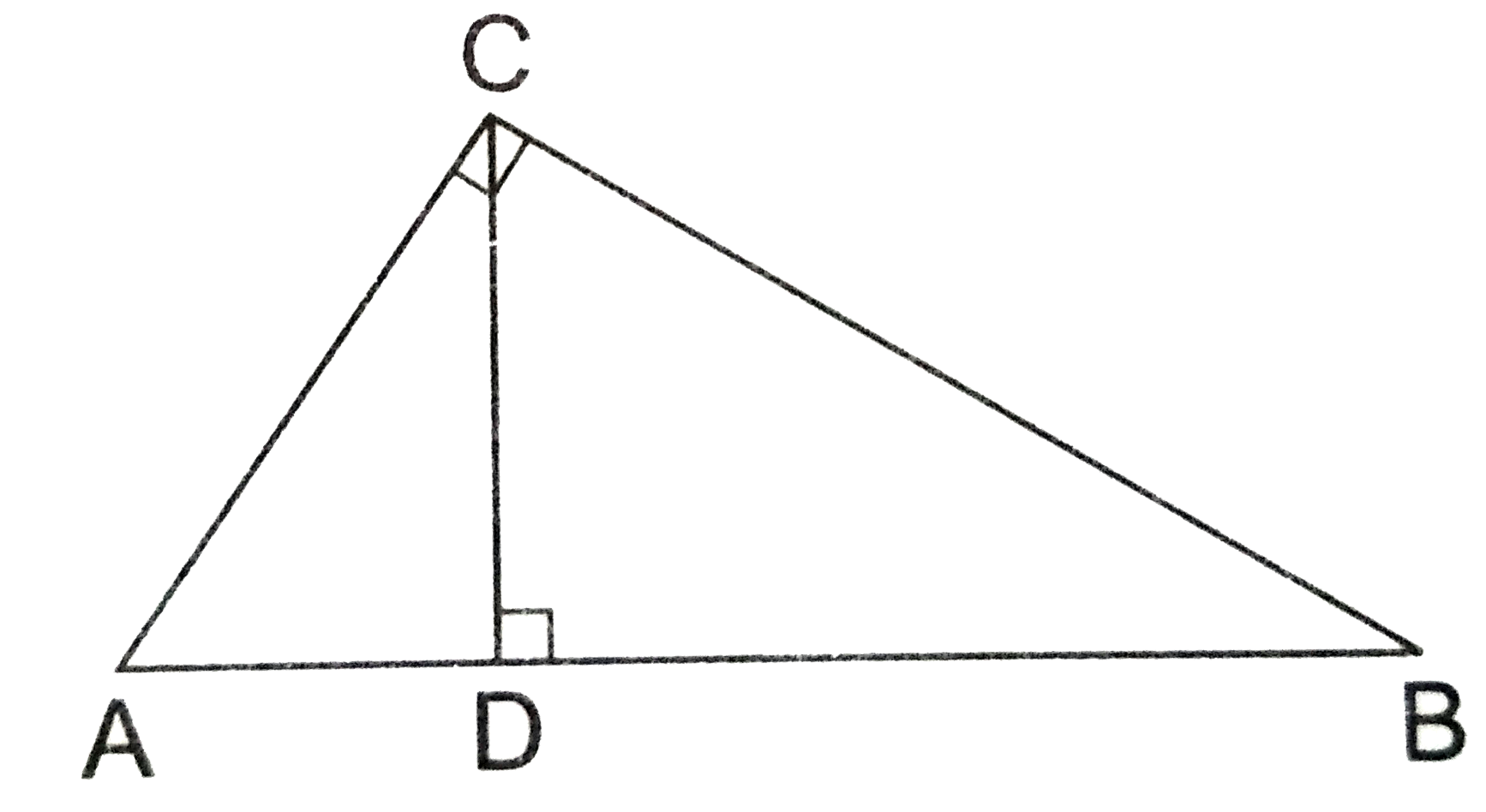
View SolutionIn the given figure ∠ABC=90∘andCD⊥AB. Prove that BC2AC2=BDAD
View SolutionIn a right-angled triangle, the square of hypotenuse is equal to the sum of the squares of the two sides. Given that ∠B of △ABC is an acute angle and AD⊥BC . Prove that AC2=AB2+BC2−2BC.BD.
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that

AB2=BC×BD
View Solution(Result on acute triangle) In Fig. 4.184, ∠B of ABC is an acute angle and AD⊥BC , prove that AC2=AB2+BC2−2 BC×BD
View Solutionin ΔABC,∠A=2∠B Prove that BC2=AC2+AC.AB
View SolutionIn a triangle ABC,B=90∘ and D is the mid-point of BC then prove that AC2=AD2+3CD2
View Solution
