In Fig. 4.121, ABC is a right triangle right angled at B and D is the foot of the the perpendicular drawn from B on AC . If DM⊥BC and DN⊥AB , prove that: (FIGURE) DM2=DN×MC (ii) DN2=DM×AN
The correct Answer is:(i) =DN×MC
(ii) =DM×AN
Step by step video, text & image solution for In Fig. 4.121, A B C is a right triangle right angled at B and D is the foot of the the perpendicular drawn from B on A C . If D M_|_B C and D N_|_A B , prove that: (FIGURE) D M^2=D NxxM C (ii) D N^2=D MxxA N by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise: Exercise (Multiple Choice Questions) (LEVEL -1 )
Explore 35 Videos
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise: Exercise (Multiple Choice Questions) (LEVEL -2)
Explore 15 Videos
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise:NCERT Section Exercise 6.5
Explore 21 Videos
- SURFACE AREAS AND VOLUMESBook:MTG IIT JEE FOUNDATIONChapter:SURFACE AREAS AND VOLUMESExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
Similar Questions
In fig., D is a point on hypotenuse AC of ΔABC,DM⊥BCand DN⊥AB. Prove that
(i) DM2=DN⋅MC
(ii) DN2=DM⋅AN

View SolutionIn fig.41, ABC is a right triangle right angled at A. D lies on BA produced and DE⊥BC, intersecting AC at F . if ∠AFE=1300, find ∠BDE (ii) ∠BCA ∠ABC
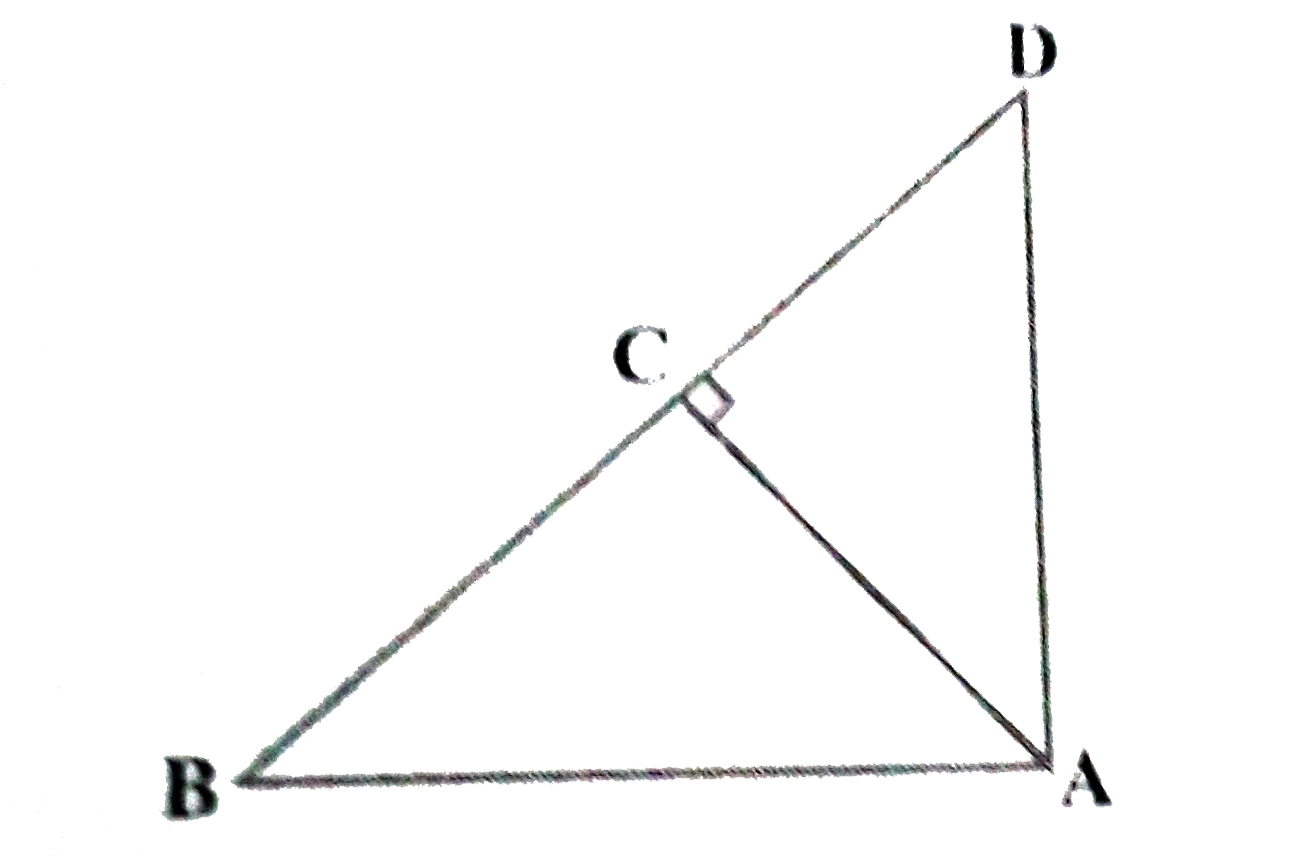
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
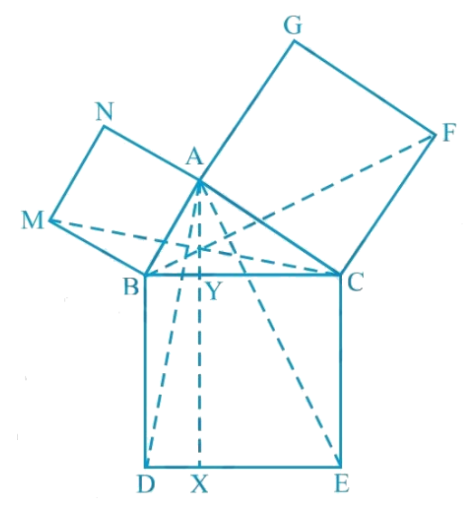
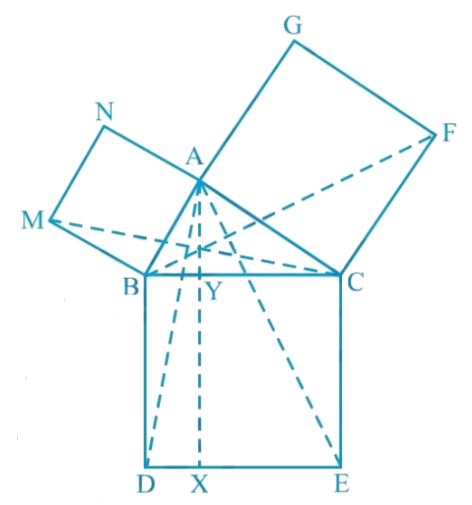
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: FCB≅ ACE
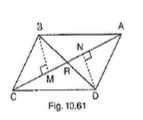
View SolutionIn Figure, BM and DN are both perpendiculars to the segments AC and BM=DN . Prove that AC bisects BD
View SolutionABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar(CYXE)=ar (ACFG)
View SolutionIn Fig. 5.10, if AC=BD, then prove that AB=CD.

View SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=90∘ (iii)DBC≅ACB (iv) CM=12AB
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=2 ar ( MBC)
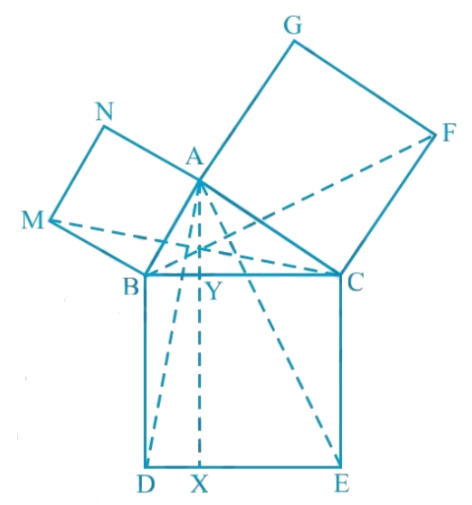
View Solution
