If perpendiculars from any point with an angle on its arms are congruent, prove that it lies on the bisector of that angle.
Video Solution
Text Solution
To prove-∠1=∠2
Proof-In∠PMBand∠PMB
PM=PN(given)
BP=BD(common)
∠PMB=∠PNB(each90∘)
∠PMB≅∠PNB(RHS)
∠1=∠2
BP bisects ∠B.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The point of intersection of the angle bisectors of a triangle is :
AorthocentreBcentroidCincentreDcircumcentreThe point of intersection of the angle bisectors of a triangle is :
AorthocentreBcentroidCincentreDcircumcenter
Two acute angles are congruent
View SolutionCongruent angles
View SolutionProve that, angles inscribed in the same are arc congruent.

View SolutionIn any triangle ABC, if the angle bisector of ∠Aand perpendicular bisector of BCintersect, prove that they intersect on the circumcircle of the triangle ABC
View SolutionLine l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
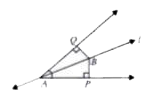
BP=BQ or B is equidistant from the arms of ∠A.
View SolutionProve that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
View Solution