In any triangle ABC, if the angle bisector of ∠Aand perpendicular bisector of BCintersect, prove that they intersect on the circumcircle of the triangle ABC
Video Solution
Text Solution
Angle bisector∠Ameets the circumcircle of triangleABC at point P
from diagram
∠BAD=∠CAD
so, ABD is a Cyclic Quadrilateral
∠DBC=∠DAC=12∠A
∠DCB=∠BAD=12∠A
∠DBC=∠DCB
In△DCB
BP and CD are equal
D lies on perpendicular bisector of BC
|
Topper's Solved these Questions
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - Exercise 10.1
2 Videos
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - Solved Examples
6 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 9.1
1 Videos
- CONSTRUCTIONSBOOK - NCERTCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.2
5 Videos
Similar Questions
Knowledge Check
In a triangle, with usual notations, the length of the bisector of angle A is
A2bcb+csinA2B2bcb+ccosA2Cabc2R(b+c)cosecA2D4Ab+ccosecA2In given triangle ABC ,AP is bisector of ∠BAC and AQ is perpendicular to BC then ∠PAQ is equal to
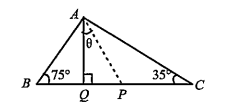 A20∘B40∘C15∘D25∘
A20∘B40∘C15∘D25∘The point of intersection of the angle bisectors of a triangle is :
AorthocentreBcentroidCincentreDcircumcentre
If in a triangle ABC,CD is the angular bisector of the angle ACB then CD is equal to
View SolutionIn a triangle ABC with ∠BCA=90∘, the perpendicular bisector of AB intersects segments AB and AC at X and Y, respectively. If the ratio of the area of quadrilateral BXYC be the area of triangle ABC is 13:18 and BC=12 then which is the length of AC?
View SolutionProve that the internal bisectors of the angles of a triangle are concurrent
View SolutionIn a triangle ABC, the bisector of angle A meets the opposite side at D. Using vectors prove that BD:DC=c:b.
View SolutionThe point of intersection of the angle bisectors of a triangle is :
View Solution
