ABCD is a square, X and Y are points on sides AD and BC respectively such that AY=BX. Prove that BY=AX and .
Given:
is a square
To prove:
Proof: In and
(common)
(given)
( each)
By
Hence Proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, ABCD is a square. E and Fare midpoints of AD and BC respectively. The ratio of areas of ΔGAB and ΔHAB
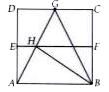 A4 : 1B1 : 4C1 : 2D2 : 1
A4 : 1B1 : 4C1 : 2D2 : 1
ABCD is a parallelogram. Tow points P and Q are taken on sides AD and BC respectively such that AP 13ADandCQ=13BC. Prove that □AQCP is a parallelogram.
View SolutionABCD is a square. P, Q, R, S are points on the sides AB. BC, CD, DA respectively such that AP = BQ = CR = DS. What is ∠SPQ equal to ?
View SolutionK, L, M and N are points on the sides AB, BC, CD and DA respectively of a square ABCD such that AK = BL = CM = DN. Prove that KLMN is a square.
View SolutionIn the adjoining figure, ABCD is a quadrilateral. M and N are the points on AD and CD respectively such that AB=BC,∠ABM=∠CBN and ∠MBD=∠NBD. Prove that BM=BN.

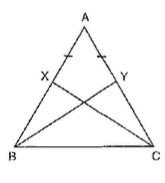
View SolutionIn the adjoining figure, X and Y are respectively two points on equal sides AB and AC of ΔABC such that AX = AY. Prove that CX = BY.
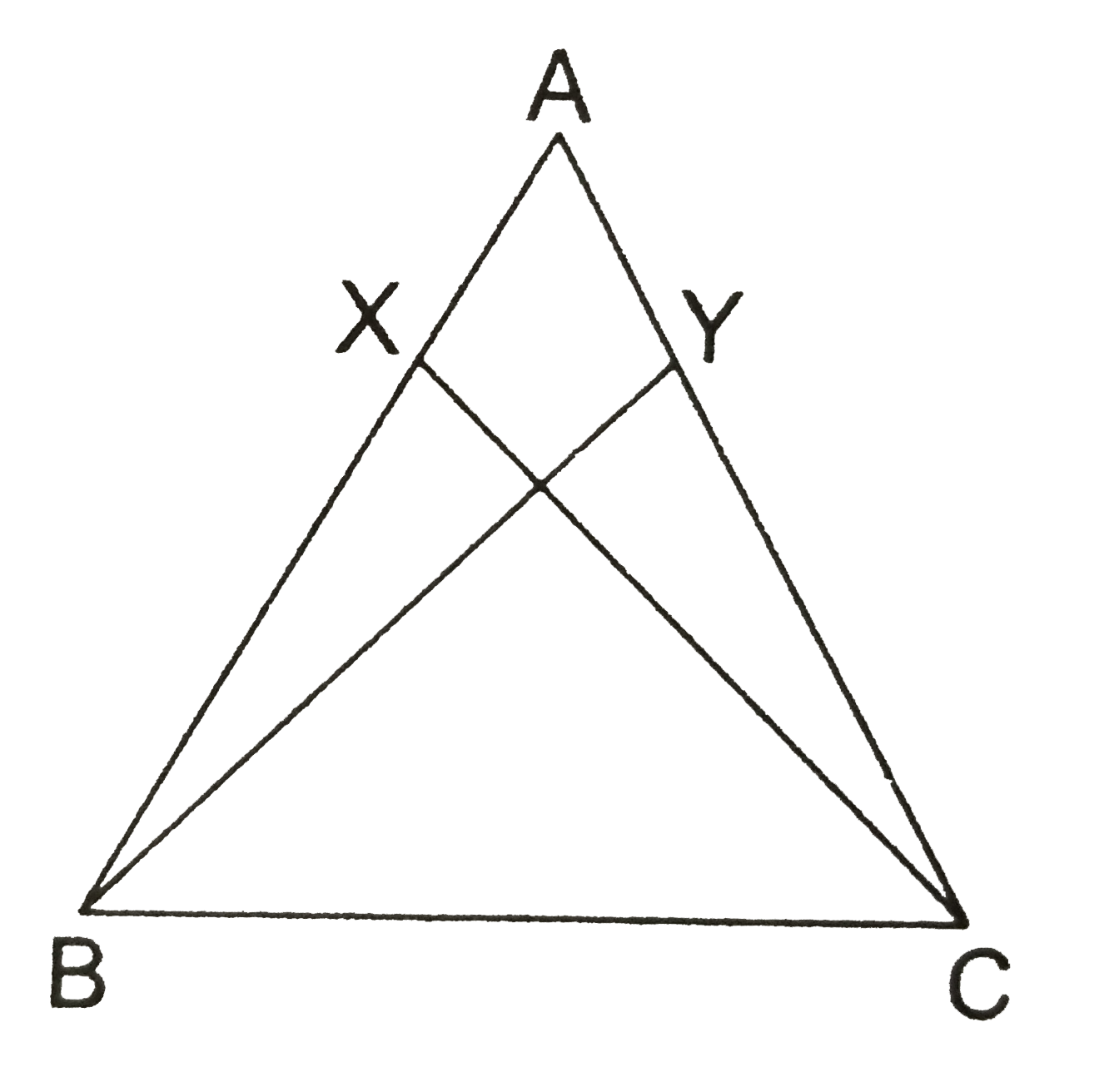
View SolutionIn the adjoining figure, X and Y are respectively two points on equal sides AB and AC of ΔABC such that AX=AY. Prove that CX=BY.
View SolutionIn a triangle ABC,XandY are the points on ABandBC respectively. If BX=12ABandBY=12BCandAB=BC. Show that BX=BY.
View Solution