In the adjoining figure, ABCD is a quadrilateral. M and N are the points on AD and CD respectively such that AB=BC,∠ABM=∠CBN and ∠MBD=∠NBD. Prove that BM=BN.

Step by step video & image solution for In the adjoining figure, ABCD is a quadrilateral. M and N are the points on AD and CD respectively such that AB = BC, angleABM=angleCBN and angleMBD=angleNBD. Prove that BM = BN. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Exercise 7b
Explore 15 Videos
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Revision Exercise (very Short Answer Questions)
Explore 10 Videos
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Problems From NCERT/exemplar
Explore 5 Videos
- SURFACE AREA AND VOLUMEBook:NAGEEN PRAKASHANChapter:SURFACE AREA AND VOLUMEExercise:Revision Exercise (long Answer Questions)
Explore 10 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
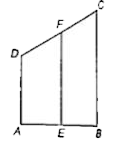 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
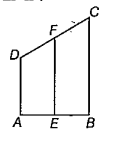
ABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral.If side BC is produced upto point E and ∠DAB=95∘, then find the value of ∠DCE.

View SolutionIn the given figure ABCD is, ABCD is a quadrilateral in which AB∣∣DC and AD∣∣BC prove that ANGLEADC=ANGLEABC.

View SolutionK, L, M and N are points on the sides AB, BC, CD and DA respectively of a square ABCD such that AK = BL = CM = DN. Prove that KLMN is a square.
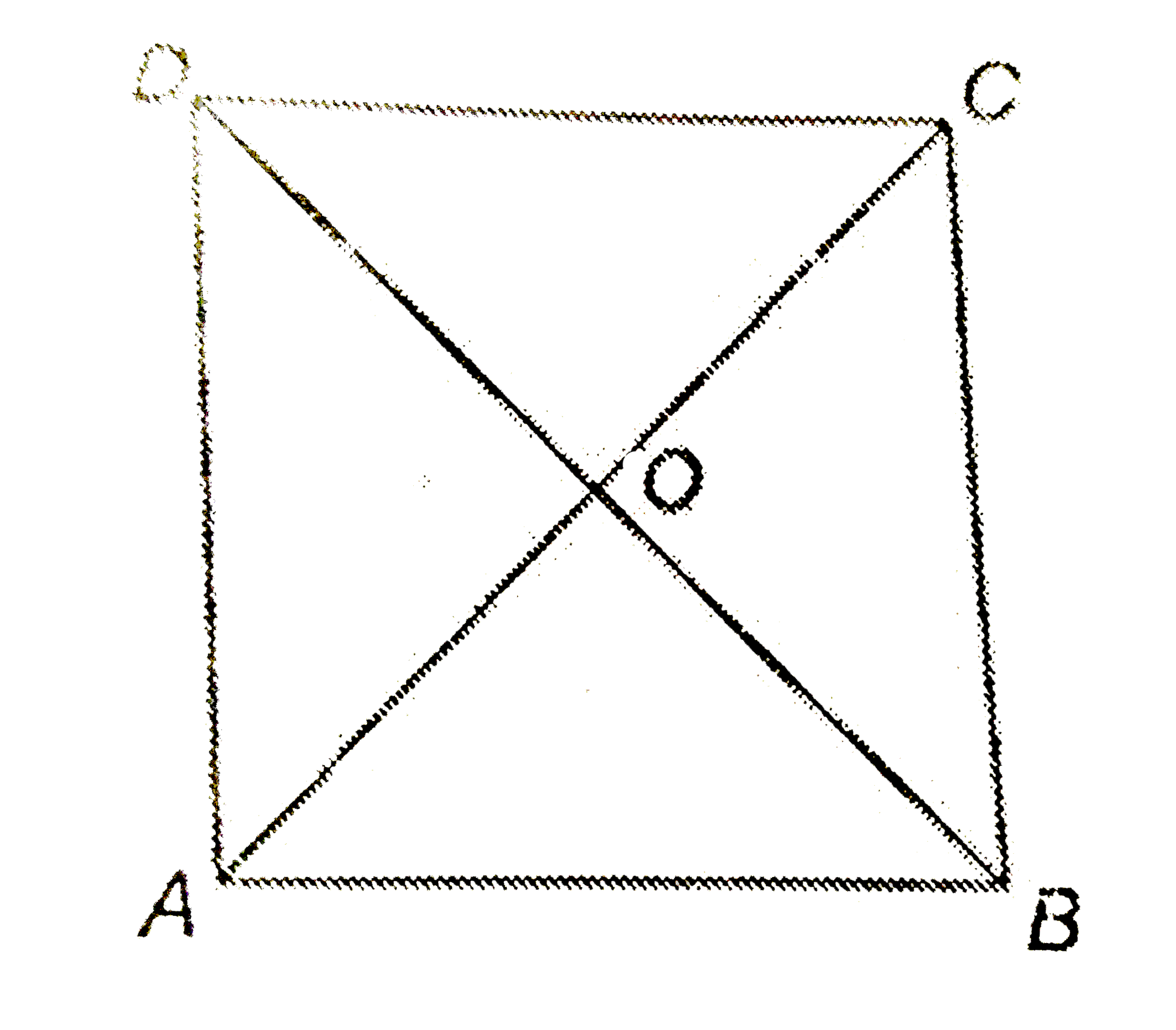
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)
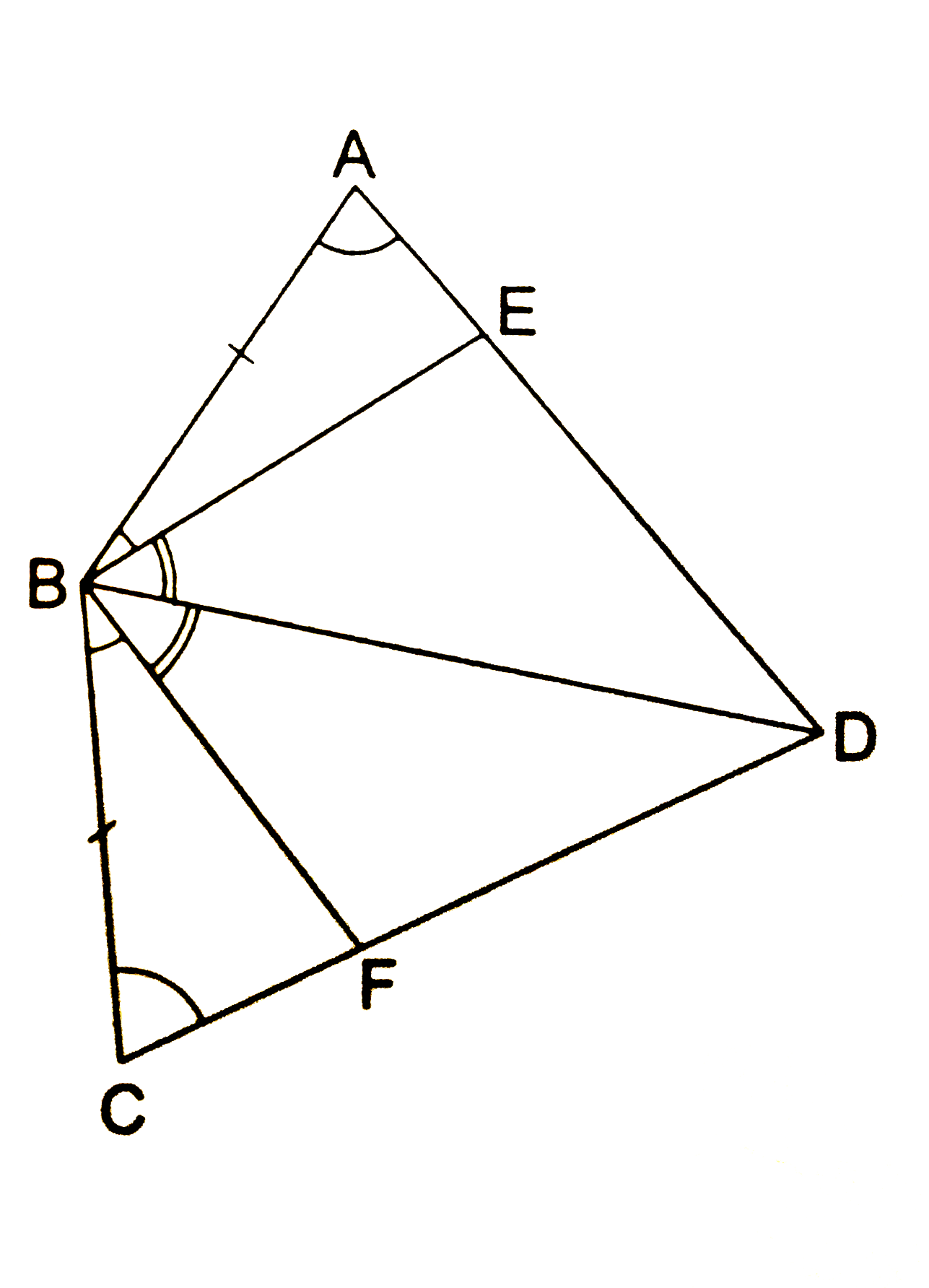
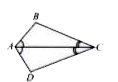
View SolutionIn the figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.
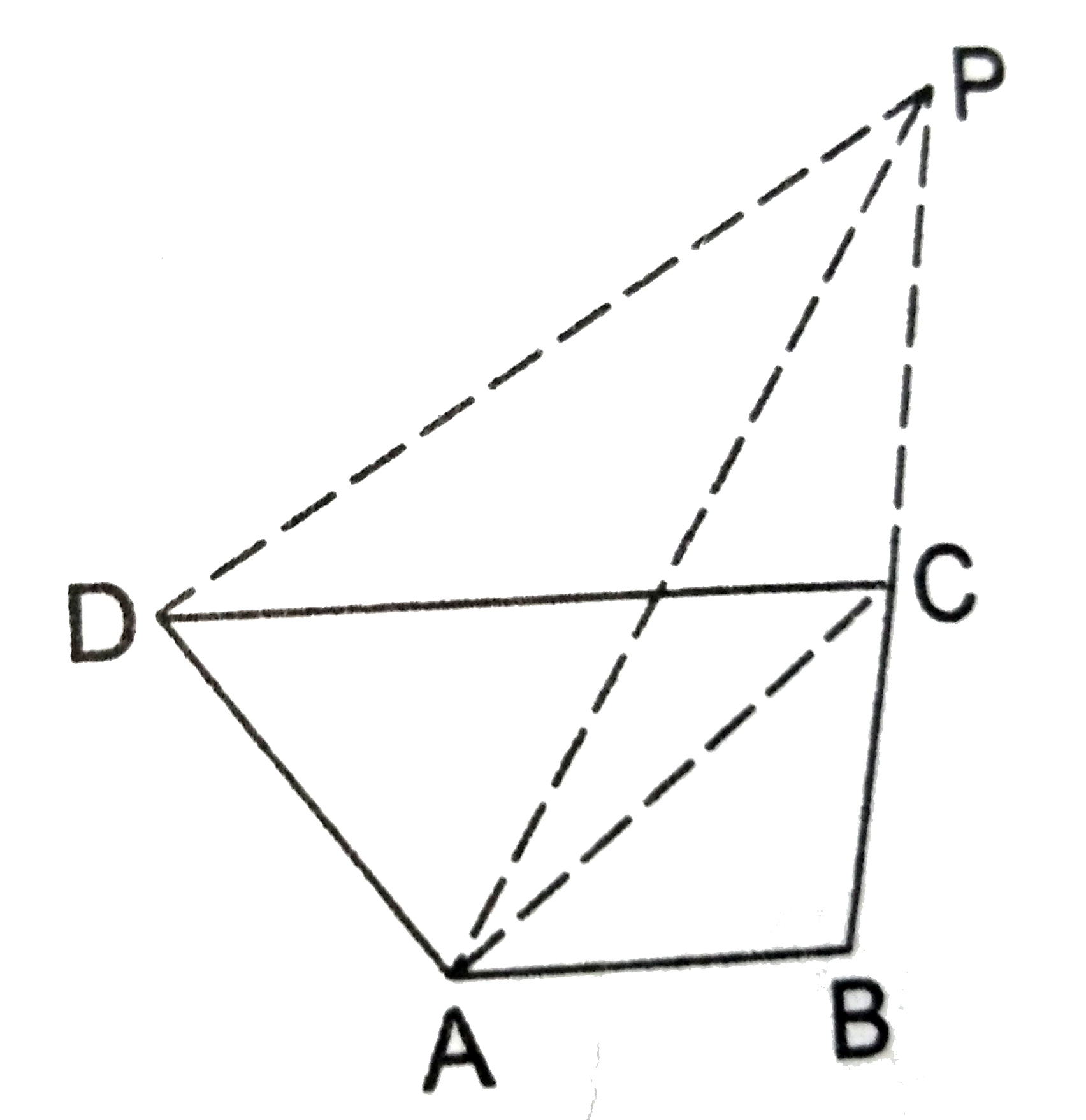
View SolutionIn the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that ar(△ABP)=ar(qaud. ABCD).
View Solution