In cm, cm and cm. find the largest angle.
None of these
The correct Answer is:C
To find the largest angle in triangle ABC, we can use the property that the largest angle is opposite the longest side. Here are the steps to solve the problem:
Step 1: Identify the lengths of the sides
We have the following sides:
- AB = 8 cm
- BC = 15 cm
- AC = 17 cm
Step 2: Determine the longest side
Among the sides AB, BC, and AC, we can see that:
- AB = 8 cm
- BC = 15 cm
- AC = 17 cm
The longest side is AC, which measures 17 cm.
Step 3: Identify the angle opposite the longest side
The angle opposite the longest side (AC) is angle B. Therefore, angle B is the largest angle in triangle ABC.
Step 4: Use the cosine rule to find angle B
We can use the cosine rule to find the measure of angle B. The cosine rule states that:
c2=a2+b2−2ab⋅cos(C)
where C is the angle opposite side c.
In our case:
- a=AB=8 cm
- b=BC=15 cm
- c=AC=17 cm
Plugging in the values:
172=82+152−2⋅8⋅15⋅cos(B)
Step 5: Calculate the squares of the sides
Calculating the squares:
- 172=289
- 82=64
- 152=225
Now substitute these values into the equation:
289=64+225−2⋅8⋅15⋅cos(B)
Step 6: Simplify the equation
Combine the terms on the right:
289=289−240⋅cos(B)
Step 7: Isolate cos(B)
Subtract 289 from both sides:
0=−240⋅cos(B)
This simplifies to:
240⋅cos(B)=0
Step 8: Solve for cos(B)
Dividing both sides by 240 gives:
cos(B)=0
Step 9: Find angle B
The angle for which the cosine is 0 is:
B=90∘
Conclusion
Thus, the largest angle in triangle ABC is 90∘.
---
We have the following sides:
- AB = 8 cm
- BC = 15 cm
- AC = 17 cm
Among the sides AB, BC, and AC, we can see that:
- AB = 8 cm
- BC = 15 cm
- AC = 17 cm
The angle opposite the longest side (AC) is angle B. Therefore, angle B is the largest angle in triangle ABC.
We can use the cosine rule to find the measure of angle B. The cosine rule states that:
c2=a2+b2−2ab⋅cos(C)
where C is the angle opposite side c.
- a=AB=8 cm
- b=BC=15 cm
- c=AC=17 cm
172=82+152−2⋅8⋅15⋅cos(B)
Calculating the squares:
- 172=289
- 82=64
- 152=225
289=64+225−2⋅8⋅15⋅cos(B)
Combine the terms on the right:
289=289−240⋅cos(B)
Subtract 289 from both sides:
0=−240⋅cos(B)
240⋅cos(B)=0
Dividing both sides by 240 gives:
cos(B)=0
The angle for which the cosine is 0 is:
B=90∘
Thus, the largest angle in triangle ABC is 90∘.
Topper's Solved these Questions
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Revision Exercise (very Short Answer Questions)
Explore 10 Videos
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Revision Exercise (short Answer Type Question)
Explore 10 Videos
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Exercise 7a
Explore 35 Videos
- SURFACE AREA AND VOLUMEBook:NAGEEN PRAKASHANChapter:SURFACE AREA AND VOLUMEExercise:Revision Exercise (long Answer Questions)
Explore 10 Videos
Similar Questions
Knowledge Check
In a △ABC,AB = 10 cm, BC = 12 cm and AC = 14 cm. Find the length of median AD. If G is the centroid, find length of GA.
A53√7,59√7B5√7,4√7C10√3,83√7D4√7,83√7In a ΔABC, BC = 9 cm, AC = 40 cm and AB = 41 cm. If bisector of angle A meets side BC at D then ratio of area of ΔABD and ΔABC is
A41:40B9:40C9:41D41:81In Δ ABC, AB = 6 cms, BC = 10 cms, AC = 8cm and ADI_BC. Find the value of the ratio of BD:DC.
A3:4B9:16C4:5D16:25
If in ΔABC AB =15 cm,BC = 17 cm and AC = 8 cm then which of the following will be a right angle?
View SolutionIn a ΔABC , AB = 5, AC = 6cm, BC = 8 cm. Find the lengh of median AD.
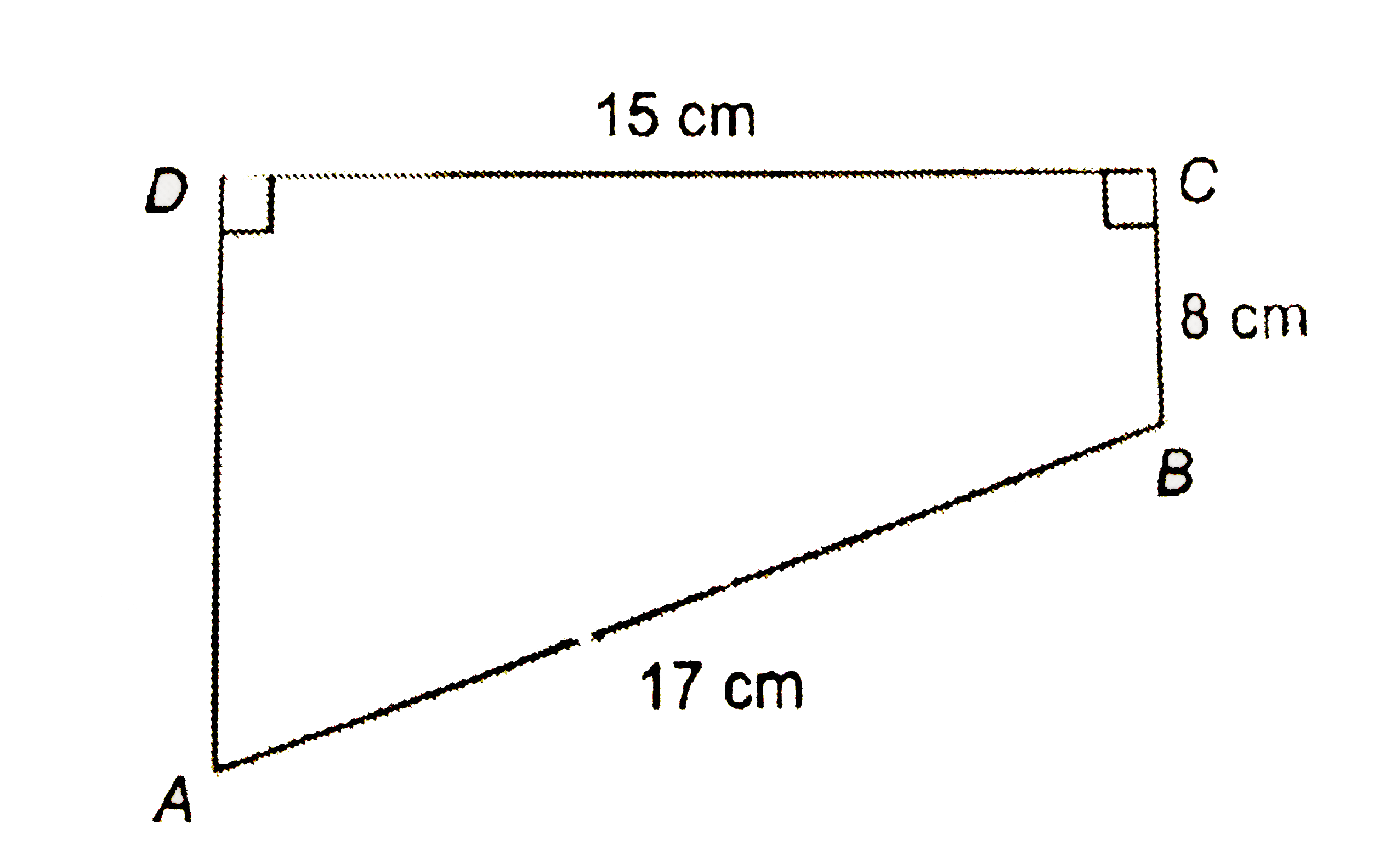
View SolutionThe given figure shows a trapezium ABCD in which AB = 17 cm, BC = 8 cm and CD = 15 cm. Find the area of the trapezium.
View SolutionIn fig.45, ABC,AB=3cm,BC=4cm and AC=5cm. name the smallest and the largest angles of the triangle.
View SolutionIn ΔABC,AB=6√3cm,AC=12cm,BC=6cm. Find measure of ∠A.
View Solution

