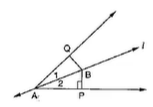
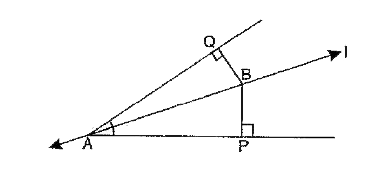
In Figure, line l is the bisector of angle A and B is any point on l . BP and BQ are perpendiculars from B to the arms of A. Show that : APB≅AQB BP=BQ or B is equidistant from the arms of ∠A . Figure
Given- ∠1=∠2
In∠AQBand∠APB
∠1=∠2(given)
AB=AB(common)
∠BQA=∠BPA(each 90)
∠AQB≅∠APB(AAS)
BQ=BP.
Topper's Solved these Questions
Similar Questions
In Figure, line l is the bisector of angle A and B is any point on l.BP and BQ are perpendiculars from B to the arms of A. Show that: APB ≅AQB BP=BQ or B is equidistant from the arms of ∠A
View Solutionline l is the bisector of an angle ∠A and∠Bis any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A

View SolutionLine l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
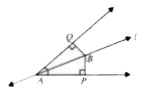
ΔAPB≅ΔAQB
View SolutionIn the given figure, line l is the bisector of an angle ∠A and B is any point on l. If BP and BQ are perpendiculars from B to the arms of ∠A, show that
(i) ΔAPB≅ΔAQB
(ii) BP = BQ, i.e., B is equidistant from the arms of ∠A.
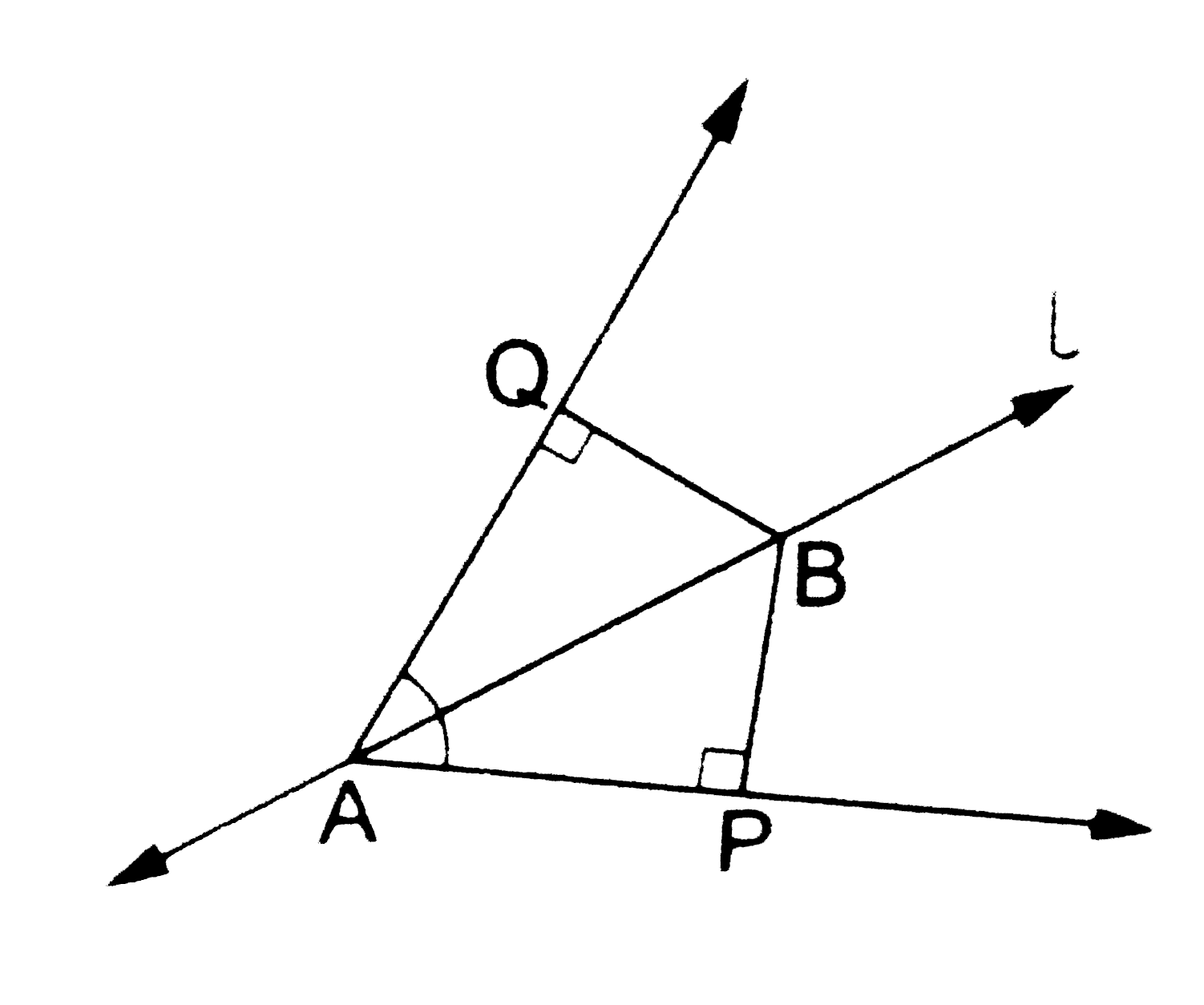
View SolutionLine l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
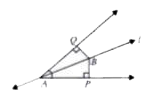
BP=BQ or B is equidistant from the arms of ∠A.
View SolutionIn the given figure, line I is the bisector of an angle A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A. Show that B is equidistant from the arms of ∠A.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
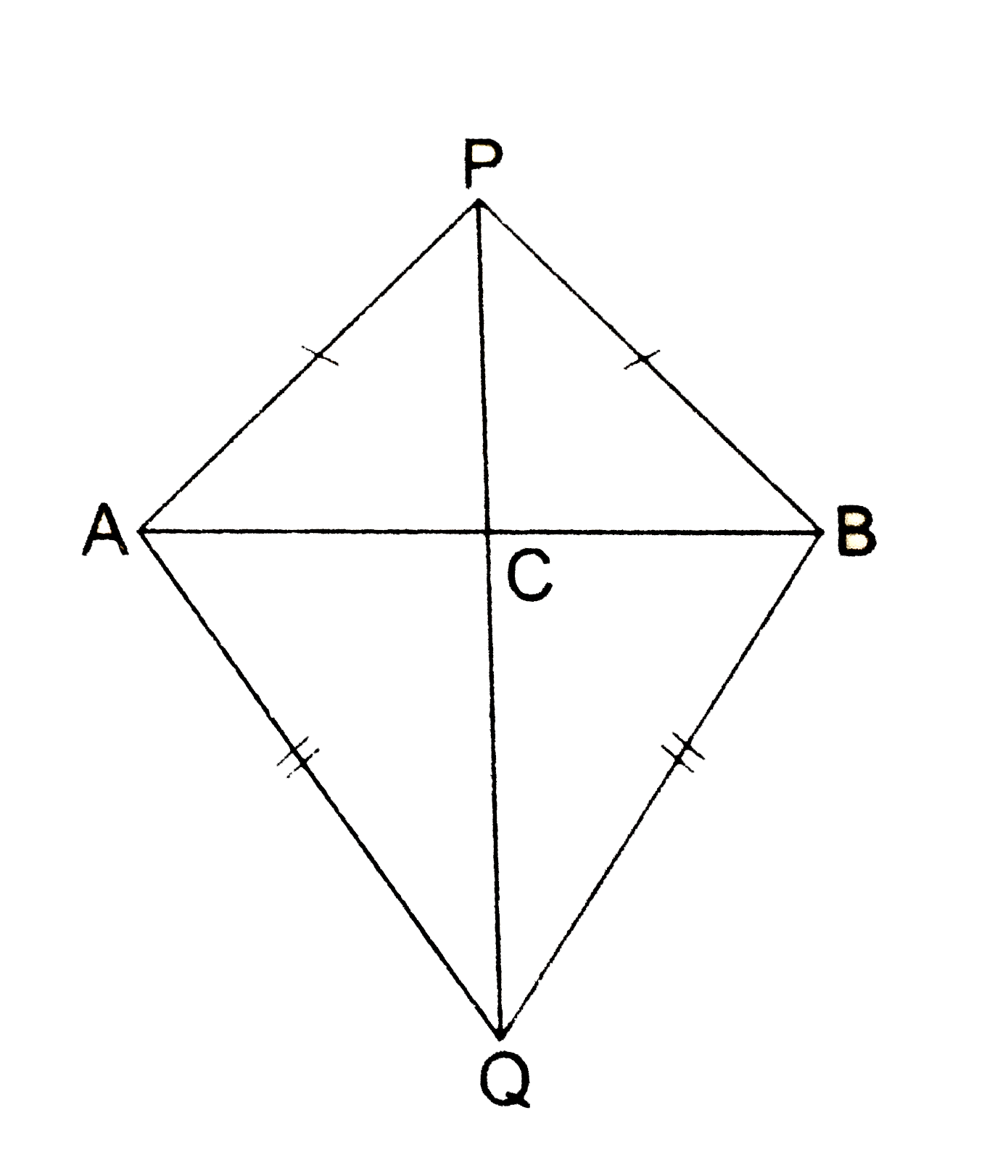
View SolutionIn the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
View Solution
