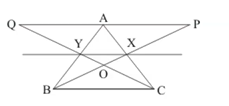
In ABC and PQR Figure, AB=PQ,BC=QR and CB and RQ are extended to X and Y respectively and ∠ABX =∠PQY. Prove that ABC≅PQR. Figure
In ΔABC and ΔPQR
AB=PQ and BC=QR
CB and RQ extended to X and Y.
∠ABX=∠PQY
∠ABC=180∘−∠ABX=180∘=∠PQY
∠PQR=180∘−∠PQY=∠ABC
We get in both triangles,
AB=PQ
BC=QR
∠ABC=∠PQR
Then both triangle are congruent, i.e. ΔABC≅ΔPQR.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the pth, qth and rth terms of a G.P. be respectively , a,b and c then the value of aq−r.br−p.cp−q is :
A0B1C3Dabc//pqr
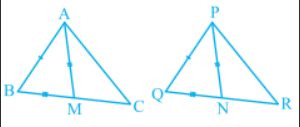
In Figure, two sides AB and BC and the median AD of ABC are equal respectively to the two sides PQ and QR and the median PM of the other triangle PQR. Prove that ABD≅PQM (ii) ABC ≅ PQR
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionIf ABC≅PQR and ABC is not congruent to RPQ, then which of the following not true: BC=PQ (b) AC=PR (c) AB=PQ (D) QR=BC
View SolutionIf the pth, qth and rth terms of a G.P. are a,b and c, respectively. Prove that
aq−rbr−pcp−q=1.
View Solution