line l is the bisector of an angle ∠A and∠Bis any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A

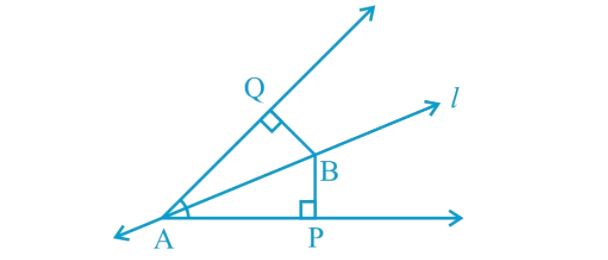
Given: l is the bisector of an angle ∠A and BP⊥AP and BQ⊥AQ
To Prove: ΔAPB≅ΔAQBand BP=BQ
i) We can show two triangles APB and AQB are congruent by using AAS congruency rule and then show that the corresponding parts of congruent triangles will be equal.
In ΔAPB and ΔAQB,
∠BAP=∠BAQ (l is the angle bisector of ∠A)
∠APB=∠AQB (Each 90∘)
AB=AB (Common)
∴ΔAPB≅ΔAQB (By AAS congruence rule)
ii) Since ΔAPB≅ΔAQB
∴BP=BQ(By CPCT)
Or, it can be said that point B is equidistant from the arms of ∠A.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.8
10 Videos
Similar Questions
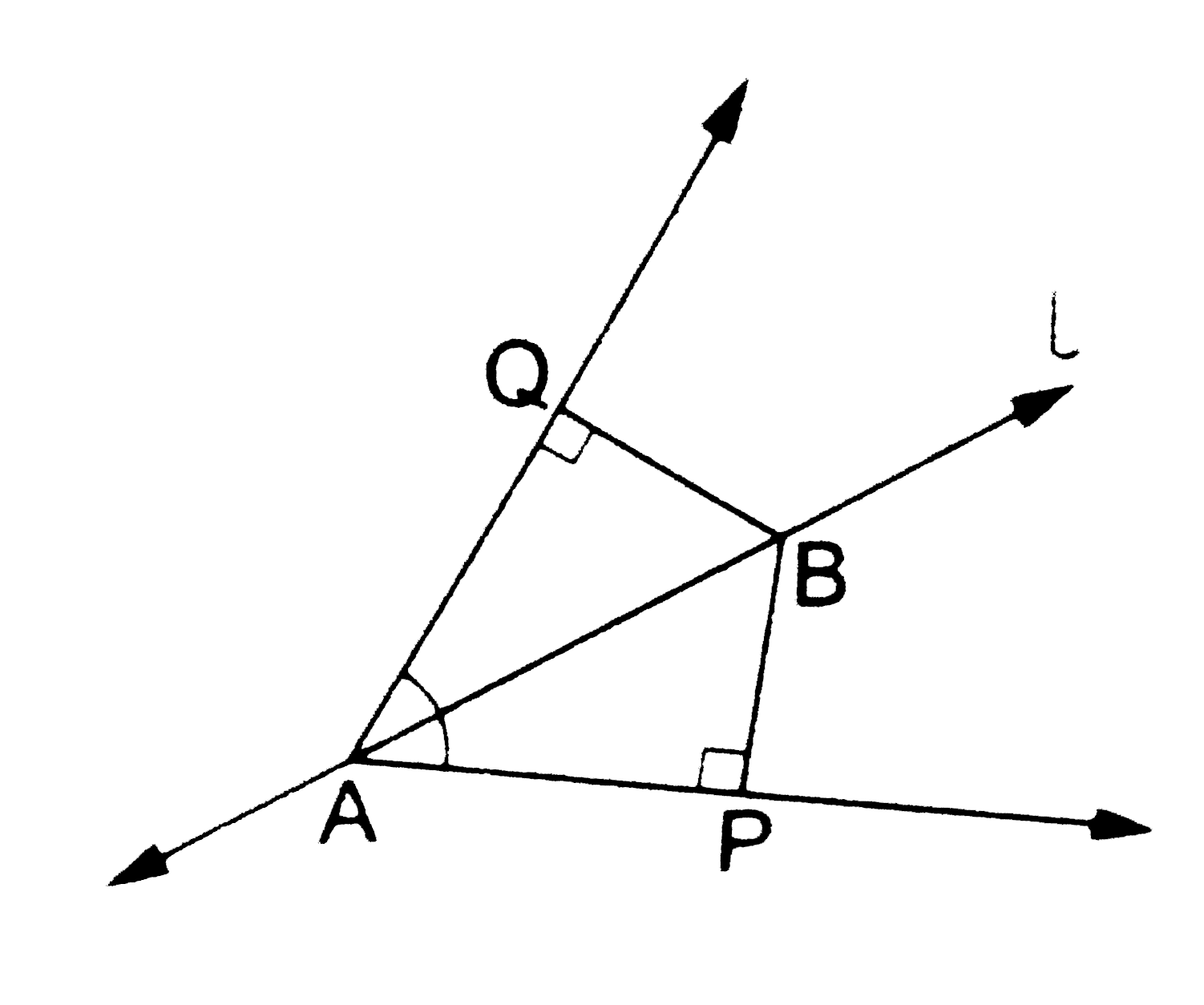
In the given figure, line l is the bisector of an angle ∠A and B is any point on l. If BP and BQ are perpendiculars from B to the arms of ∠A, show that
(i) ΔAPB≅ΔAQB
(ii) BP = BQ, i.e., B is equidistant from the arms of ∠A.
View SolutionLine l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
ΔAPB≅ΔAQB
View Solution
Knowledge Check
In ΔABC,∠B=60∘,∠C=40∘,ADis the bisector of ∠AandAE is drawn perpendicular on BC from A. Then the measure of ∠EADIS
A40∘B30∘C10∘D80∘In a △ABC, the bisectors of ∠B and ∠C meets at point O inside the triangle. If ∠BOC=122∘, then the measure of ∠A
△ABCमें, ∠B तथा ∠C द्विभाजक त्रिभुज के भीतर बिंदु O पर मिलते हैं | यदि ∠BOC=122∘ है, तो ∠A का माप क्या होगा ?A64∘B62∘C72∘D68∘
In Figure, line l is the bisector of angle A and B is any point on l . BP and BQ are perpendiculars from B to the arms of A. Show that : APB≅AQB BP=BQ or B is equidistant from the arms of ∠A . Figure
View SolutionIn Figure, line l is the bisector of angle A and B is any point on l.BP and BQ are perpendiculars from B to the arms of A. Show that: APB ≅AQB BP=BQ or B is equidistant from the arms of ∠A
View SolutionLine l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
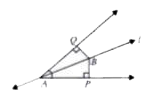
BP=BQ or B is equidistant from the arms of ∠A.
View SolutionIn the given figure, line I is the bisector of an angle A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A. Show that B is equidistant from the arms of ∠A.
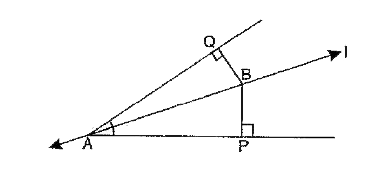
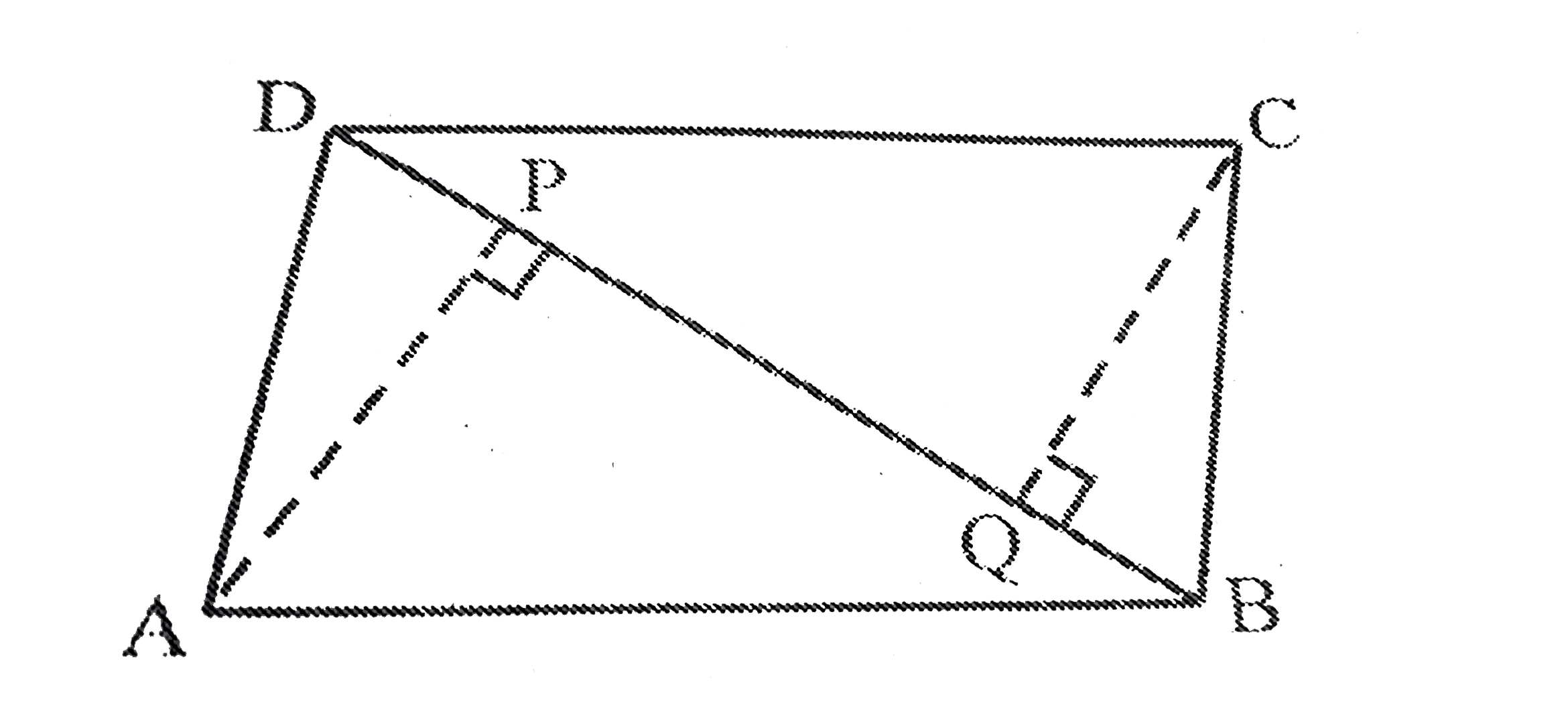
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) ΔAPB≅ ΔCQD
(ii) AP = CQ
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔABC
(iv) AQ=CP
(v) APCQ is a parallelogram.

View Solution
