In Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
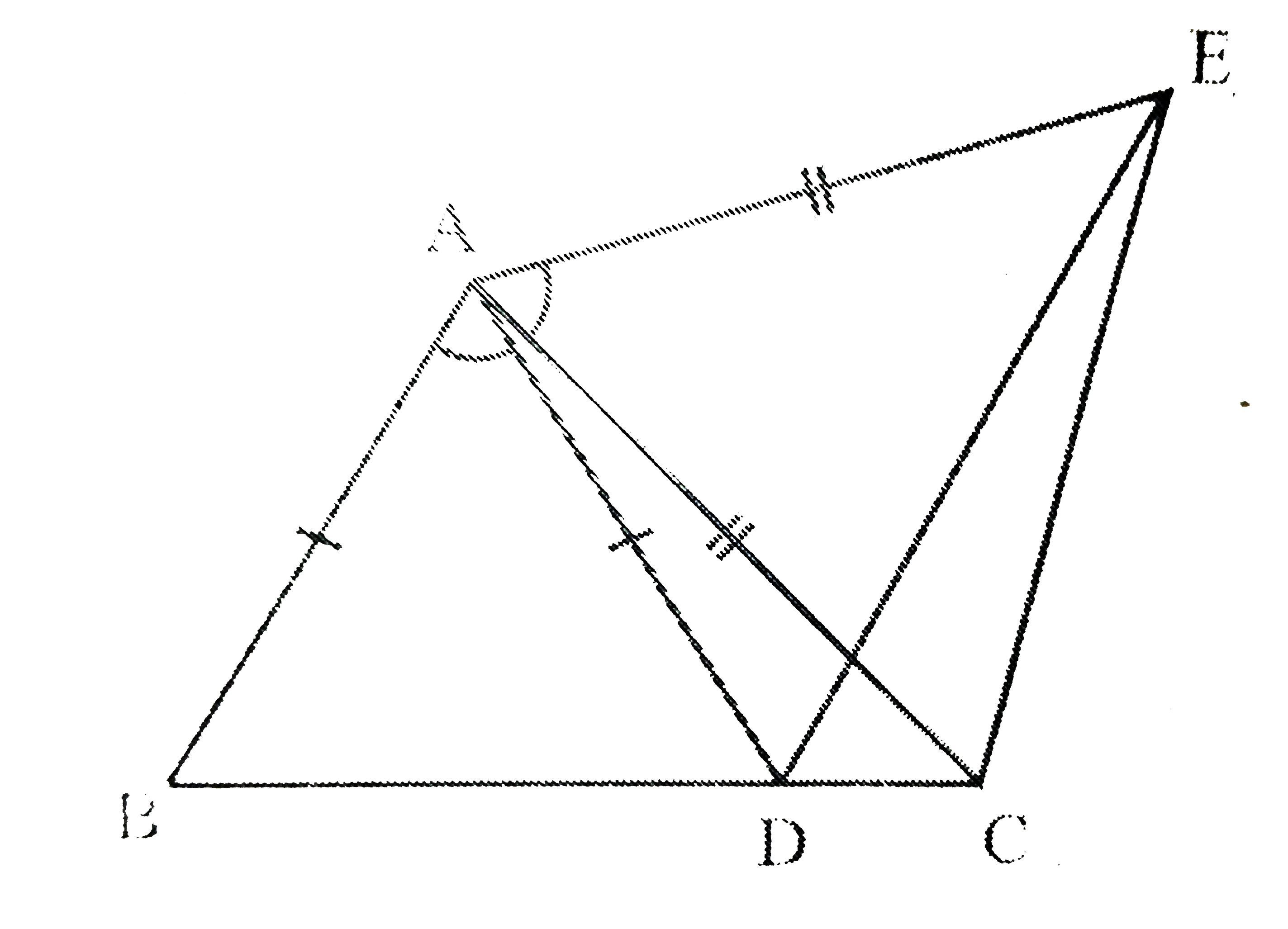
Given: AC=AE,AB=ADand∠BAD=∠EAC
To Prove: BC=DE
We can show two triangles BAC and DAE are congruent triangles by using the SAS congruency rule and then we can say corresponding parts of congruent triangles will be equal.
It is given that ∠BAD=∠EAC
Thus, by adding ∠DAC to both sides of this equation, we get
∠BAD+∠DAC=∠EAC+∠DAC (∠DAC is common)
∠BAC=∠DAE
In ΔBAC and ΔDAE,
AB=AD (Given)
∠BAC=∠DAE (Proven above)
AC=AE (Given)
∴ΔBAC≅ΔDAE (By SAS congruence rule)
∴BC=DE (By CPCT)
Topper's Solved these Questions
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.8
10 Videos
Similar Questions
In Fig. 71, if ABCD and CDEF, find ∠ACE
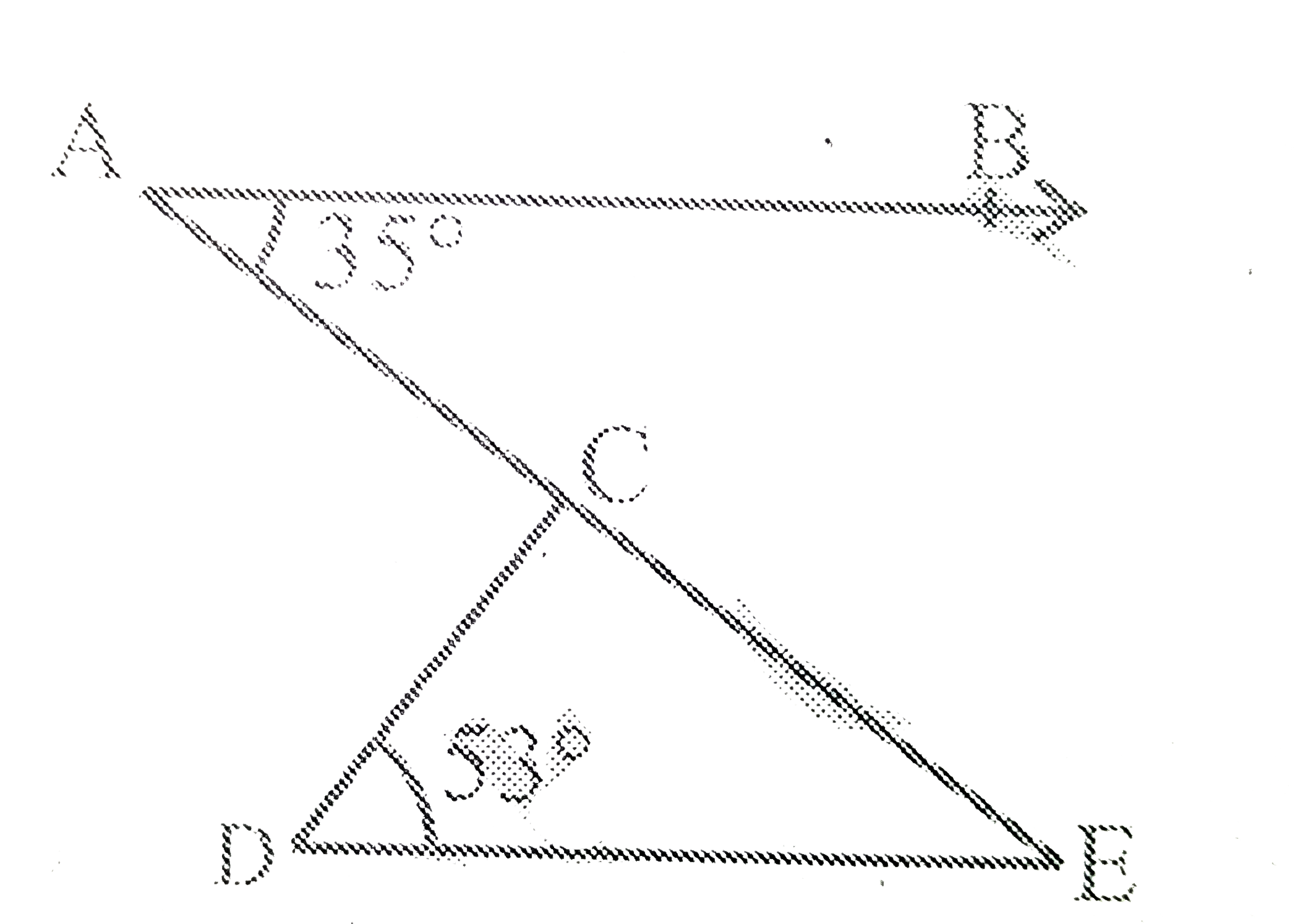
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
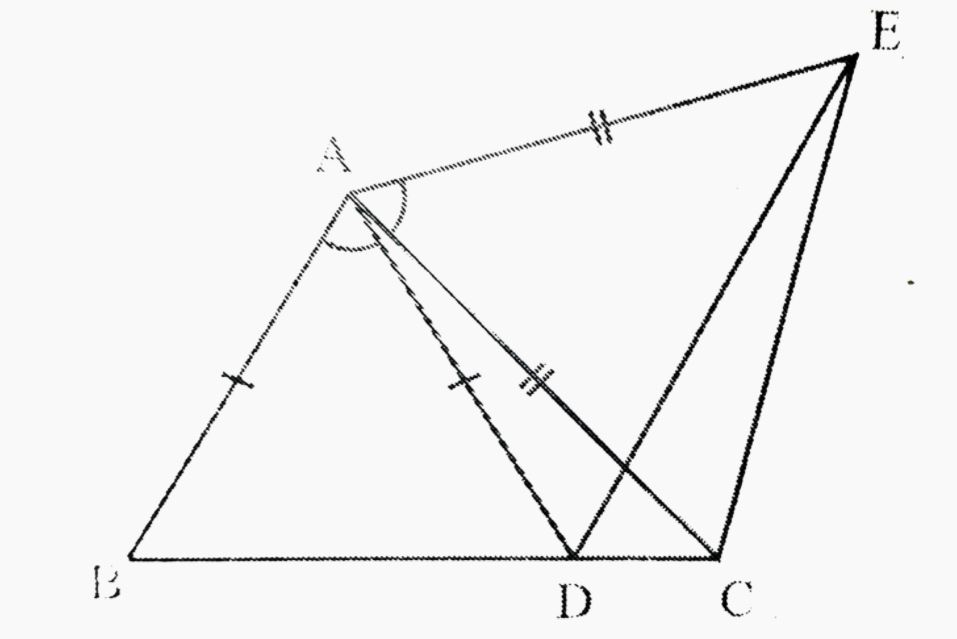
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
View SolutionIn Fig. 4.128, DEFG is a square and ∠BAC=90o . Prove that AGFDBG (ii) AGFEFC (FIGURE) (iii) DBGEFC (iv) DE2=BD×EC
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
View SolutionIn Fig. 15.63, ABCD is a trapezium with ABDC and ∠BCD=60o . If BFEC is a sector of a circle with centre C and AB=BC=7 cm and DE=4 cm , then find the area of the shaded region (Use π=227 and √3=1.732) .
View SolutionIn Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
View SolutionIn Fig. 4.101, AD and CE are two altitudes of ABC . Prove that AEF~CDF (ii) ABD~CBE (iii) AEF~ADB (iv) FDC~BEC (FIGURE)
View SolutionIn Figure, it is given that AB=BC and AD=EC. Prove that abe ≅CBD (ii) BD=BE
View Solution
