AB is a line segment and P is its midpoint. D and E are points on the same side of AD such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
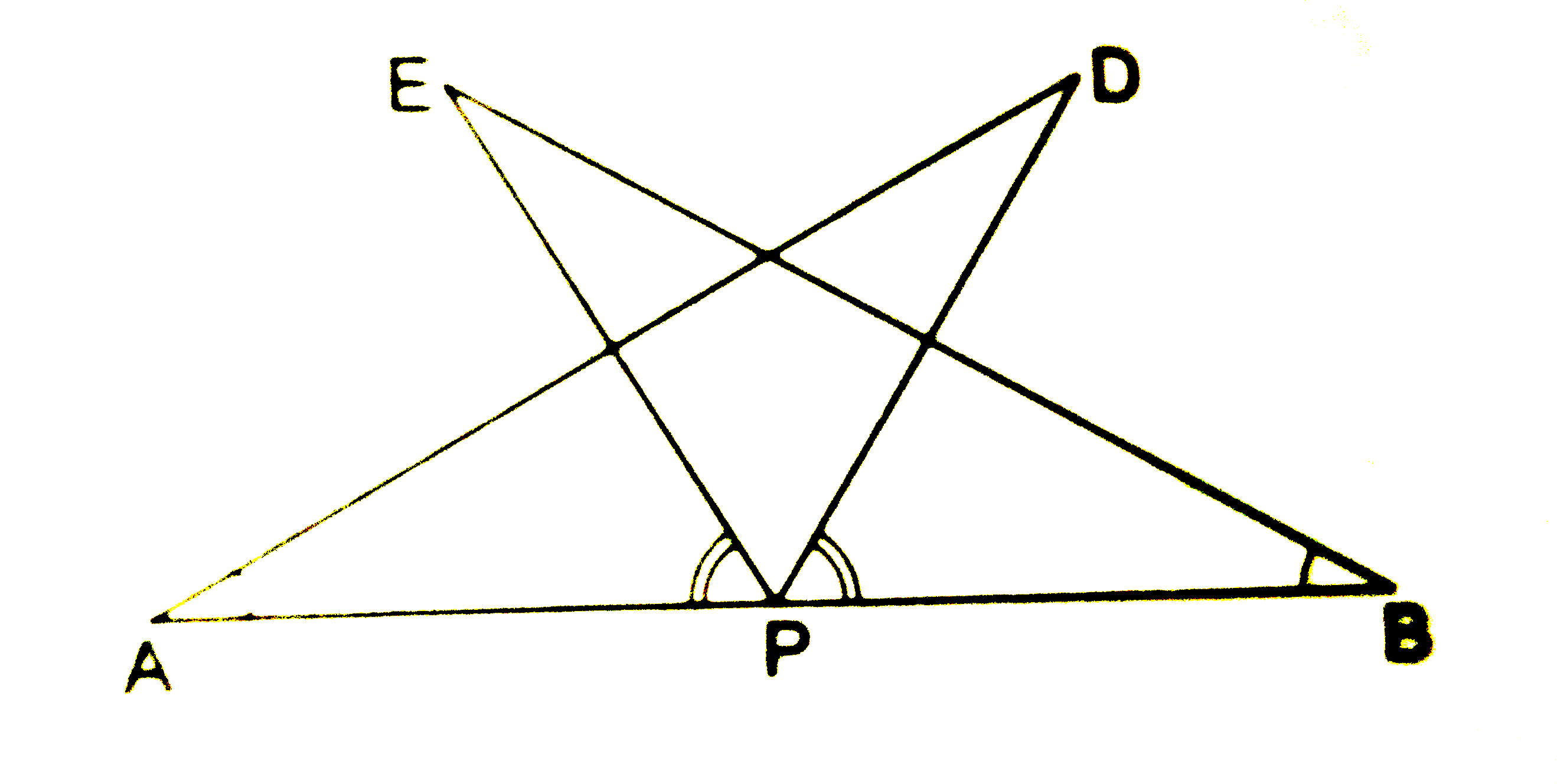
i) It is given that ∠EPA=∠DPB
∠EPA+∠DPE=∠DPB+∠DPE (∠DPE is common)
∴∠DPA=∠EPB
In ΔDAP and ΔEBP,
∠DAP=∠EBP (Given)
AP=BP (P is mid - point of AB)
∠DPA=∠EPB (Proven above)
∴ΔDAP≅ΔEBP(ASA congruence rule)
ii) Since, ΔDAP≅ΔEBP
∴ AD=BE (By CPCT)
Topper's Solved these Questions
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.8
10 Videos
Similar Questions
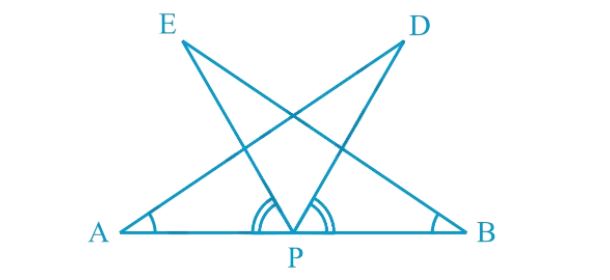
AB is a line segment D and P is its mid-point. D and E are points on the same side of AB such that ∠BAD=∠ABEand∠EPA=∠DPB (see figure). Show that

ΔDAP≅ΔEBP
View SolutionAB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD=∠ABEand∠EPA=∠DPB (see figure). Show that

AD=BE
View SolutionAB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
ΔDAP≡ΔEBP
View SolutionAB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
AD=BE
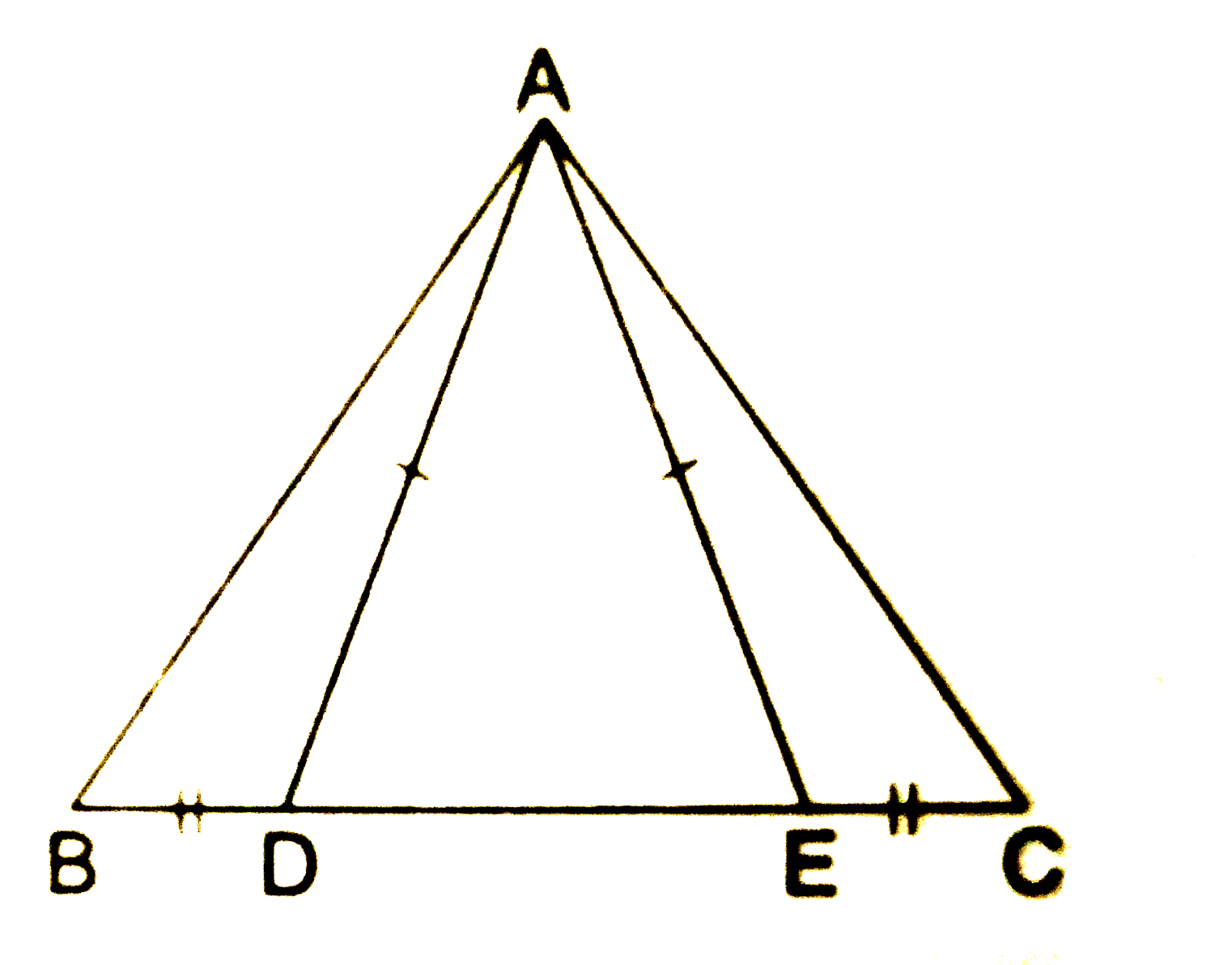
View SolutionIn the given figure, D and E are points on the side BC of a ΔABC such that BD = CE and AD = AE. Show that ΔABD≅ΔACE.
View SolutionD is a point on side BC of ΔABC such that AD=AC. Show that AB>AD.
View SolutionD and E are points on the sides AB and AC respectively such that AB=3.6 cm and AD=1.4 AC=7.2 and AE=1.8. Show that DE is parallel to BC
View SolutionD and E are points on the sides AB and AC respectively such that AB=3.6 cm and AD=1.4 AC=7.2 and AE=1.8. Show that DE is parallel to BC
View SolutionABC is a triangle in which AB=AC.DandE are points on the sides ABandAC respectively, such that AD=AE. Show that the points B<C<EandD are concyclie.
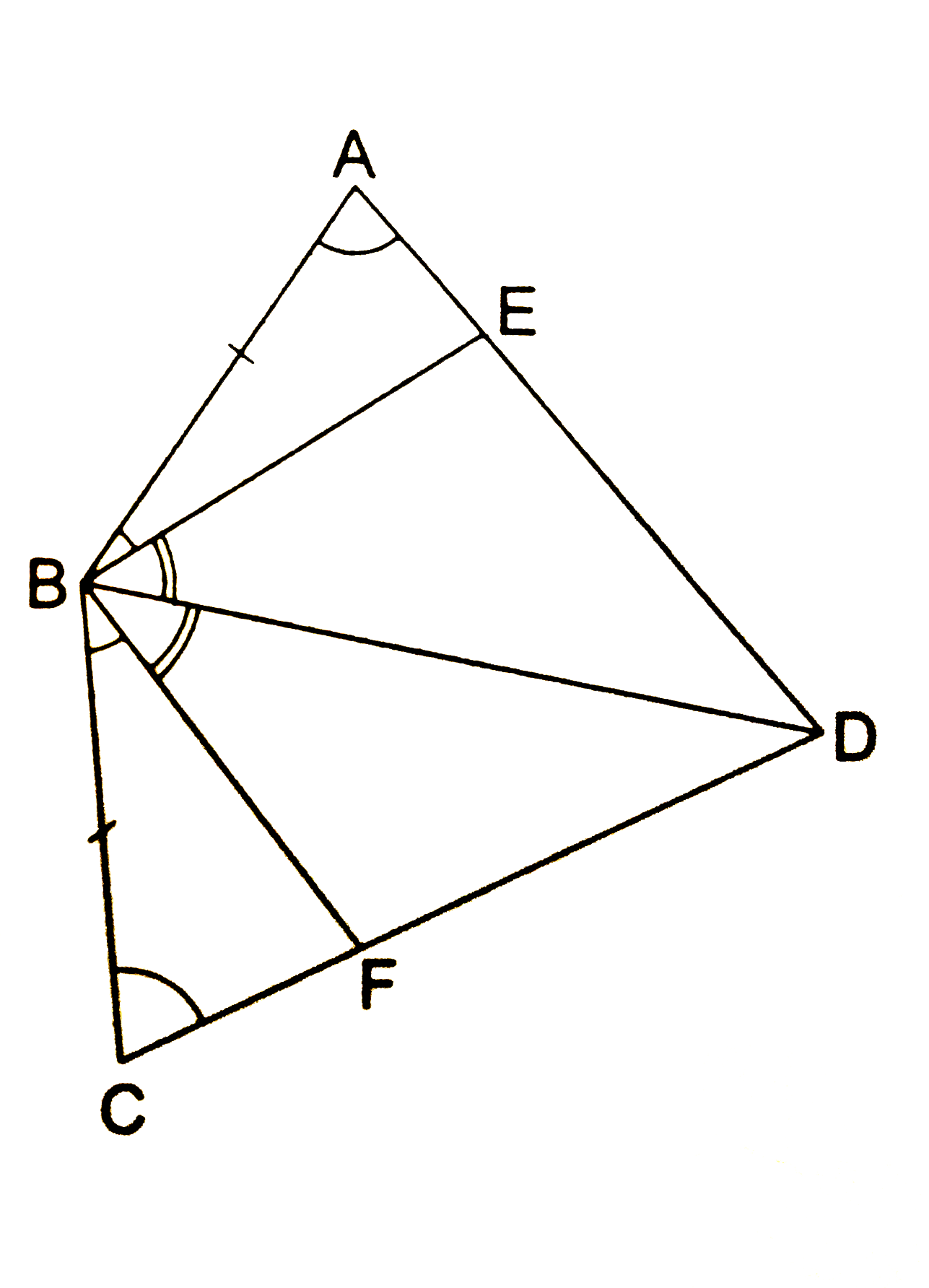
View SolutionIn the given figure, ABCD is a quadrilateral and E and F are points on AD and CD respectively such that AB = CB, ∠ABE=∠CBFand∠EBD=∠FBD. Prove that BE=BF.
View Solution
