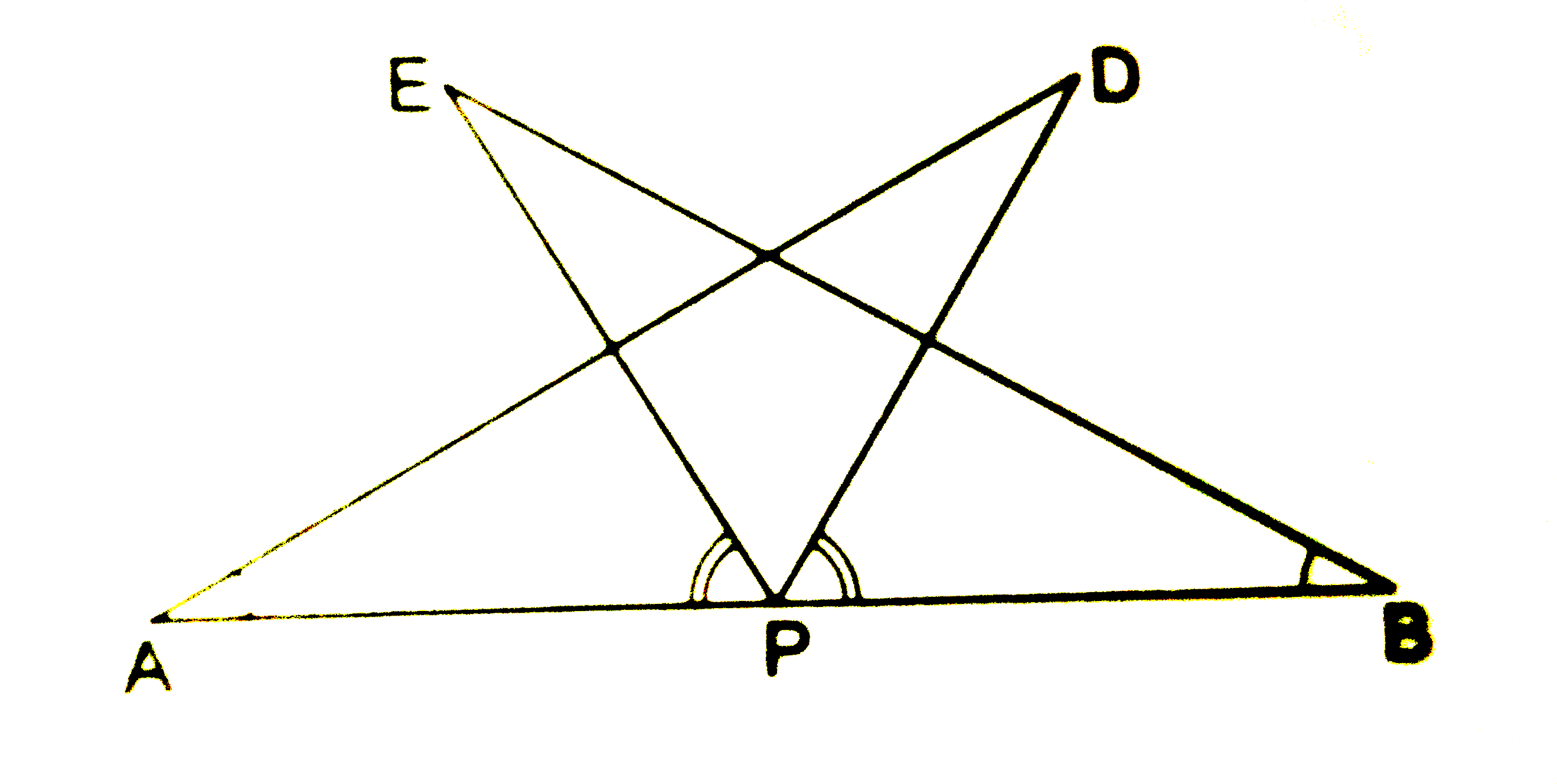
AB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
AD=BE
The correct Answer is:EF∣∣QR
Step by step video, text & image solution for AB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that angleBAD=angleABE and angleEPA=angleDPB. Prove that AD=BE by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONGRUENCE AND SIMILAR TRIANGLES BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5A
47 Videos
- CONGRUENCE AND SIMILAR TRIANGLES BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B
8 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
- ELEMENTARY TRIGONOMETRIC IDENTITIES BOOK - LUCENT PUBLICATIONCHAPTER - ELEMENTARY TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE 11B
37 Videos
Similar Questions
AB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
ΔDAP≡ΔEBP
View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AD such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
View Solution
Knowledge Check
A point C is called the midpoint of a line segment ¯¯¯¯¯¯AB if
AC is an intrerior points of ABBAC =CBCC is an interior point of AB such that ¯¯¯¯¯¯AC=¯¯¯¯¯¯CBDAC+CB=ABIf C and D are the points of internal and external division of line segment AB in the same ratio, then AC,AB, AD are in
AAPBGPCHPDAGP
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD=∠ABEand∠EPA=∠DPB (see figure). Show that

AD=BE
View SolutionAB is a line segment D and P is its mid-point. D and E are points on the same side of AB such that ∠BAD=∠ABEand∠EPA=∠DPB (see figure). Show that

ΔDAP≅ΔEBP
View SolutionIn the given figure, ABCD is a quadrilateral and E and F are points on AD and CD respectively such that AB = CB, ∠ABE=∠CBFand∠EBD=∠FBD. Prove that BE=BF.
View SolutionAB is a line segment. AX and BY are two equal line segments drawn on opposite sides of line AB such that AX∣∣BY. If AB and XY intersect each other at P,prove that APX≅BPY (ii) AB and XY bisect each other.
In the given figure, segment AXandBY are equa
View SolutionDandE are points on equal sides ABandAC of an isosceles triangle ABC such that AD=AE . Prove that B,C,D,E are concylic.
View SolutionD and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD=AE. Prove that B, C, D, E are concyclic.
View Solution
