An ideal gas with a known γ, completes a cycle consisting of two isotherms and two isobars. The isothermal processes are executed at temperatures T and T'(<T) and isobaric processes are completed at pressures P0 and eP0 [e = base of natural logarithm]. Find the efficiency of the cycle.
The correct Answer is:(T−T')(γ−1))(2γ−1)T−γT'
Step by step video, text & image solution for An ideal gas with a known gamma, completes a cycle consisting of two isotherms and two isobars. The isothermal processes are executed at temperatures T and T' (lt T) and isobaric processes are completed at pressures P_(0) and eP_(0) [e = base of natural logarithm]. Find the efficiency of the cycle. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 36videos
FIRST LAW OF THERMODYNAMICS
- BOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 36videos
FIRST LAW OF THERMODYNAMICS
- BOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 31videos
ELASTICITY
- BOOK - ARIHANTCHAPTER - FLUIDSEXERCISE - All Questions70videos
FLUIDS
Similar Questions
An adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.09:58View SolutionAn adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.05:28View SolutionA metal cylinder of length L and radius R is fixed rigidly to ground with its axis vertical. A twisting torque τ0 is applied along the circumference at the top of the cylinder. This causes an angular twist of θ0 (rad) in the top surface. Calculate the shear modulus of elasticity (η) of the material of the cylinder.
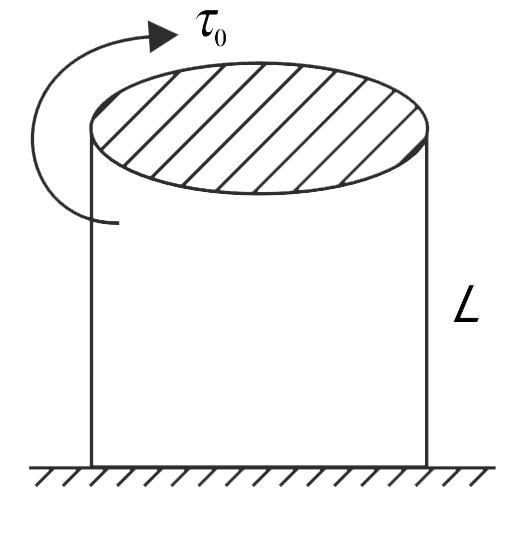 07:57View Solution
07:57View SolutionWe know that the atmospheric pressure on the surface of the earth is because of weight, of the air. The radius of the earth is 6400 km and atmospheric pressure on the sruface of earth is 1×105N/m2. Estimate the mass of the earth's atmosphere assuming that acceleration due to gravity remains constant at 10m/s2 over the entrie height of the atmospehre.
11:48View SolutionDraw the approximate plots of isochoric, isobaric, isothermal, and adiabatic processes for the case of an ideal gas, using the following variables : (a) p, T : (b) V , T .
09:14View SolutionFind the efficiency of a cycle consisting of two isobaric and two adiabatic lines, if the pressure changes n times within the cycle. The working substance is an ideal gas whose adiabatic exponent is equal to γ.
12:06View SolutionAn ideal gas whose adiabatic exponent equals γ goes through a cycle consisting of two isochoric and two isobaric lines. Find the efficiency of such a cycle, if the absolute temperature of the gas rises n times both in a isochoric heating and in the isobaric expansion.
05:36View SolutionAn ideal gas goes through a cycle consisting of (a) isochoric, adiabatic, and isothermal lines , (b) isobaric, adiabatic, and isothermal lines, with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the absolute temperature varies n-fold within the cycle.
06:31View SolutionAn ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies n−fold within the cycle.
View SolutionCalculate the efficiency of a cycle consisting of isothermal, isobaric, and isochoric line, if in the isothermal process the volume of the ideal gas with the adiabatic exponent γ.
(a) increased n−fold ,
(b) decreases n−fold.View SolutionFind the efficiency of a cycle consisting of two isochoric and two isothermal lines if the volume varies v−fold and the absolute temperature τ−fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
09:01View SolutionFind the efficiency of a cycle consisting of two isobaric and two isothermal lines if the pressure varies n−fold and the absolute temperature τ−fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
04:07View SolutionCalculate the efficiency of a cycle consisting of two isobaric and two adiabtic lines, if the pressure changes n=10 times within the cycle. The working substances is an ideal gas of adiabatic exponent gamma=1.5 .
View SolutionA gas (gamma=1.5) undergoes a cycle of adiabatic, isobaric and isochoric processes in an order. If the volume of the gas is doubled in the adiabatic process then the efficiency of the cycle is approximately,
04:19View SolutionThe efficiency of the cycle shown below in the figure ( consisting of one isobar , one adiabatic and one isotherm ( is 50 % the ratio ,x, between the highest and lowest temperature attained in this cycle obeys ( the working substance is an ideal gas )
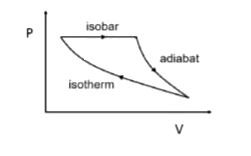 01:00:51View Solution
01:00:51View Solution

