Find the efficiency of a cycle consisting of two isobaric and two isothermal lines if the pressure varies n−fold and the absolute temperature τ−fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
Here Q1''=CpT0(τ−1),Q'1''=τRT01nn and
Q2''=CpT0(τ−1),Q2'''=RT01nn
in addition to we have
Q1=Q1'+Q1'' and
Q2'=Q2''+Q2'''
So η=1−Q'2Q1=1−Cp(τ−1)+R1nnCp(τ−1)+τR1nn
=1−τ−1+(1−1γ)1nnτ−1+(1−1γ)τ1nn
=1−τ−1+(1−1γ)1nnτ−1+(1−1γ)τ1nn=(τ−1)1nnτ1nn+γ(τ−1)γ−1.
 .
.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Liquids Capillary Effects
Explore 25 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Phase Transformations
Explore 35 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Kinetic Theory Of Gases
Explore 51 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
Find the efficiency of a cycle consisting of two isochoric and two isothermal lines if the volume varies v−fold and the absolute temperature τ−fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
View SolutionFind the efficiency of a cycle consisting of two isobaric and two adiabatic lines, if the pressure changes n times within the cycle. The working substance is an ideal gas whose adiabatic exponent is equal to γ.
View Solution
Knowledge Check
The efficiency of the cycle shown below in the figure ( consisting of one isobar , one adiabatic and one isotherm ( is 50 % the ratio ,x, between the highest and lowest temperature attained in this cycle obeys ( the working substance is an ideal gas )
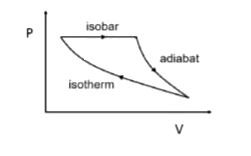 Ax=ex−1Bx2=ex−1Cx=ex2−1Dx2=ex2−1
Ax=ex−1Bx2=ex−1Cx=ex2−1Dx2=ex2−1An ideal gas goes through a cycle consisting of ischoric adiabatic and isothermal lines. The isothermal process is perform at minimum temperature. If the absolute temperature varies K times with tn the cycle then find out its effcincy.
 A1−lnKlB1+lnKlClnKlDllnK
A1−lnKlB1+lnKlClnKlDllnK
Calculate the efficiency of a cycle consisting of two isobaric and two adiabtic lines, if the pressure changes n=10 times within the cycle. The working substances is an ideal gas of adiabatic exponent γ=1.5.
View SolutionFind the efficiency of a cycle consisting of two isochoric and two adiabatic lines, if the volume of the ideal gas changes n=10 times within the cycle. The working substance is nitrogen.
View SolutionFind the efficiency of a cycle consisting of two isochoric and two adiabatic lines if the volume of the ideal gas changes n=10 times within the cycle. The working gas has γ=1.5.
View SolutionThe efficiency of the cycle shown below in the figure ( consisting of one isobar , one adiabatic and one isotherm ( is 50 % the ratio ,x, between the highest and lowest temperature attained in this cycle obeys ( the working substance is an ideal gas )

View SolutionAn ideal gas whose adiabatic exponent equals γ goes through a cycle consisting of two isochoric and two isobaric lines. Find the efficiency of such a cycle, if the absolute temperature of the gas rises n times both in a isochoric heating and in the isobaric expansion.
View SolutionCalculate the efficiency of a cycle consisting of isothermal, isobaric, and isochoric line, if in the isothermal process the volume of the ideal gas with the adiabatic exponent γ.
(a) increased n−fold ,
(b) decreases n−fold.
View Solution

