A heat engine is based on a gaseous cycle comprising of four processes viz. isothermal expansion at temperature (T1), isochoric cooling to temperature T2, isothermal compression (at T2) and isochoric heating back to temperature T1. The engine has been designed so as to completely use the heat rejected during isochoric cooling, in the isochoric heating process. Calculate the efficiency of this reversible cycle. Show the process on a PV graph.
The correct Answer is:η=T1−T2T1
Step by step video, text & image solution for A heat engine is based on a gaseous cycle comprising of four processes viz. isothermal expansion at temperature (T_(1)), isochoric cooling to temperature T_(2), isothermal compression (at T_(2)) and isochoric heating back to temperature T_(1). The engine has been designed so as to completely use the heat rejected during isochoric cooling, in the isochoric heating process. Calculate the efficiency of this reversible cycle. Show the process on a PV graph. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FIRST LAW OF THERMODYNAMICSBook:ARIHANTChapter:FIRST LAW OF THERMODYNAMICSExercise:Level 3
Explore 6 Videos
- FIRST LAW OF THERMODYNAMICSBook:ARIHANTChapter:FIRST LAW OF THERMODYNAMICSExercise:Level 3
Explore 6 Videos
- ELASTICITYBook:ARIHANTChapter:ELASTICITYExercise:Level 3
Explore 1 Video
- FLUIDSBook:ARIHANTChapter:FLUIDSExercise:All Questions
Explore 70 Videos
Similar Questions
An adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.
View SolutionAn adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.
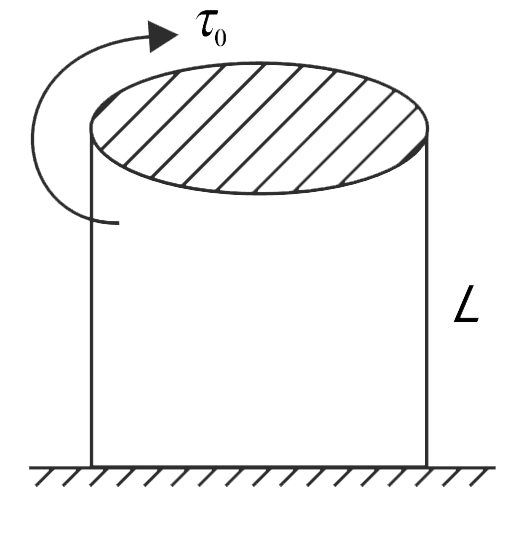
View SolutionA metal cylinder of length L and radius R is fixed rigidly to ground with its axis vertical. A twisting torque τ0 is applied along the circumference at the top of the cylinder. This causes an angular twist of θ0 (rad) in the top surface. Calculate the shear modulus of elasticity (η) of the material of the cylinder.
View SolutionWe know that the atmospheric pressure on the surface of the earth is because of weight, of the air. The radius of the earth is 6400 km and atmospheric pressure on the sruface of earth is 1×105N/m2. Estimate the mass of the earth's atmosphere assuming that acceleration due to gravity remains constant at 10m/s2 over the entrie height of the atmospehre.
View SolutionAn ideal heat engine working between temperature T_(1) and T_(2) has an efficiency eta , the new efficiency if both the source and sink temperature are doubled, will be
View SolutionWhat percentage T_(1) is of T_(2) for a 10% efficiency of a heat engine? T_(1) is the temperature of sink and T_(2) is the temperature of heat reservoir.
View SolutionIn the figure n mole of a monoatomic ideal gas undergo the process ABC as shown in the P-V diagram. The process AB is isothermal and BC is isochoric. The temperature of the gas at A is T_(0) total heat given to the gas during the process ABC is measured to be Q. Heat absorbed by the gas in the process BC
View SolutionIn an isochoric process if T1=27∘C and T2=127∘C then P1/P2 will be equal to
View SolutionThe efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . eta = (W)/(Q_(1)) = (Q_(1) - Q_(2))/(Q_(1)) Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression. For carnot cycle (Q_(1))/(T_(1)) = (Q_(2))/(T_(2)) . Thus eta = (Q_(1) - Q_(2))/(Q_(1)) = (T_(1) - T_(2))/(T_(1)) According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs". A carnot engine whose low temperature reservoir is at 7^(@)C has an efficiency of 50% . It is desired to increase the efficiency to 70% . By how many degrees should the temperature of the high temperature reservoir be increased?
View SolutionThe efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . η=WQ1=Q1−Q2Q1 Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression.
_E01_238_Q01.png)
For carnot cycle Q1T1=Q2T2. Thus η=Q1−Q2Q1=T1−T2T1 According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs"._E01_238_Q02.png)
Efficiency of a carnot's cycle change from 16 to 13 when source temperature is raised by 100K. The temperature of the sink is-
View SolutionA reversible heat engine A(based on carnot cycle ) absorbs heat from a reservoir at 1000 K and rejects heat to a reservoir at T2 . A second reserviour at T2 and rejects energy to a reservoir at 360 K . If the efficiencies of engines A and B are the same then the temperature T2is .
View SolutionThe efficiency of carnot's heat engine is 0.5 when the temperature of the source is T1 and that of sink is T2 .The efficiency of another carnot's heat engine is also 0.5.the temperature of source and sink of the second engine are respectively
View SolutionTwo curves are given at temperatures T_(1) and T_(2) in an isothermal process, then-
View SolutionThe efficiency of Carnot's heat engine is 0.5 when the temperature of the source is T_(1) and that of sink is T_(2) . The efficiency of another Carnot's heat engine is also 0.5 Then temperature of source and sink of the second engine are respectively
View SolutionIsochoric Process|Isothermal Process
View Solution

