A long cylindrical conductor of radius a has two cylindrical cavities of diameter a through its entire length as shown in cross-section in figure. A current I is directed out of the page and is uniform throughout the cross-section of the conductor. Find the magnitude and direction of the magnetic field in terms of μ0,I,r and a.
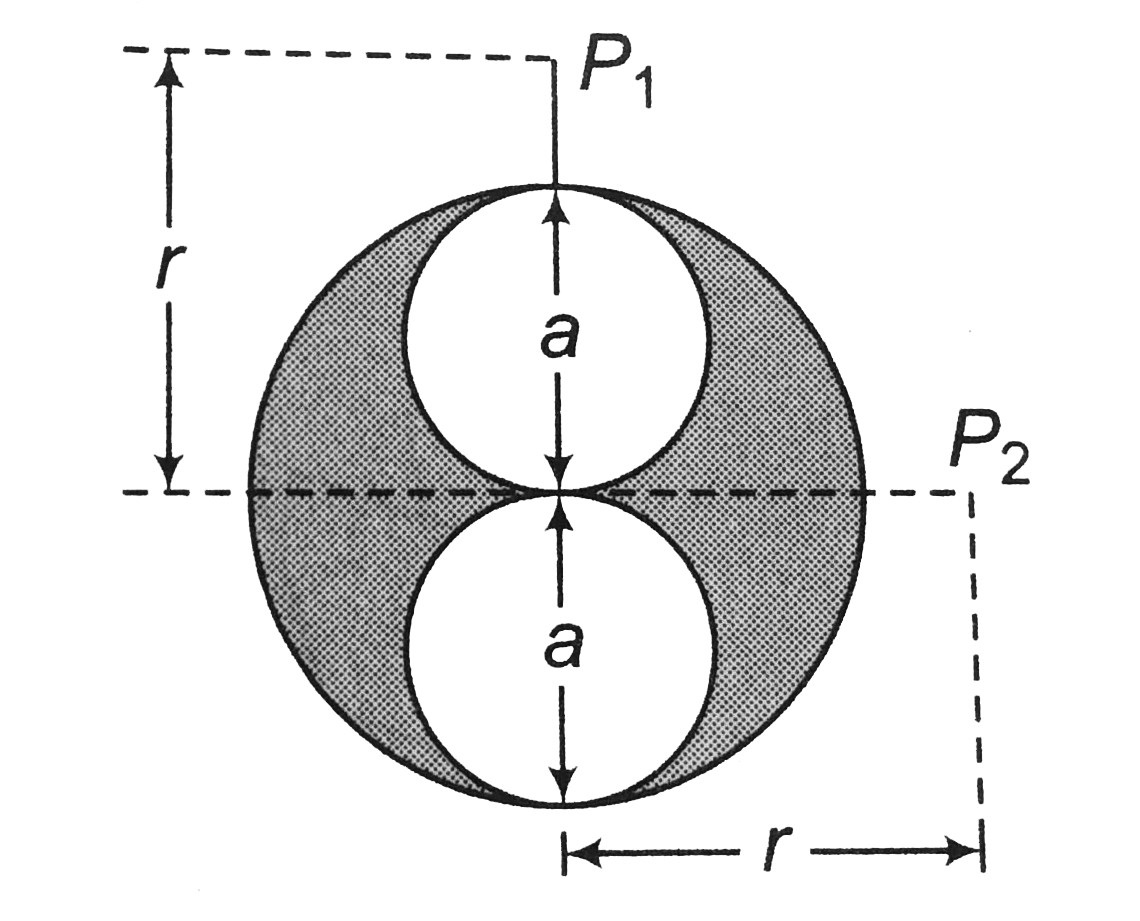
(a) at point P1 and (b) at point P2
(a)μ0I4r(2r2−a24r2−a2) to the left
(b)μ0Iπr(2r2+a24r2+a2) towards the top of the page

Current density J=1πa2−2π(a2)2=2Iπa2
Let us consider both the cavities are carrying equal and opposite currents with current density J.
Let B1,B2 and B3 be magnetic fields due to complete cylinder, upper and lower cavity respectively.
(a) At point P1
→B1=−μ04π.2I1rˆi=−μ04π.2J×πa2rˆi=−μ0Iπr
→B2=μ04π.2I2aˆi=μ04π.2J×π(a2)2r−a2ˆi
=−μ0I4π(r−a2)ˆi
→B3=μ04π.2I3r+a2ˆi=μ04π(r+a2)ˆi
→B=→B1+→B2+→B3
=μ0I4π[−4r+1r−a2+1r+a2]ˆi
→B=μ0I4πr[2r2−a24r2−a2]ˆi
∴(→B)=μ0I4πr[2r2−a24r2−a2], towards left.
(b) At point P2

→B1=μ04π.2I1rˆj=μ0Iπrˆj
→B2=μ04π.2I2√r2+a24[sinθˆi−cosθˆj]
=−μ0I2π√4r2+a2[sinθˆi+cosθˆj]
→B3=μ04π.2I3√r2+a24[sinθˆi−cosθˆj]
=μ0I2π√4r2+a2[sinθˆi−cosθˆj]
→B=→B1+→B2+→B3=μ0I2π[2r−2cosθ√4r2+a2]ˆj
but cosθ=r√r2+a24=2r√4r2+a2
∴→B=μ0I2π[2r−4r4r2+a2]ˆj
=μ0I4πr[2r2+a24r2+a2]ˆj
(→B)=μ0I4πr[2r2+a24r2+a2], upwards.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level =I (H.W)
Explore 42 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level -II (H.W)
Explore 37 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-V (SINGLE ANSWER QUESTION)
Explore 85 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
A long cylindrical conductor of radius R has two cylindrical cavities of diameter R through its entire length, as shown in the figure. There is a current I through the conductor distributed uniformly in its entire cross section (apart from the cavity region). Find magnetic field at point P at a distance r=2R from the axis of the conductor (see figure).

View SolutionThere are two parallel current carrying wires X and Y as shown in figure. Find the magnitude and direction of the magnetic field at points, P, Q and R.
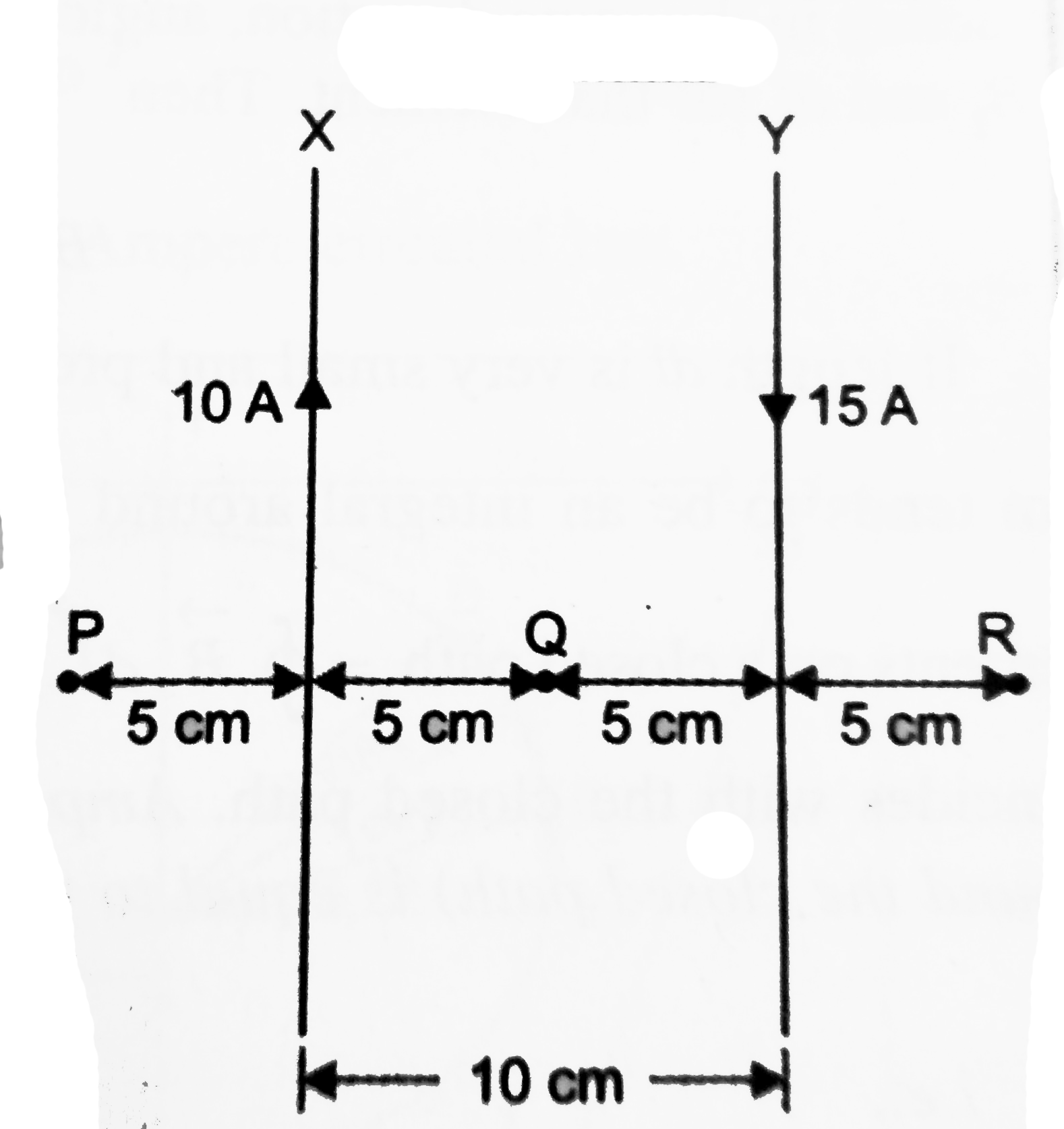
View Solution
Knowledge Check
A long cylindrical conductor of radius R having a cylindrical cavity of radius R/2 through out its length is lying with its axis parallel to x-axis. The distance between the axes of the cylinder and the cavity length in the positive x direction. The across sectional view of the cylinder is shown in the figure

The magnetic induction at point on the cavity isAμ0I3πR(−ˆl)Bμ0i3πR(ˆk)Cμ0i6πR(ˆj)Dμ0I6πR(−ˆj)
Two infinite plates shown in cross-section in figure carry λ amperes of current out of thepage per unit width of plate. Find the magnetic field at points P and Q.

View SolutionIn a long insulating cylinder of radius R a cylindrical tunnel of radius a located at a distance b from the axis of the cylinder as shown in the figure. R R b - The solid part of the cylinder has a uniform volume charge density P. Find the magnitude and direction of the electric field inside the tunnel.
View SolutionIn the figure are shown two long parallel current carrying wires I and II. Find the magnitudes and directions of the magnetic field induction at the point P, Q and R in the plane of paper.

View SolutionCalculate the magnitude of the magnetic field at point P as shown in Fig, in terms of R,I1andI2.

View SolutionFigure shows a cross-section of a long ribbon of width ω that is carrying a uniformly distributed total current i into the page. Calculate the magnitude and direction of the magnetic field B at a point P in the plane of the ribbon at a distance d from its edge.

View SolutionAn electric current of I ampere is flowing in a long conductor CG as shown in figure. Find the magnitude and direction of magnetic induction at the centre O of circular part.
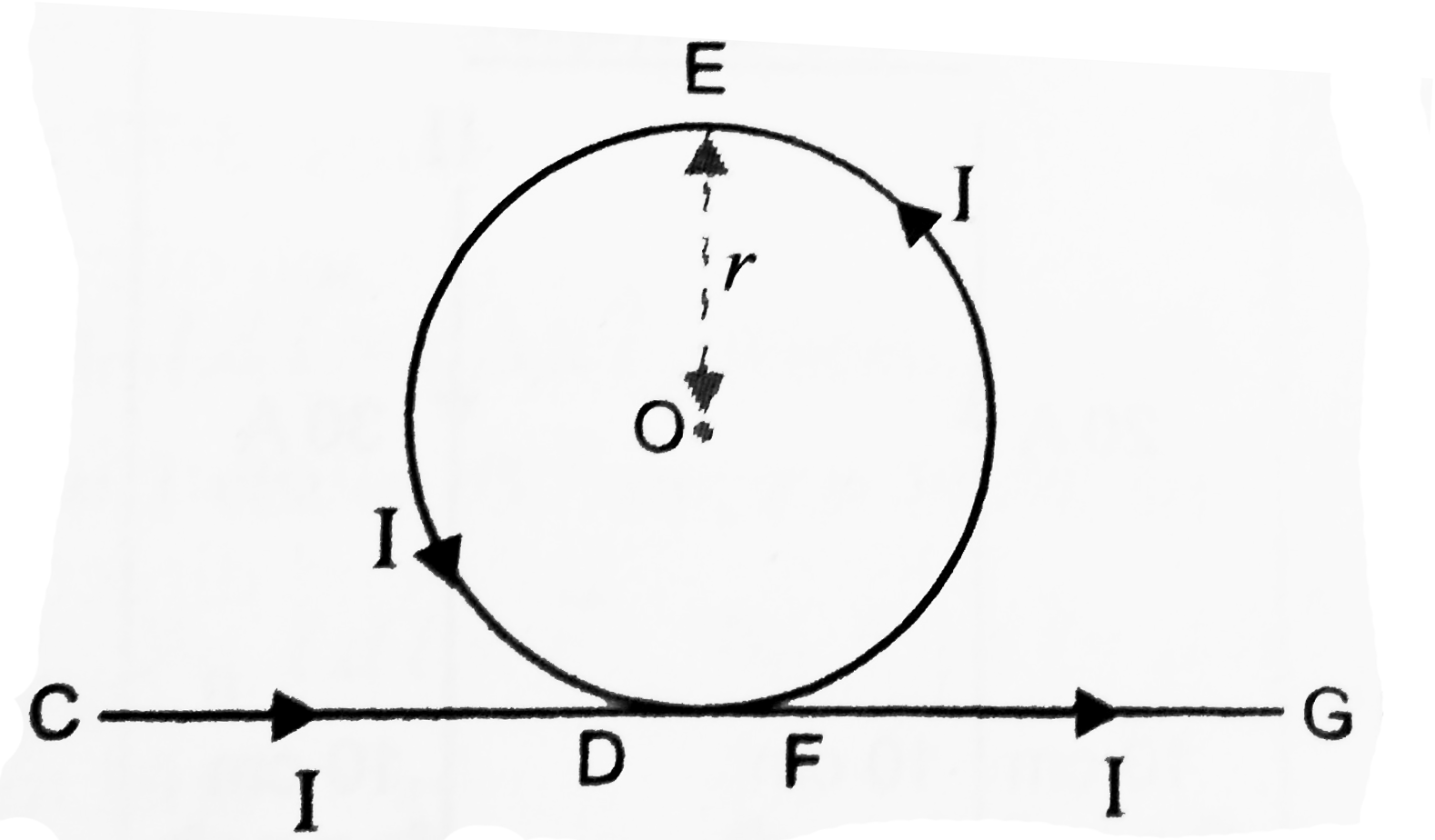
View SolutionA current I flows in a long straight wire whose cross section is in the shape of a thin quarter ring of radius R. Find the induction of the magnetic field (B) at point O on the axis.

View Solution

