A current of 10A flows around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists oif eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
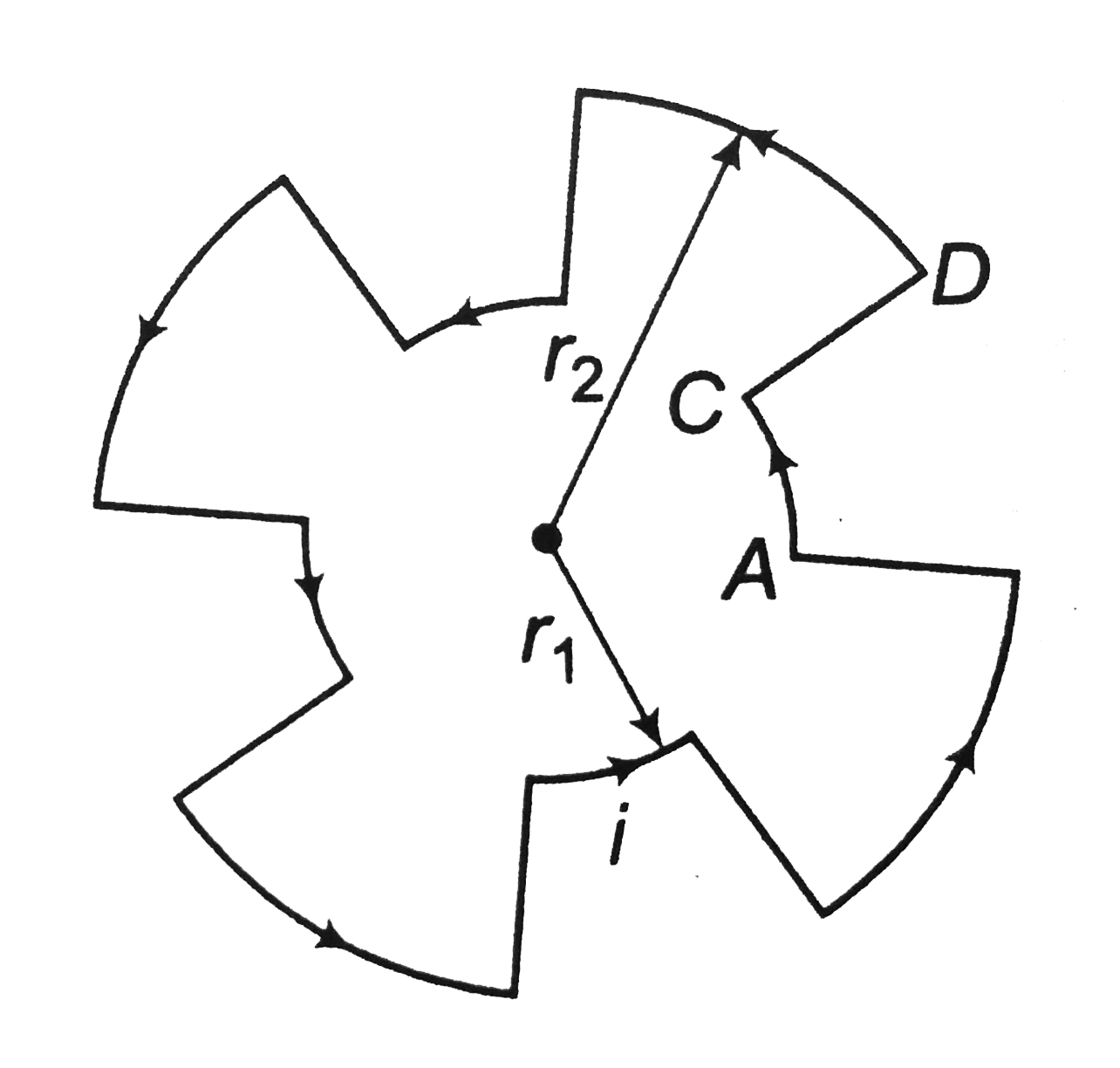
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carryin as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centre due to the current in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
For finding the magnetic field produced by this circuit at the centre we can consider. It to contain of two semicircles of radius r1=0.08m and r2=0.12m . Since current is flowing in the same direction the magnetic field created by circular arcs will be in the same direction and hence added
∴B1=μ0i4r1 and B2=μ0i4r2
∴B=μ0i4[1r1+1r2]( Direction outwards )
∴B=(6.54×10−5)T ( Right hand thumb rule )
(b) Force acting on a current carrying conductor plaed in a magnetic field is given by
F=I(l×B)IlBsinθ
In this case θ0∴F=0
(ii) On arc AC due to current at the centre ∣∣→B∣∣ at AC will be B=μ0I2πr1 . The direction of this magnetic field on any small segment of AC will be tangential ∴θ=180∘∴F=0
(iii) On segment CD
Force on a small segment dx distant r from O
dF=IdxB=10×dx×μ0I2πx
∴=5μ0Iπdxx On integrating
∴F=5μ0Iπ∫r2r1drr∴F=5μ0Iπ[loger]r2r1
∴F=5μ0Iπloge.r2r15μ0×10πloge(0.120.08)=8.1×10−6N
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level =I (H.W)
Explore 42 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level -II (H.W)
Explore 37 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-V (SINGLE ANSWER QUESTION)
Explore 85 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
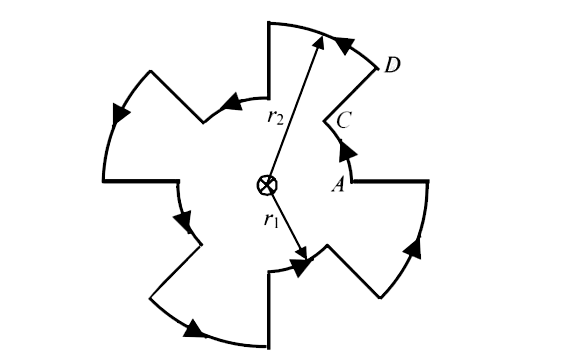
A current of 10A flows around a closed path in a circuit which is int eh horizontal plne as shown in the figure. The circuit consists oif eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.

a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carryin as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centredue to the curren in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
View SolutionA current of 10A flows around a closed path in a circuit which is in horizontal plane as shown in the figure . The circuit consists of eight alternating arcs of radiir1=0.08mandr1=0.12m.Eacharc⊂tendsthesameathecenter.<br>(a)F∈dthemag≠tixcfield∏ucedbythis∘uitatthecenter.<br>(b)An∈f∈itelylongstraightwirecarry∈gacurrentof10 Aispassingthroughthecenteroftheabove∘uitverticallywiththedirectionofthecurrentbe∈g∫othepla≠ofthe∘uit.Wˆistheforceact∈gonthearcACandthestraightsegment CD due to the current at the center?
View Solution
Knowledge Check
A current I flows around a closed path in the horizontal plane of circle as shown in the figure The path consists of eight arcs with alternating radii r and 2r . Each segment of arc subtends equal angle at the common centre P The magnetic field produced by current path at point P is
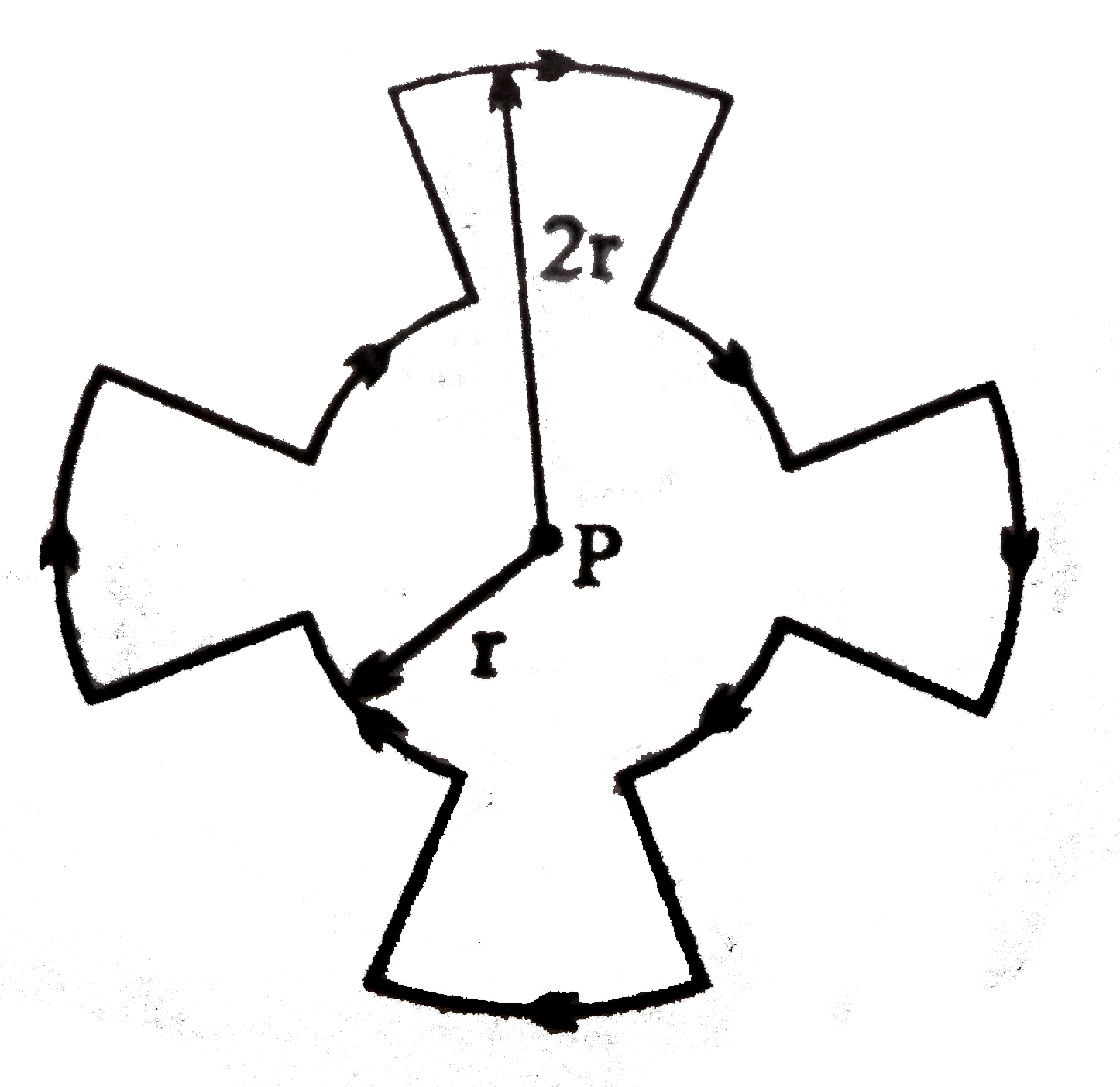 .A38μ0Ir , perpendicular to the plane of the paper and directed inward .B38μ0Ir , perpendicular to the plane of the paper and directed outward .C38μ0Ir , perpendicular to the plane of the paper and directed inward .D38μ0Ir , perpendicular to the plane of the paper and directed outward .
.A38μ0Ir , perpendicular to the plane of the paper and directed inward .B38μ0Ir , perpendicular to the plane of the paper and directed outward .C38μ0Ir , perpendicular to the plane of the paper and directed inward .D38μ0Ir , perpendicular to the plane of the paper and directed outward .In the circuit shown in figure current in the circuit is
 A1.27AB2.23AC4.26AD4 A
A1.27AB2.23AC4.26AD4 AThe magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
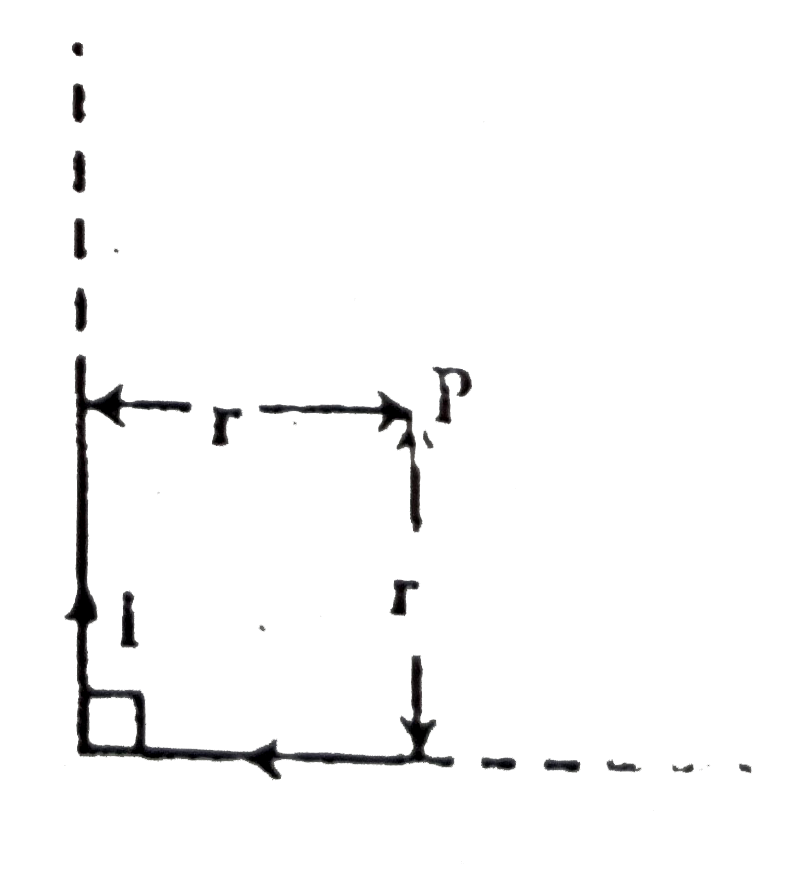 Aμ0Bμ0i/2√2rC(μ0i/√2πr)Dμ0i4πr[2+√2]
Aμ0Bμ0i/2√2rC(μ0i/√2πr)Dμ0i4πr[2+√2]
Switch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionFind the current ( in ampere) through wire XY of the circuit shown in figure.
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.

View SolutionAn L-R circuit has a cell of e.m.f. E , which is switched on at time t = 0. The current in the circuit after a long time will be
View Solution

