The inductor in a oscillation has a maximum potential difference of and maximum energy of . Find the value of capacitor in in circuit.
The correct Answer is:5
To find the value of the capacitor in an L-C circuit given the maximum potential difference and maximum energy, we can follow these steps:
1. Identify Given Values:
- Maximum potential difference (V) = 16 V
- Maximum energy (U) = 640 µJ = 640 × 10^(-6) J
2. Use the Formula for Energy in a Capacitor:
The energy stored in a capacitor is given by the formula:
U=12CV2
where C is the capacitance in farads and V is the potential difference.
3. Rearrange the Formula to Solve for Capacitance (C):
Rearranging the formula gives:
C=2UV2
4. Substitute the Known Values:
Substitute U=640×10−6 J and V=16 V into the equation:
C=2×640×10−6162
5. Calculate the Denominator:
Calculate 162:
162=256
6. Calculate the Capacitance:
Now substitute back into the equation:
C=1280×10−6256
C=5×10−6 F
7. Convert to Microfarads:
Since 1 \text{ F} = 10^6 \text{ µF} :
C=5 µF
Final Answer:
The value of the capacitor in the L-C circuit is 5 µF.
- Maximum potential difference (V) = 16 V
- Maximum energy (U) = 640 µJ = 640 × 10^(-6) J
The energy stored in a capacitor is given by the formula:
U=12CV2
where C is the capacitance in farads and V is the potential difference.
Rearranging the formula gives:
C=2UV2
Substitute U=640×10−6 J and V=16 V into the equation:
C=2×640×10−6162
Calculate 162:
162=256
Now substitute back into the equation:
C=1280×10−6256
C=5×10−6 F
Since 1 \text{ F} = 10^6 \text{ µF} :
C=5 µF
The value of the capacitor in the L-C circuit is 5 µF.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level =I (H.W)
Explore 42 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level -II (H.W)
Explore 37 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-V (SINGLE ANSWER QUESTION)
Explore 85 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
A capacitor in an LC oscillator has a maximum potential difference of 17 V and a maximum energy of 160 μJ. When the capacitor has a potential difference of 5 V and an energy of 10 μJ, what are (a) the emf across the inductor and (b) the energy stored in the magnetic field?
View SolutionA 1.5 mH inductor in LC circuit stores a maximum energy of 17μ J. What is the peak current ?
View Solution
Knowledge Check
A capacitor in an LC oscillator has a maximum potential difference of 17V and a maximum energy of 160μJ.When the capacitor has a potential difference of 5V and an energy of 10μJ, what is the energy stored in the magnetic field?
A10μJB150μJC160μJD170μJA capacitor in an LC oscillation has a maximum potential difference of 1.5 and a maximum energy 360μJ. At a certain instant t=t0, the potential difference across the capacitor is V volt?
AThe value of capacitance isBThe value of capacitance isCThe value of V is 5 voltDThe value of V is 10voltA capacitor in LC oscillatory circuit has a maximum potential of V volts and maximum energy E. When the capacitor has a potential V1 volts and energy E1 joules, what is the emf across the inductor and energy stered in the magnetic field
AV−V1,E−E1BV−V1,E1CV1,E1DV1,E−E1
It is desired to set up an undriven L-C circuit in which the capacitor is originally charged to potential difference of 100.0 V . The maximum current is to be 1.0 A and the oscillation frequency is to be 1000 Hz . What are the required values of L and C ?
View SolutionInitially, the capacitor is charged to a potential of 5V and then connected to position 1 with the shown polarity for 1s. After 1s it is connected across the inductor at position 2
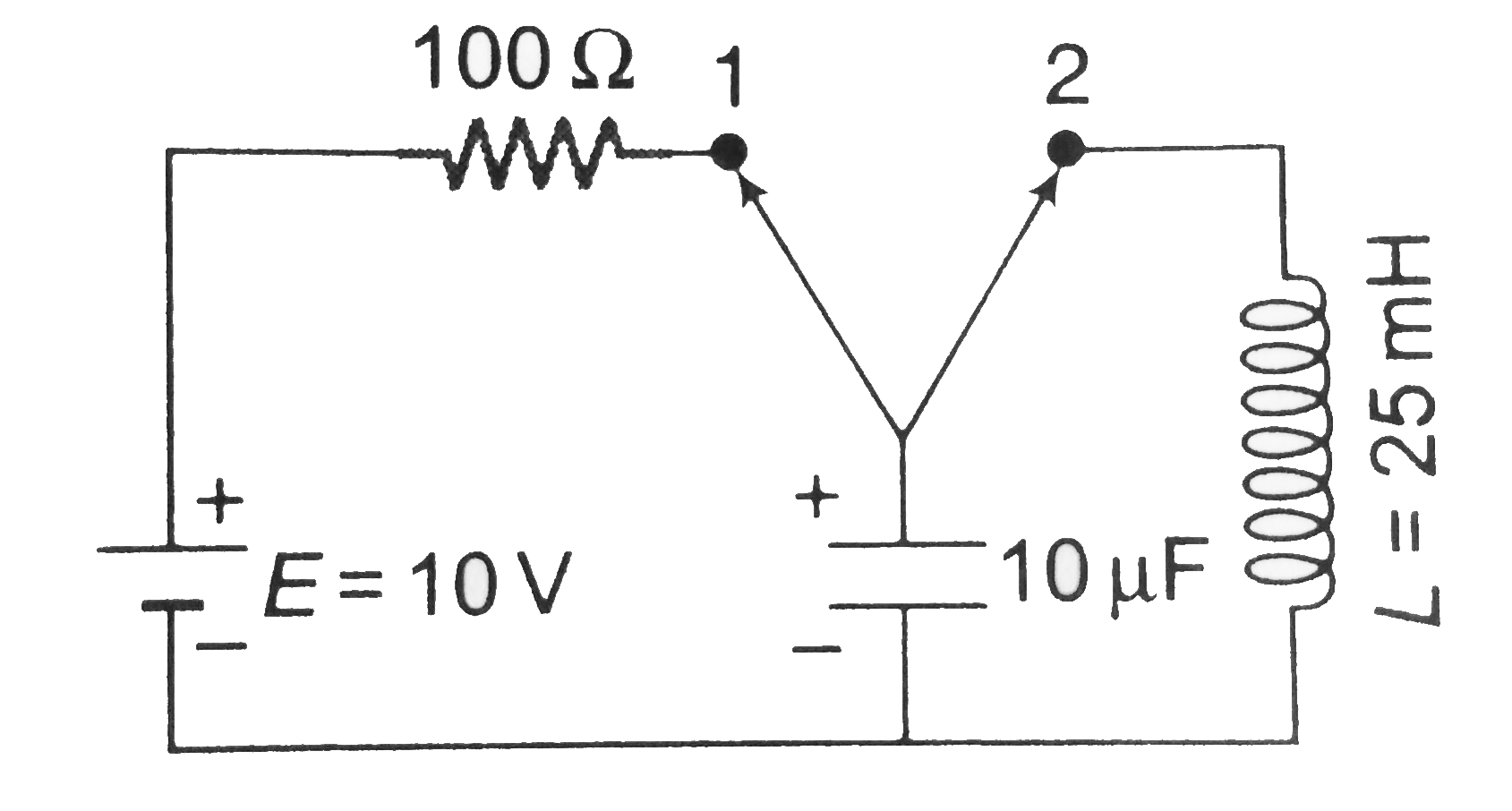
(a) Find the potential across the capacitor after 1s of its connection to position 1.
(b) Find the maximum current flowing in the L−C circuit when capacitor is connected across the inductor. Also, find the frequency of LC oscillations.
View SolutionA 1.5 mH inductor in an LC circuit stores a maximum energy of 30μJ. What is the maximum current in the circuit ?
View SolutionIn the given circuit , the potential difference between A and B is 18 V and charge on 2 μF capacitor is 24 μ C . The value of C is

View SolutionA capacitor of capacitance 25μF is charged to 300V. It is then connected across a 10mH inductor. The resistance in the circuit is negligible.
a. Find the frequency of oscillation of the circuit.
b. Find the potential difference across capacitor and magnitude of circuit current 1.2ms after the inductor and capacitor are connected.
c. Find the magnetic energy and electric energy at t=0 and t=1.2ms.
View Solution