A circular loop of radius R is bent along a diameter and given a shapes as shown in the figure. One of the semicircles (KNM) lies in the x−z plane with their centres and the other one (KLM) in the y−z plane with their centres at the origin. current I is flowing through each of the semi circles as shown in figure.
(a) A particle of charge q is released at the origin with a velocity →v=−v0ˆi. Find the instantaneous force →F on the particle . Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied , determine the force →F1and→F2 on the semicircles KLMandKNM due to the field and the net force →F on the loop.
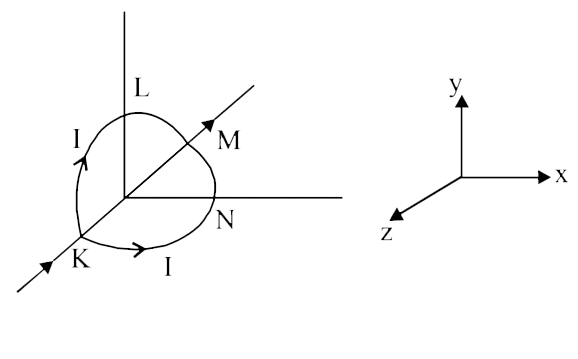
(a) Magnetic filed (→B) at the origin = magnetic field due to other semicirle KLM+ Magnetic field due to other semicircle KNM.
Therefore,
→B=−μ0I4R(−ˆi)+μ0I4R⇒→B=−μ04Rˆi+μ0I4R(−ˆi+ˆj)
∣∣→B due to a circular current carrying loop is
μ0I2R For semicircle it is half ∣
Therefore magnetic force acting on the particle
→F=q{(−v0ˆi)×(−ˆi+ˆj)×μ0I4R}=−μ0qv0I4Rˆk
(B)→FKLM=→FKNM=→FKM
and →FKLM=BI(2R)ˆi=2BIRˆi
Total force on the loop =4BIRˆi
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level =I (H.W)
Explore 42 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level -II (H.W)
Explore 37 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-V (SINGLE ANSWER QUESTION)
Explore 85 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
A circular loop of radius R is bent along a diameter and given a shape as shown in figure. One of 30,A the se micircles (KNM) lies in the xz-plane and the other one (KLM) in the yz-plane with their centres at origin. Current I is flowing through each of the semicircles as shown in figure.
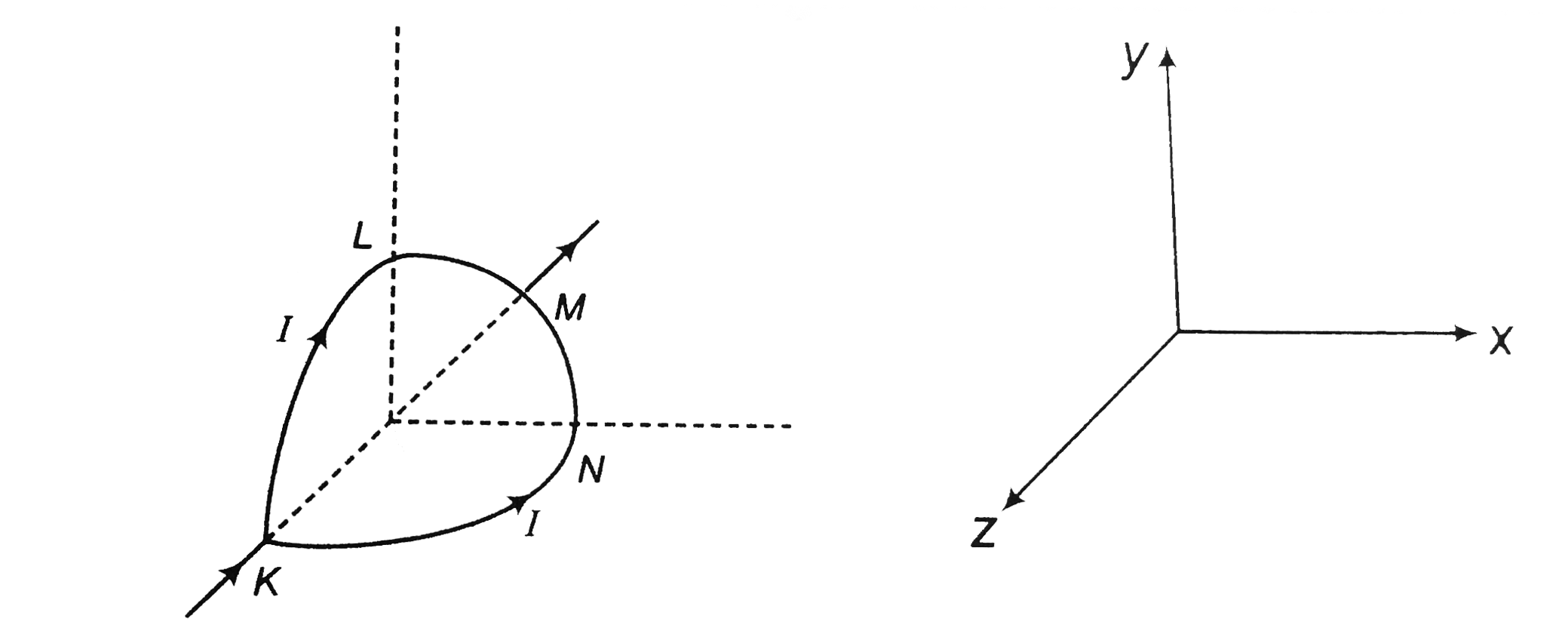
(a) A particle of charge q is released at the origin with a velocity v=−v0ˆi. Find the instantaneous force F on the particle. Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied, determine the force F1 and F2 on the semicircles KLM and KNM due to the field and the net force F on the loop.
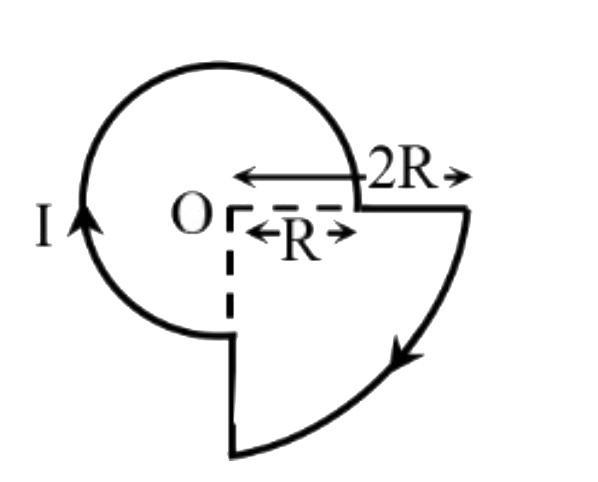
View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
View Solution
Knowledge Check
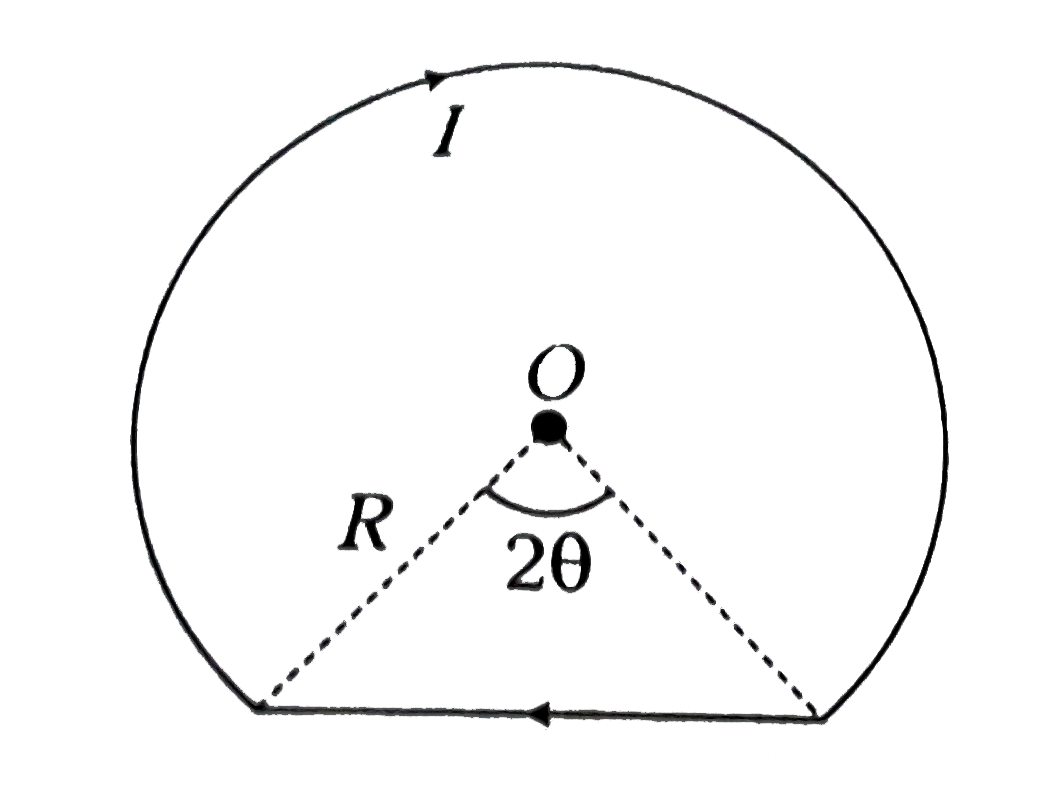
A current I flows through a closed loop as shown in figure. The magnetic field induction at the centre 0 is
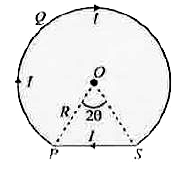 Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)
Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)A current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
 Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)
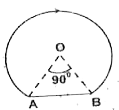
Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)A current I flows through a closed loop as shown in figure .The magnetic field at the centre O is
 Aμ0I2πR(π−θ+tanθ)Bμ0I2πR(π−θ+sinθ)Cμ0I2πR(θ+sinθ)DNone of these
Aμ0I2πR(π−θ+tanθ)Bμ0I2πR(π−θ+sinθ)Cμ0I2πR(θ+sinθ)DNone of these
As current I flowing through the loop as shown in figure. The magnetic field at the centre O is
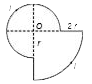
View SolutionA circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

View SolutionA circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
View Solution

