Two long concentric cylindrical conductors of radii a and b (b<a) are maintained at a potential difference V and carry equal opposite current I. Show that an electron with a particular velocity u parallel to the axis may travel undeviated in the evacuated region between the conductors.
The electric field E in the region between the conductors varies with the diameter r from the axis as E=λ2πε0r
Where λ is the charge per unit length on the inner cylinder, and we also know that the potential difference V between the conductors is given by
V=λ2πε0ln(ab)
Combining these expressions to eliminate λ gives
E=Vrln(ab)
The magnetic field B varies with r as
B=μ0I2πr
If the inner cylinder is at a positive potential w.r.t the outer cylinder, the electric field E is directed radially outwards. If we assume that current flows into the page along the inner cylinder and out of the page along the outer cylinder, the magnetic field will be directed clockwise as shown.

Consider an electron travelling with velocity u into the page, as a radial distance r from the axis of the cylinder. It experience an electric force Ee raidally outwards. In order for the electron to be undeviated, these forces must balance so that u=E/B. Sucstituting out expressions for E and B gives.
This expression in independent of r, so the electrons's position does not matter.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level =I (H.W)
Explore 42 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level -II (H.W)
Explore 37 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-V (SINGLE ANSWER QUESTION)
Explore 85 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
Two long concetric cylindrical conductors of radii a and b (b<a) are maintained at a potential difference V and carry equal and opposite currents l. Show that an electron with a particular velocity u parallel to the axis may travel underivated in the evacuated region between the conductors, and calculate u when a = 50 mm, b = 2.0 mm, V = 50 V and l = 100 A.
It is also possible for the electron to travel in a helical path. By regarding such a path as the combination of a circular motion perpendicular to the axis with a steady velocity parallel to the axis, indicate without detailed mathematics how this comes about.
View SolutionTwo long straight parallel conductors of length l ,separated by a distance d and each carrying a current I attract each other with a force equal to
View Solution
Knowledge Check
A and B are two thin concentric hollow conductors having radii a and 2a and charge 2Q and Q, respectively. If potential of outer sphere is 5V, then potential of inner sphere is
A20 VB10 VC253VD503VA long conductor having charge q, with charge density λ is moving with a velocity 2v parallel to its own axis. The convectional current I due to motion of conductor is
AI=λv/2BI=2λvCI=λvDI=3λvA charged spherical conductor of radius a and charge q is, surrounded by another charged concentric sphere of radius b(b>a). The potential differece between conductors is V. When, the spherical conductor of radius b is discharged completely, then the potential difference between conductor will be
AVBVabCq14πε0a−q24πε0bDNone of the above
A long coaxial cable consists of two concentric cylinders of radii a and b. The central conductor of the cable carries a steady current I and the outer conductor provides the return path of the current. Calculate the energy stored in the magnetic field of length l of such a cable
View SolutionA very long straight conductor has a circular cross- section of radius R and carries a current density J. Inside the conductor there is a cylindrical hole of radius a whose axis is parallel to the axis of the conductor and a distance b from it. Let the z-axis be the axis of the conductor, and let the axis of the hole be at x = b. Find the magnetic field
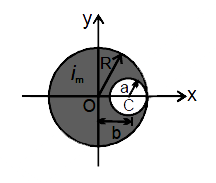
on the y = axis at y = 2R.
View SolutionA very long straight conductor has a circular cross- section of radius R and carries a current density J. Inside the conductor there is a cylindrical hole of radius a whose axis is parallel to the axis of the conductor and a distance b from it. Let the z-axis be the axis of the conductor, and let the axis of the hole be at x = b. Find the magnetic field
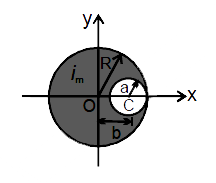
on the x=axis at x = 2R
View SolutionIn the given arrangement, the space between a pair of co-axial cylindrical conductors is evacuated. The outer cylinder, called anode, may be given a positive potential V relative to the inner cylinder.
A static homogeneous magnetic field →B parallel to the cylinder axis, directed out of plane of figure is aslo present. induced charges in the conductors are neglected.
We study the dynamics of electrons with rest mass m and charge e. The electrons are released at the surface of inner cylinder.
Consider the following two cases
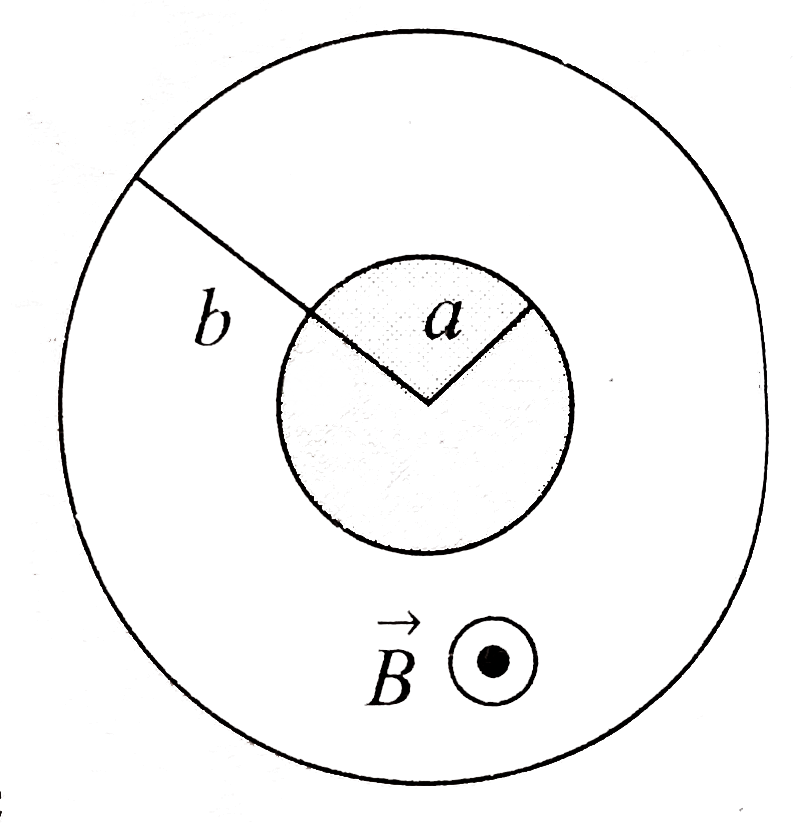
Case 1: Firstly the potential V is turned on, but →B=0. An electron with negligible velocity is ejected at the surface of inner cylinder. It is found to hit the anode.
Case 2: Now V = 0 but →B is present. An electron starts out with an initial velocity →v0 in radial direction. For magnetic field larger than critical value Bc the electron will not reach the anode.
The critical magnetic field Bc is given by
View SolutionIn the given arrangement, the space between a pair of co-axial cylindrical conductors is evacuated. The outer cylinder, called anode, may be given a positive potential V relative to the inner cylinder.
A static homogeneous magnetic field →B parallel to the cylinder axis, directed out of plane of figure is aslo present. induced charges in the conductors are neglected.
We study the dynamics of electrons with rest mass m and charge e. The electrons are released at the surface of inner cylinder.
Consider the following two cases
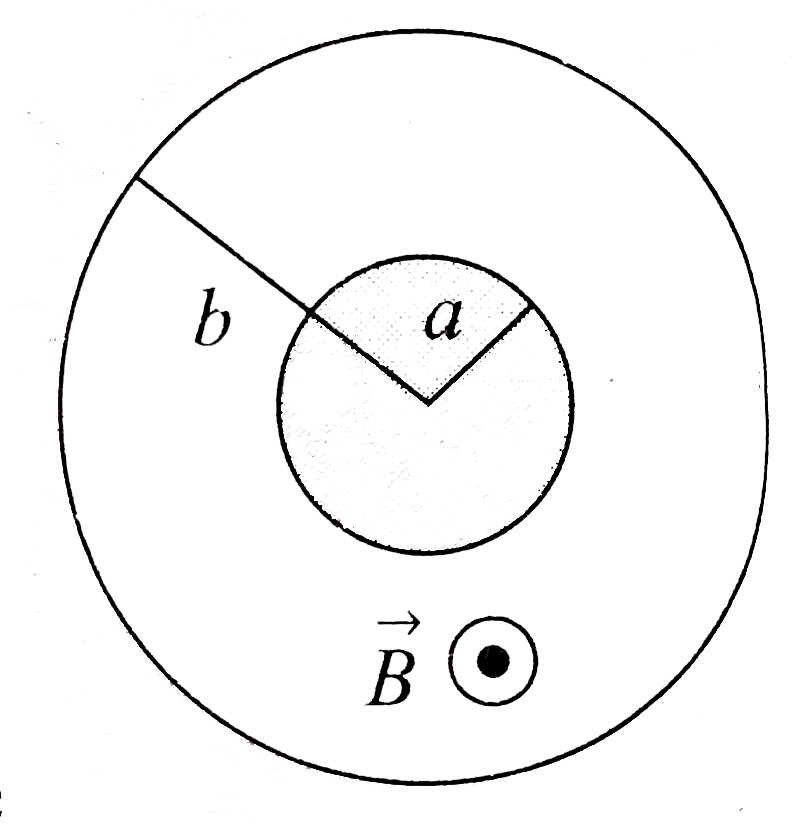
Case 1: Firstly the potential V is turned on, but →B=0. An electron with negligible velocity is ejected at the surface of inner cylinder. It is found to hit the anode.
Case 2: Now V = 0 but →B is present. An electron starts out with an initial velocity →v0 in radial direction. For magnetic field larger than critical value Bc the electron will not reach the anode.
Considering the case 1, the trajectory of electron will be
View Solution

