There are two parallel current carrying wires X and Y as shown in figure. Find the magnitude and direction of the magnetic field at points, P, Q and R.
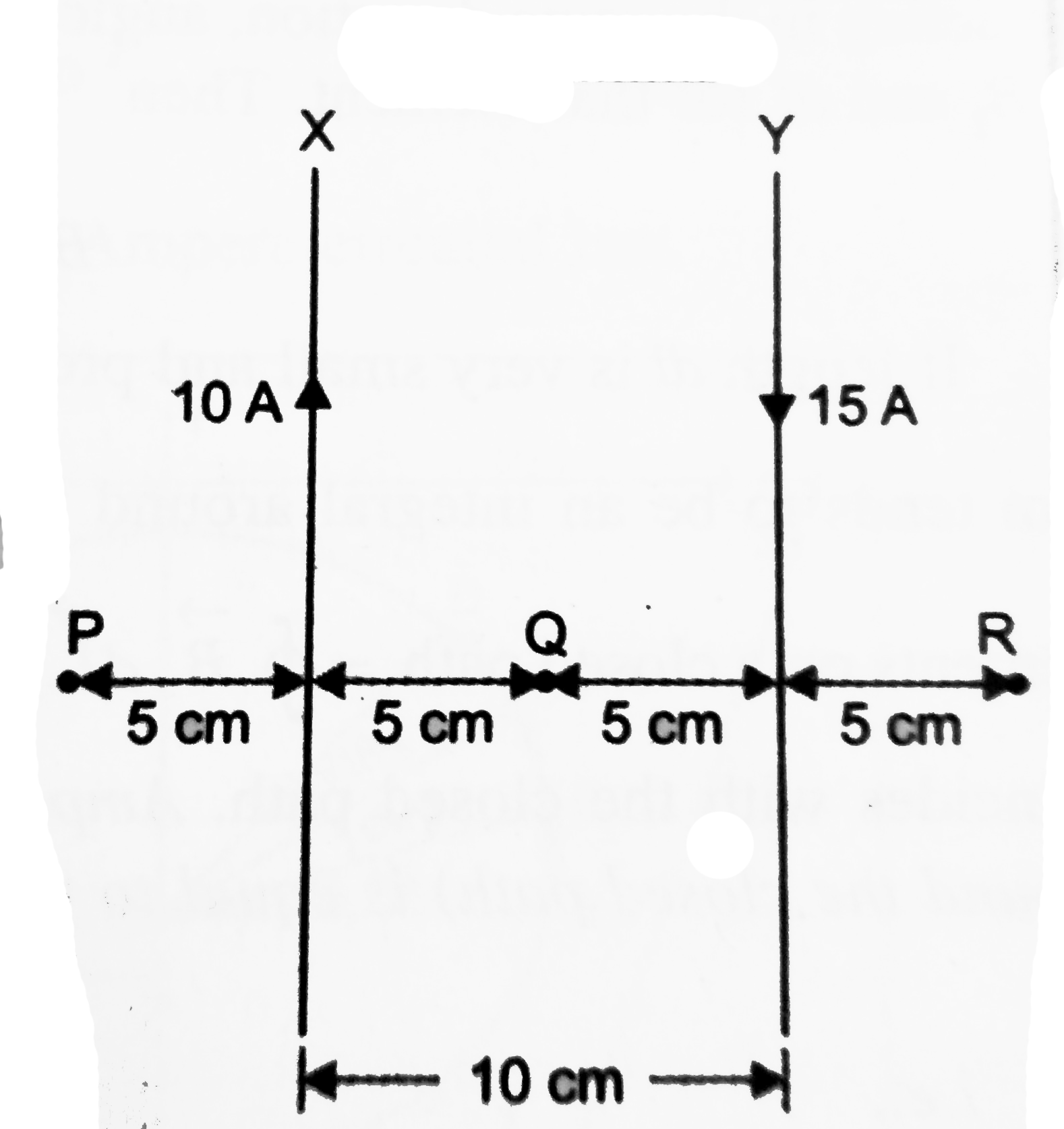
Here, I1=10,I2=15A,r=5cm=5×10−2m Let ˆn be the unit vector perpendicular to the plane of paper unwards.
The magnetic field at P due to current in wire X is
→B1=μ04π2I1rˆn=10−72×105×10−2ˆn=4×10−5ˆnT
The magnetic field at P due to current in wire Y is
→B2=μ04π2I2(r+r+r)(−ˆn)=10−7=2×1515×10−2(−ˆn)=−2×10−5T
The resultant magnetic field at P is
→BP=→B1+→B2=(4×10−5)ˆn−(2×10−5)ˆn=2×10−5Tˆn
=2×10−5T acting normally outwards.
At point Q, both →B1 and →B2 will be acting normally inwards. So
→BQ=→B1+→B2=μ04π2×105×10−2(−ˆn)+μ04π2×155×10−2(−ˆn)
=[10−7×205×10−2+10−7×305×10−2](−ˆn)=(4×10−5+6×10−5)(−ˆn)
=10−4T acting normally inwards.
At point R, →B1 will be acting normally inwards and →B2 will be acting normally outwards. So,
→BR=→B1+→B2=10−7×2×10(5+5+5)×10−2(−ˆn)+10−7×2×20(5×10−2)(ˆn)
=(−43×10−5+8×10−5)(ˆn)=203×10−5T, acting normally outwards
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Conceptual Problems (d)
Explore 2 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Very Short Answer Questions (a)
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
In the figure are shown two long parallel current carrying wires I and II. Find the magnitudes and directions of the magnetic field induction at the point P, Q and R in the plane of paper.

View SolutionFig shows two current-carrying wires 1 and 2. Find the magnitudes and directions of the magnetic field at points P,Q and R.

View Solution
Knowledge Check
A current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is
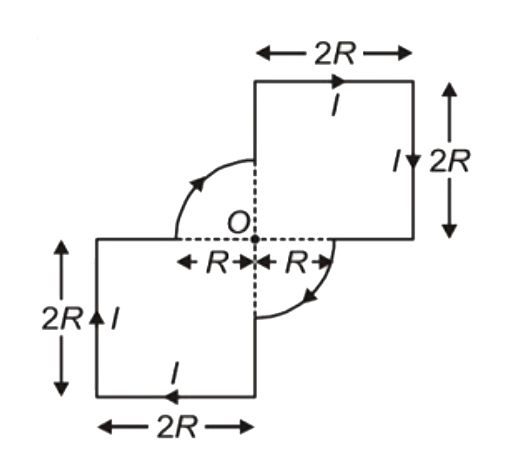 Aμ0I4RBμ0I2R(1+√2π)Cμ0I4R(1+√2π)Dμ04R(1+2√2π)
Aμ0I4RBμ0I2R(1+√2π)Cμ0I4R(1+√2π)Dμ04R(1+2√2π)
There are two parallel current carrying wires X and Y as shown in figure. Find the distance of a point from wire X, where the resultant magnetic field is zero.
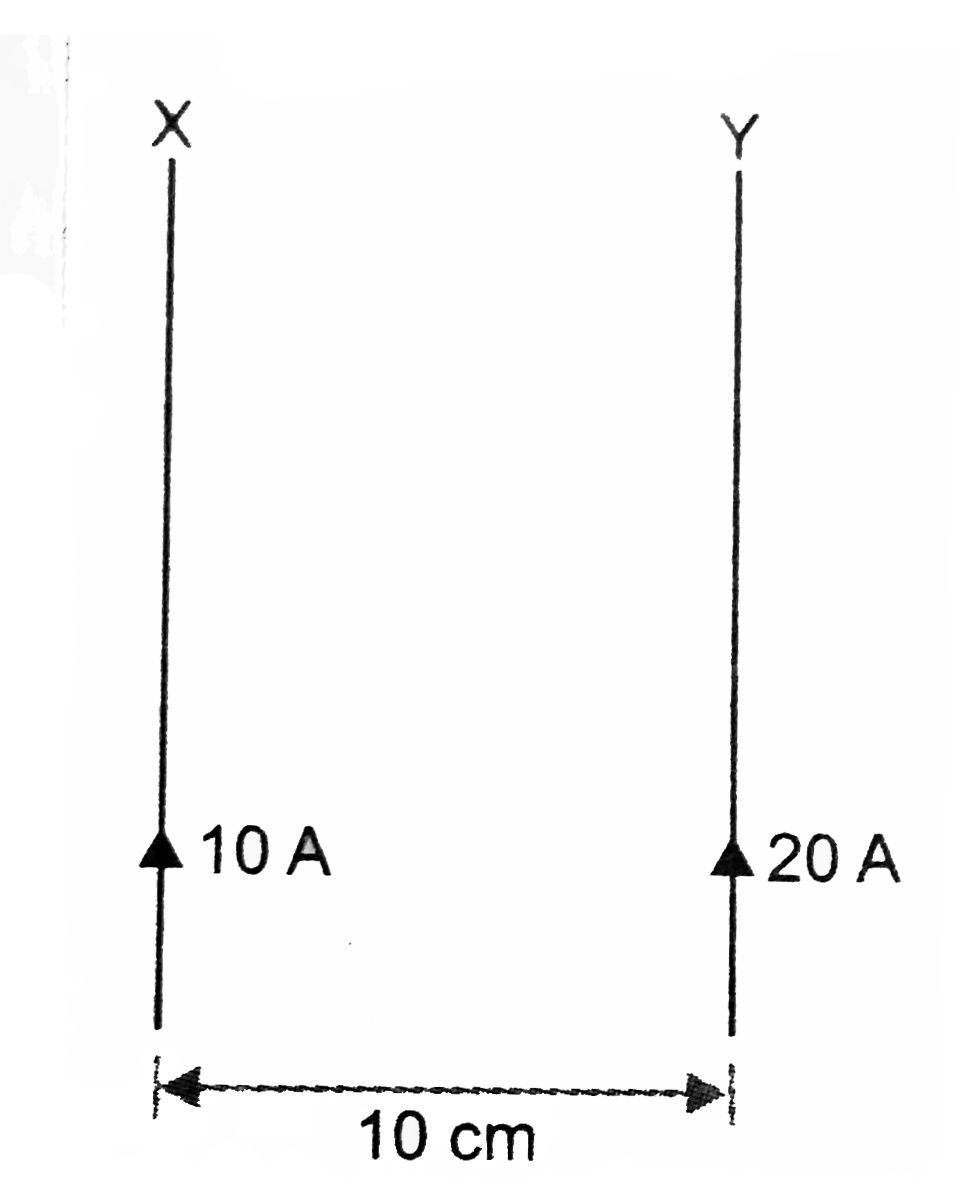
View Solution(a) Draw the pattern of magnetic field lines for a circular coil carrying current.
(b) Two identical planes such that they have a common centre at P as shown in the figure. Find the magnitude and direction of the net magnetic field at the point P due to the loops
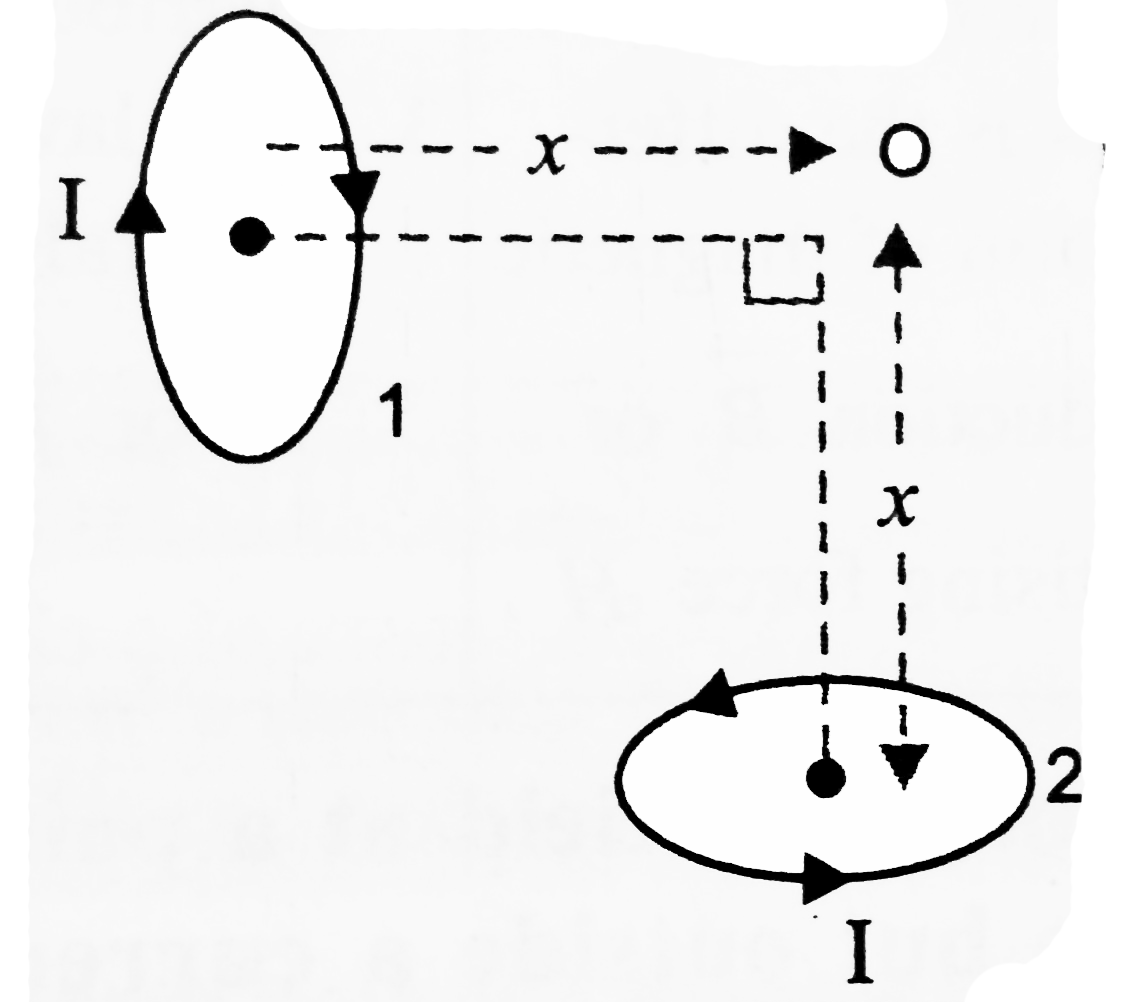
View SolutionTwo small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.

View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
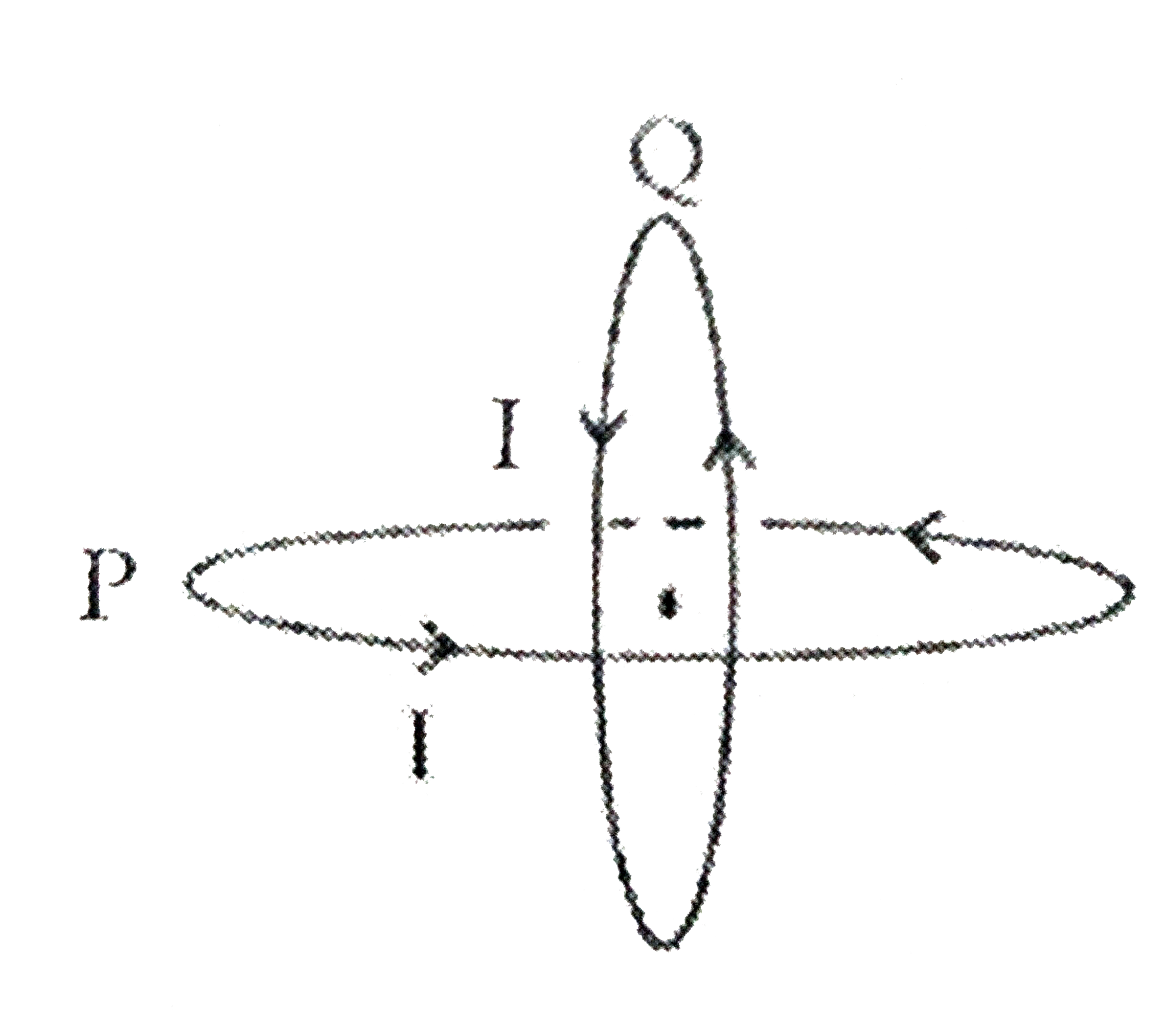
View SolutionTwo long parallel wires are carrying currents as shown
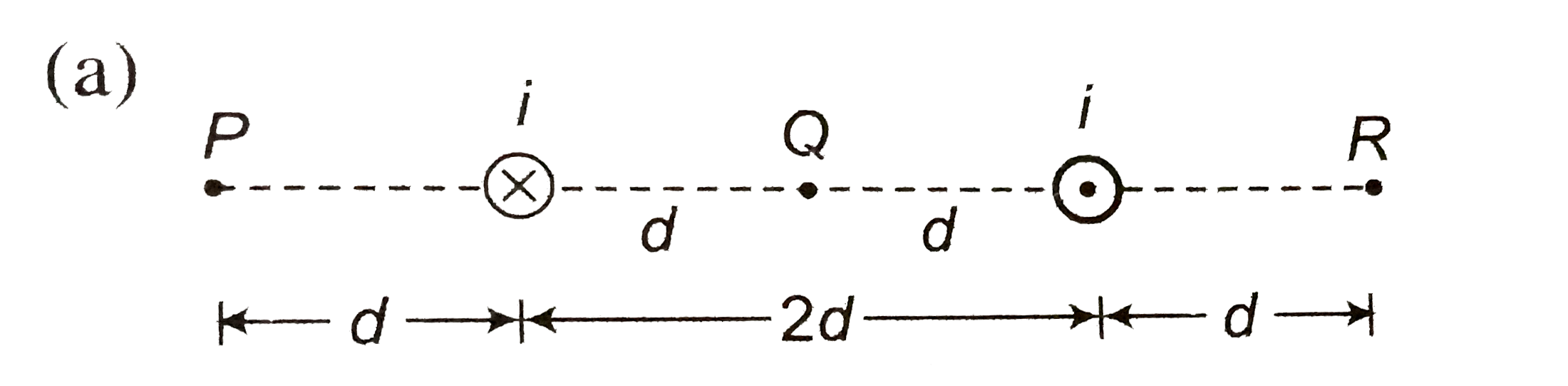
Find magnitude and direction of magnetic field at P,Q and R.
(b) (i)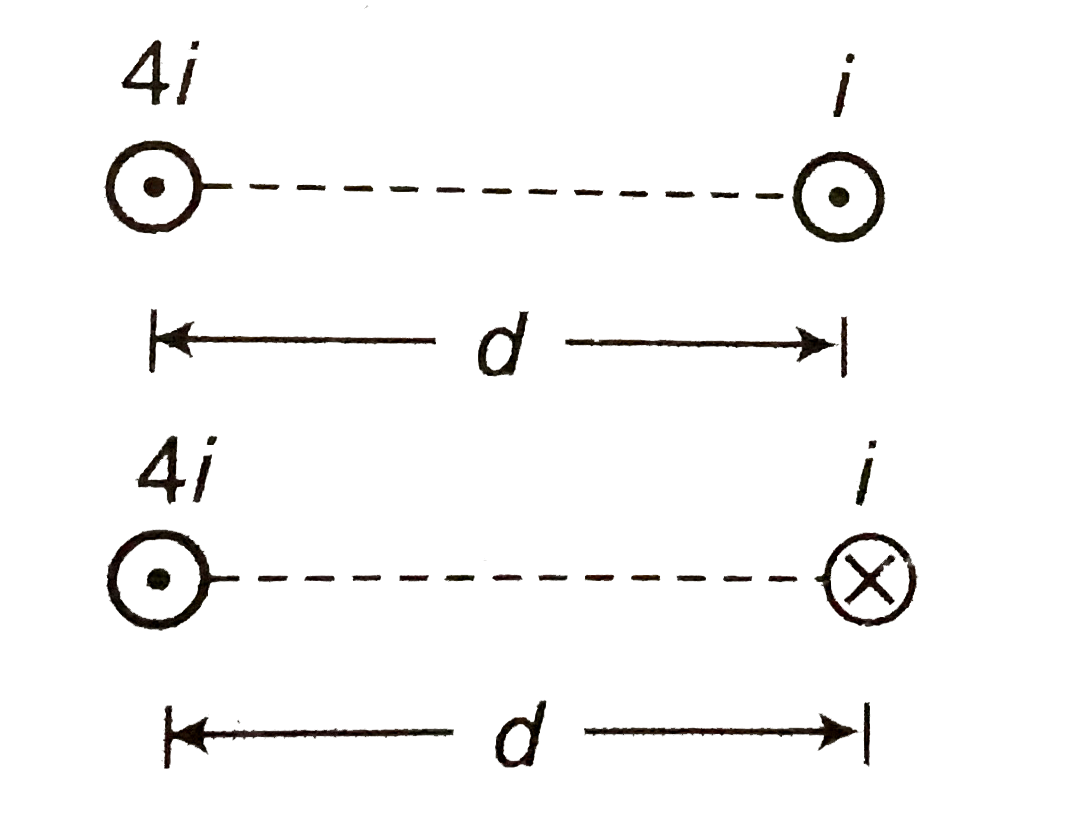
(ii)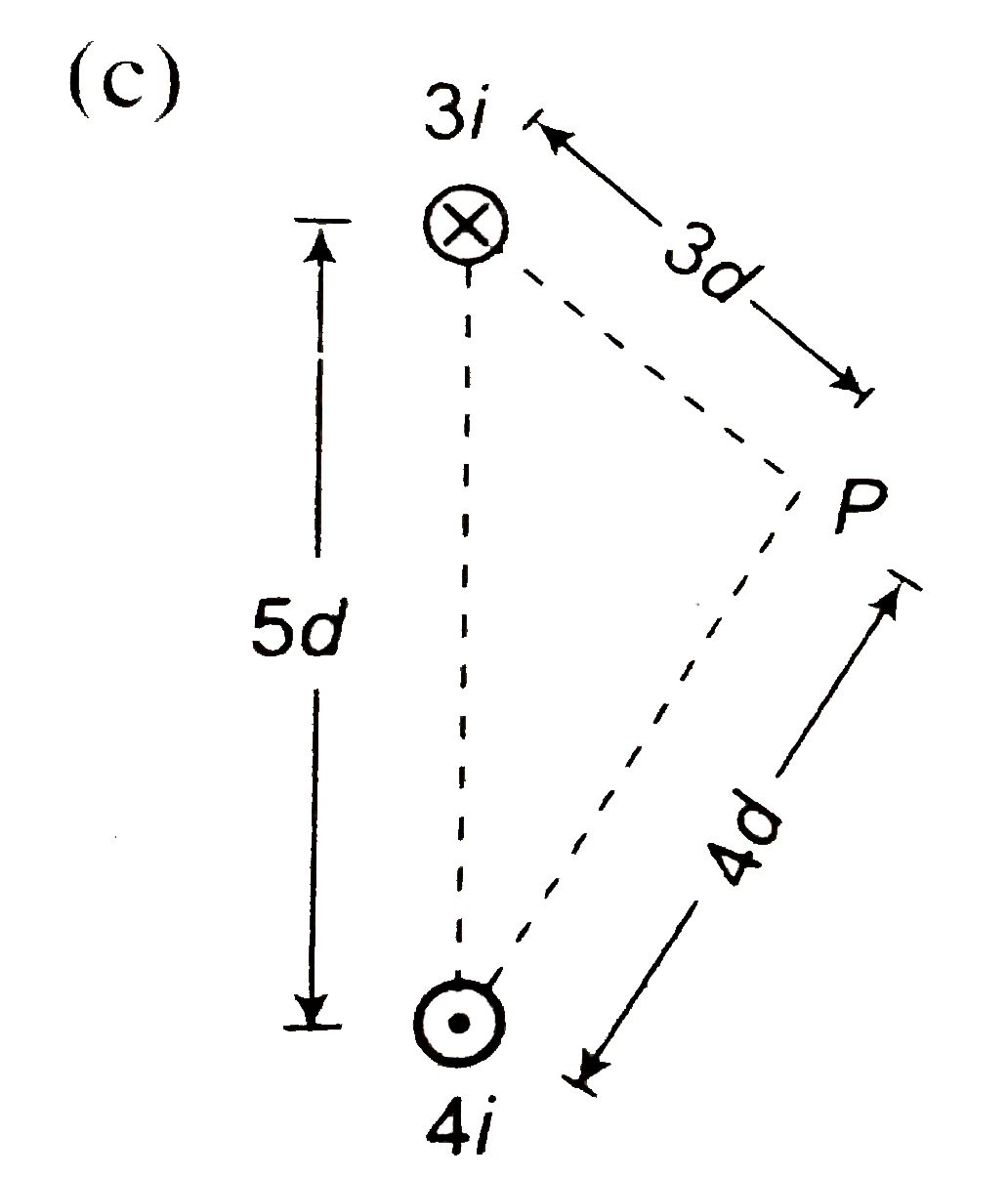
At what distance from left wire, magnetic field is zero on the line joining the wires.
Find magnitude of magnetic field at P.
(d) Two straight infinitely long and thin parallel wires are spaced d distance apart and carry a current i each. find the magnetic field at a point distance d from both wires when the currents are in the (i) same and (ii) opposite directions.
View Solution(a) Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
(b) A straight wire carrying a current of 5 A is bent into a semicular arc of radius 2 cm as shown in the fig. FInd th magnitude and direction of the magnetic field at the centre of the arc.

View Solution

