A ball is dropped from a height h onto a floor and rebounds to a height h/6. The coefficient of restitution between the ball and the floor is
12
14
23
1√6
The correct Answer is:B
To find the coefficient of restitution (E) between the ball and the floor, we can follow these steps:
Step 1: Understand the Problem
The ball is dropped from a height h and rebounds to a height h6. We need to find the coefficient of restitution, which is defined as the ratio of the relative speed after the collision to the relative speed before the collision.
Step 2: Identify Initial and Final Velocities
- When the ball is dropped from height h, its initial velocity U1 just before hitting the ground can be calculated using the equation of motion:
V21=U21+2gh
Since the initial velocity U1=0:
V21=2gh⇒V1=√2gh
- After rebounding to a height h6, the final velocity V2 just after the ball leaves the ground can be calculated similarly:
V22=U22−2g(h6)
Here, the final velocity U2=0 at the peak height:
0=U22−2g(h6)⇒U22=2gh6⇒U2=√2gh6=1√3√2gh
Step 3: Calculate the Coefficient of Restitution
The coefficient of restitution E is given by:
E=V2V1
Substituting the values we found:
E=1√3√2gh√2gh=1√3
Final Answer
Thus, the coefficient of restitution E between the ball and the floor is:
E=1√3
The ball is dropped from a height h and rebounds to a height h6. We need to find the coefficient of restitution, which is defined as the ratio of the relative speed after the collision to the relative speed before the collision.
- When the ball is dropped from height h, its initial velocity U1 just before hitting the ground can be calculated using the equation of motion:
V21=U21+2gh
Since the initial velocity U1=0:
V21=2gh⇒V1=√2gh
V22=U22−2g(h6)
Here, the final velocity U2=0 at the peak height:
0=U22−2g(h6)⇒U22=2gh6⇒U2=√2gh6=1√3√2gh
The coefficient of restitution E is given by:
E=V2V1
Substituting the values we found:
E=1√3√2gh√2gh=1√3
Thus, the coefficient of restitution E between the ball and the floor is:
E=1√3
Topper's Solved these Questions
Similar Questions
Knowledge Check
A ball falls from rest from a height h onto a floor, and rebounds to a height h/4. The coefficient of restitution between the ball and the floor is
A1√2B12C14D34A ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
Ah(1−2e2)Bh[1+e21−e2]Ch[1−e21+e2]Dhe2A ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is 12. The displacement time graph of the ball will be.
A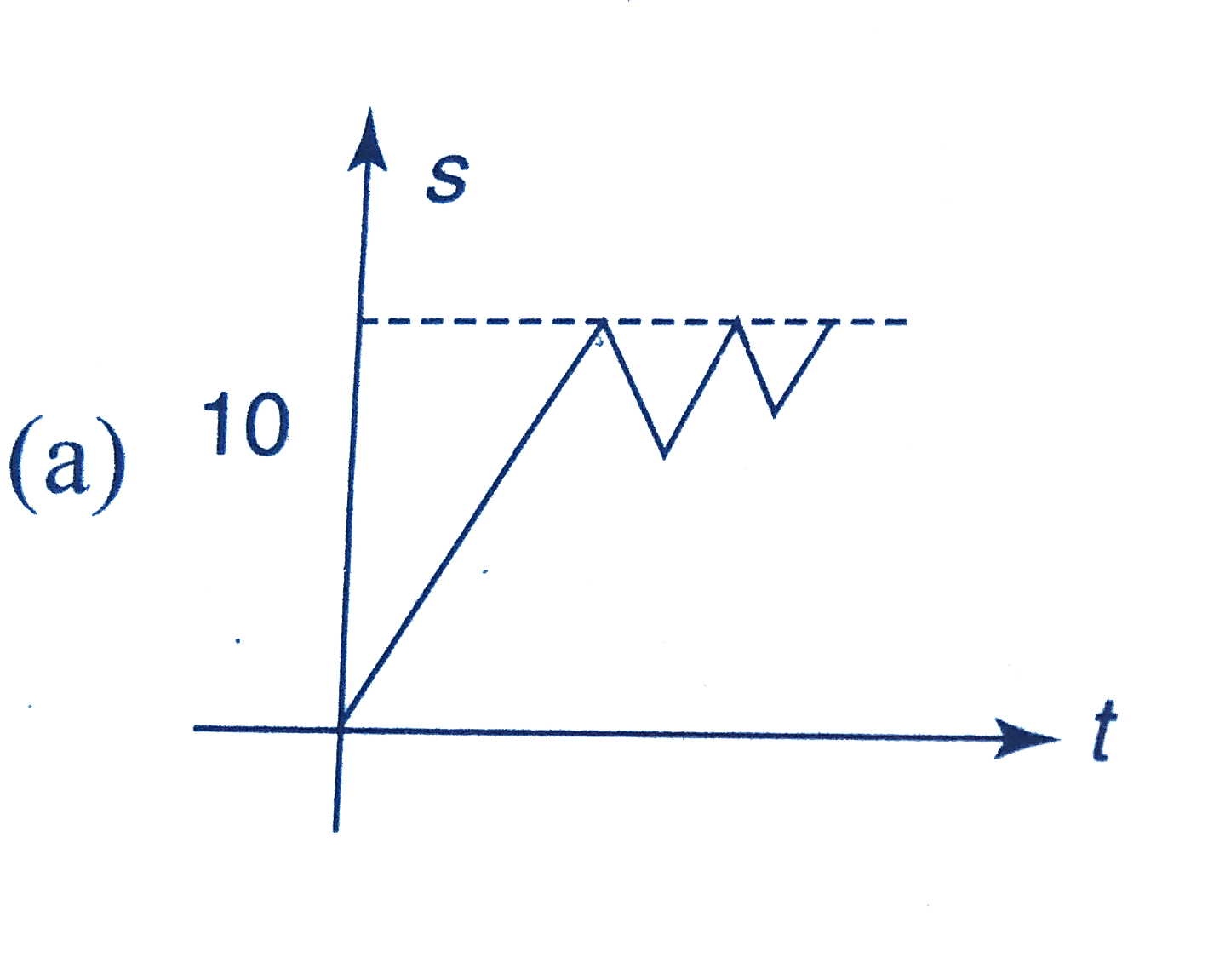 .B
.B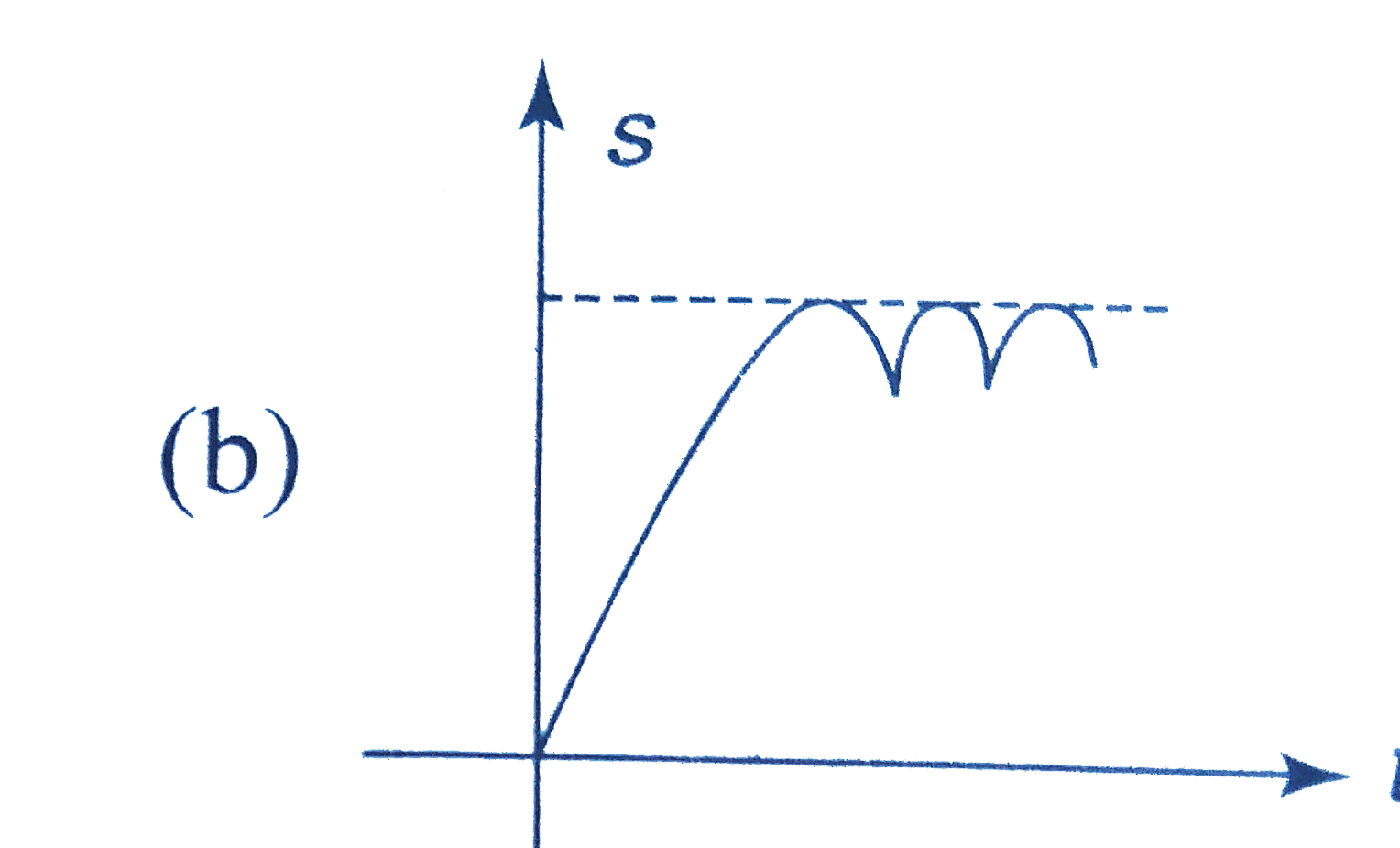 .C
.C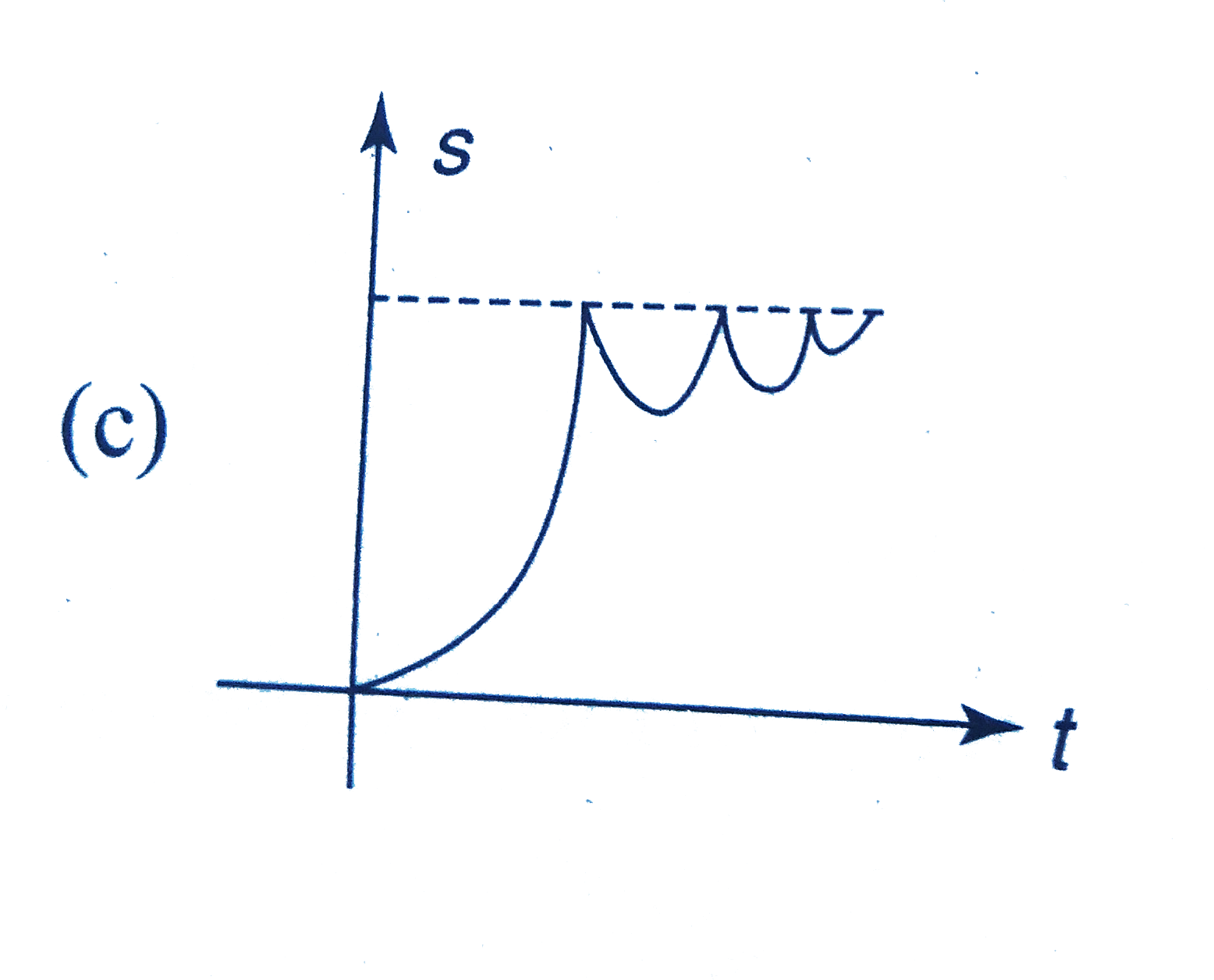 .D
.D .
.
A ball is dropped from a height of 20 m in the floor and rebounds to 1.25 m after second collision, then coefficient of restitution e is
View SolutionA particle is dropped from rest from a height h0 on a horizontal floor. The coefficient of restitution between the floor and particle is e. Maximum height attained by the particle after first rebound is
View SolutionA ball is dropped from height 5m. The time after which ball stops rebounding if coefficient of restitution between ball and ground e=1/2, is
View SolutionA ball is dropped on a horizontal surface from height h. If it rebounds upto height h2 after first collision then coefficient of restitution between ball and surface is
View SolutionA 1.0 kg ball drops vertically into a floor from a height of 25 cm . It rebounds to a height of 4 cm. The coefficient of restitution for the collision is
View Solution

