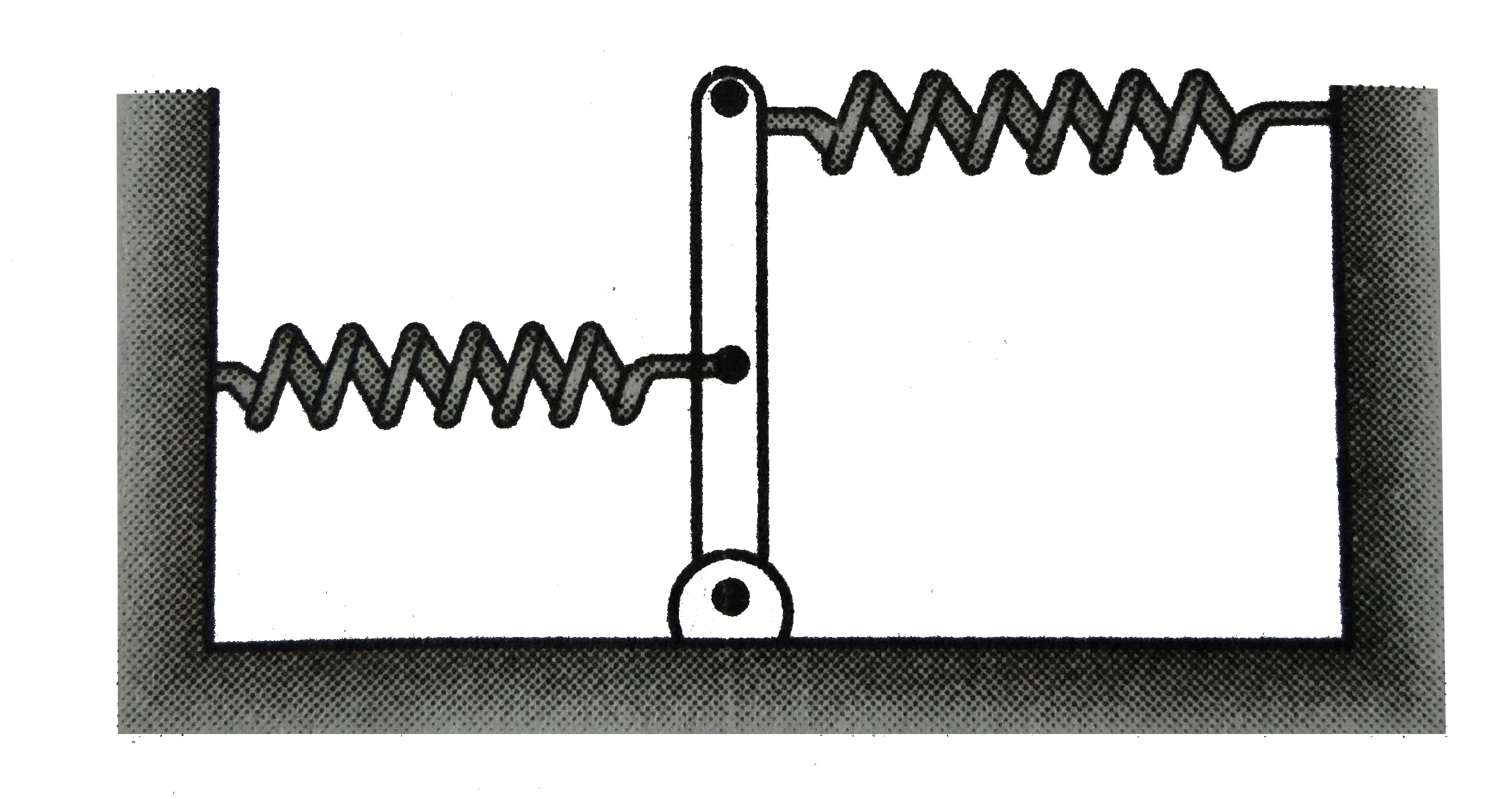
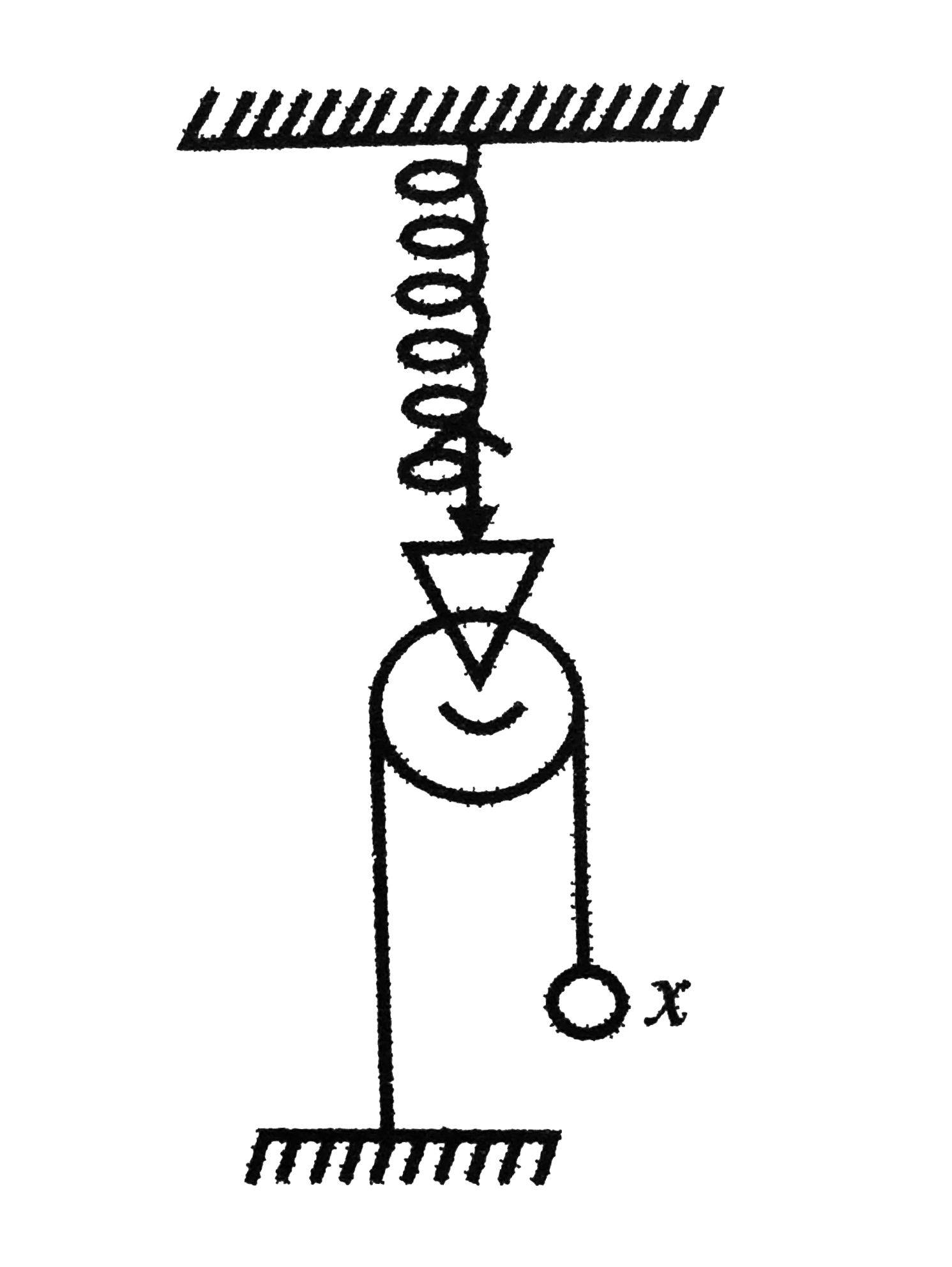
A block of mass m is attached to one end of a light inextensible string passing over a smooth light pulley B and under another smooth light pulley A as shown in the figure. The other end of the string is fixed to a ceiling. A and B are held by spring of spring constants k1 and k2. Find angular frequency of small oscillations of small oscillations of the system.

√Ka+Kbm
√KaKb(Ka+Kb)m
√KaKb4m(Ka+Kb)
√4KaKb(Ka+Kb)m
The correct Answer is:C
Let T be the tension in the cord and xa and xb the displacements of pulleys A and b respectively. Now assume that pulley B is fixed, then extension of spring xb=x2 or x=2xb. Similarly if we imagine that pulley A is fixed, x=2xa.But neither pulley B nor pulley A is fixed. ∴x=2xa+2xb....(1)
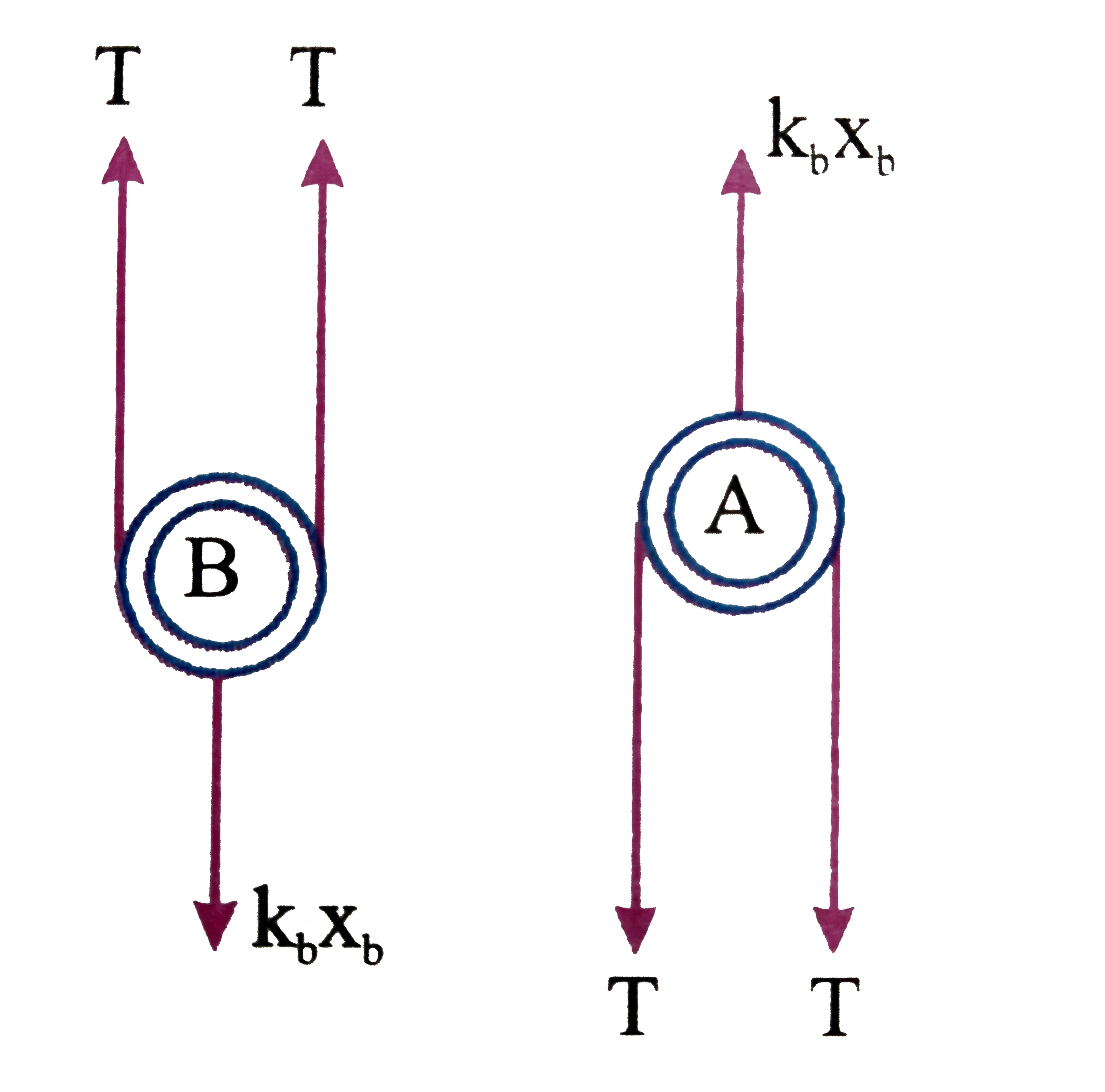
From free body diagram of pulleys,
2T=kbxb...(2) or 2T=kaxa...(3)
If keq denotes equivalent spring constant,
Tkeq=x=2xa+2xb From equations (2) and (3)
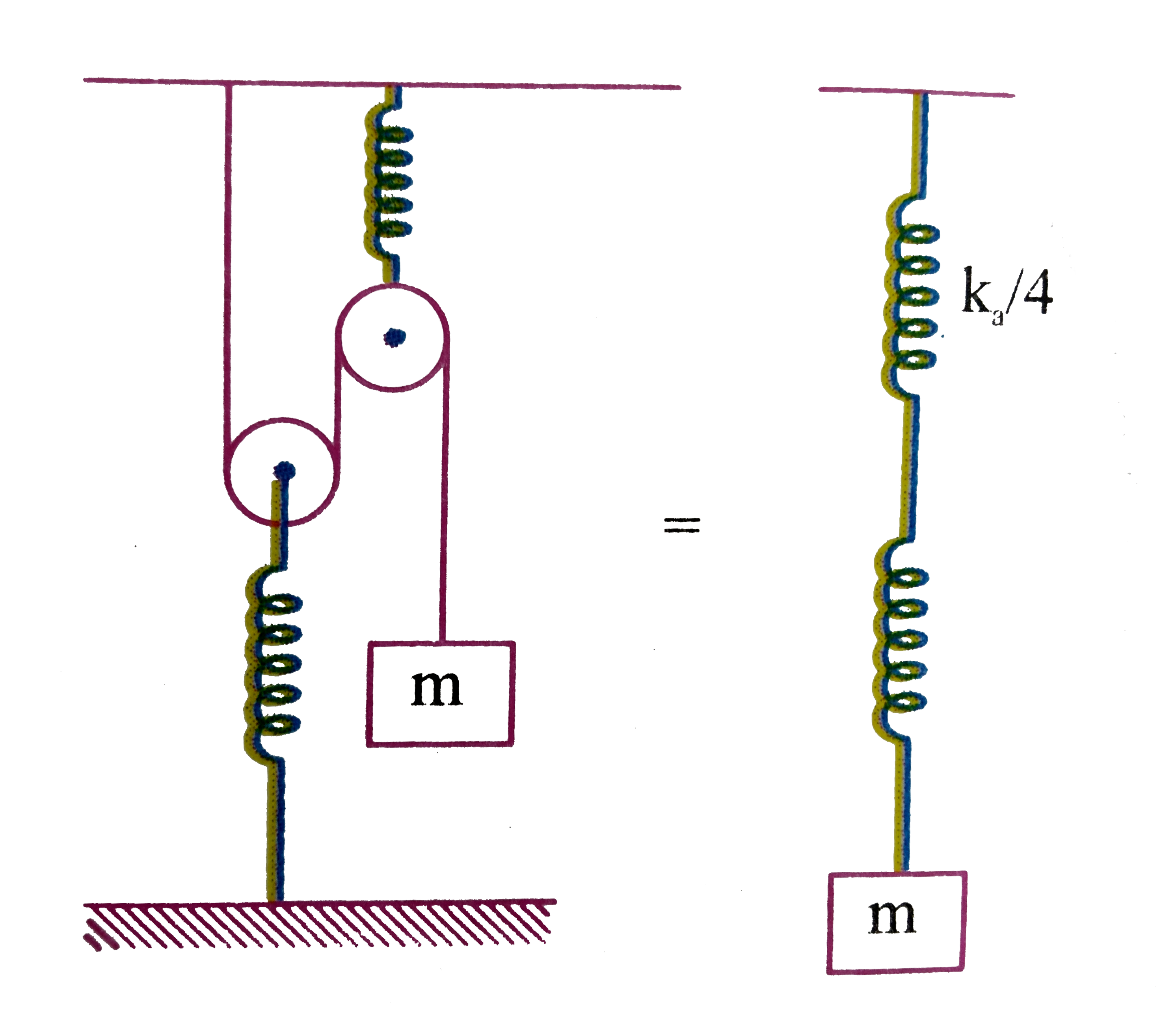
xa=2Tka and xb=2Tkbi.e.,keq=14(1ka+1kb)
Hence ω=√keqm=√kakb4m(ka+kb)
2nd Method
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage
33 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
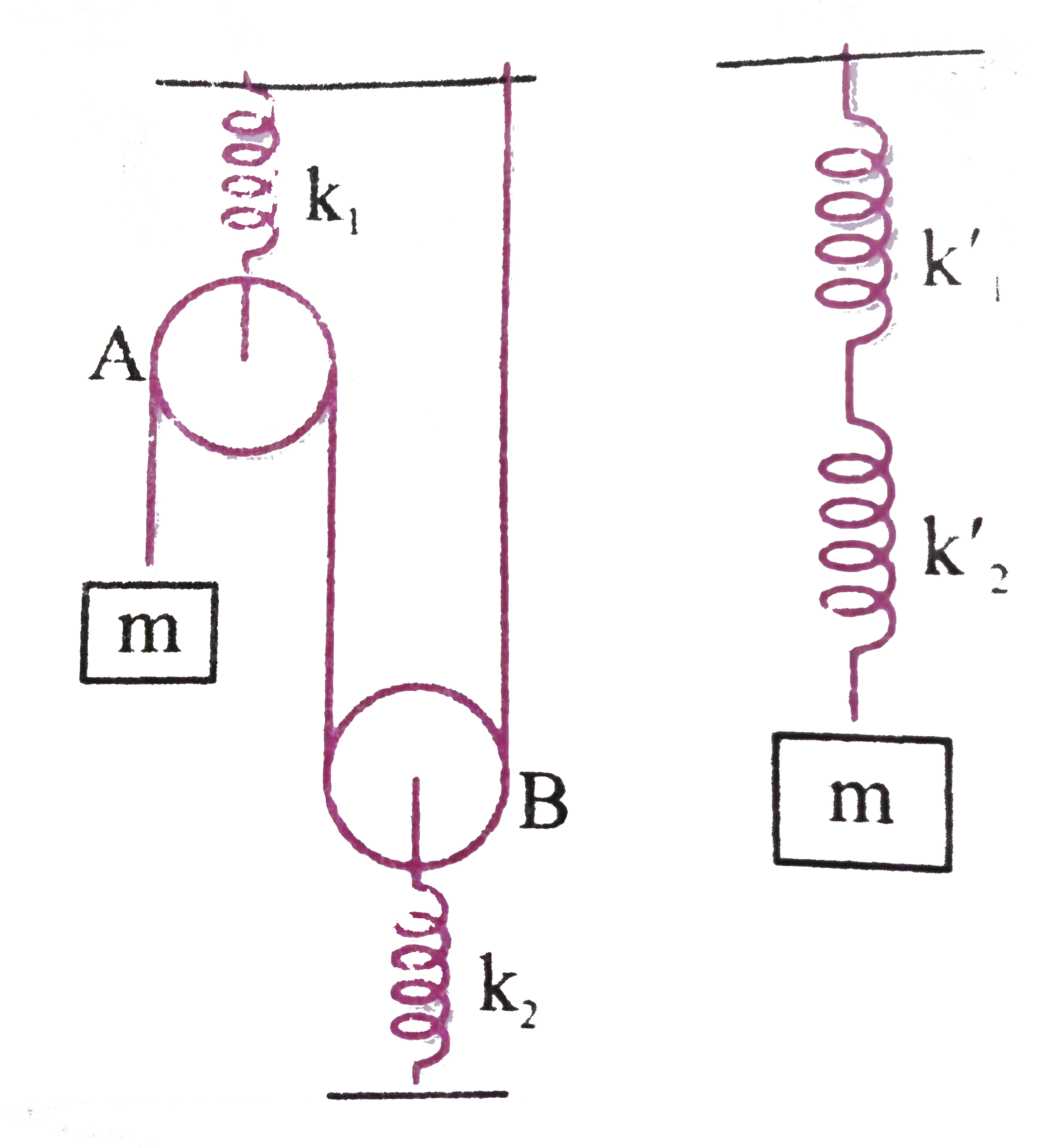
A block of mass m is attached to one end of a light intextensible string passing over a smooth light pulled A and under another smooth light pulled B as shown in Fig. The other end of a springs is fixed to a ceiling. A and B are held by spring of force constant k1 and k2. Find the period of small oscillations of system.
View Solution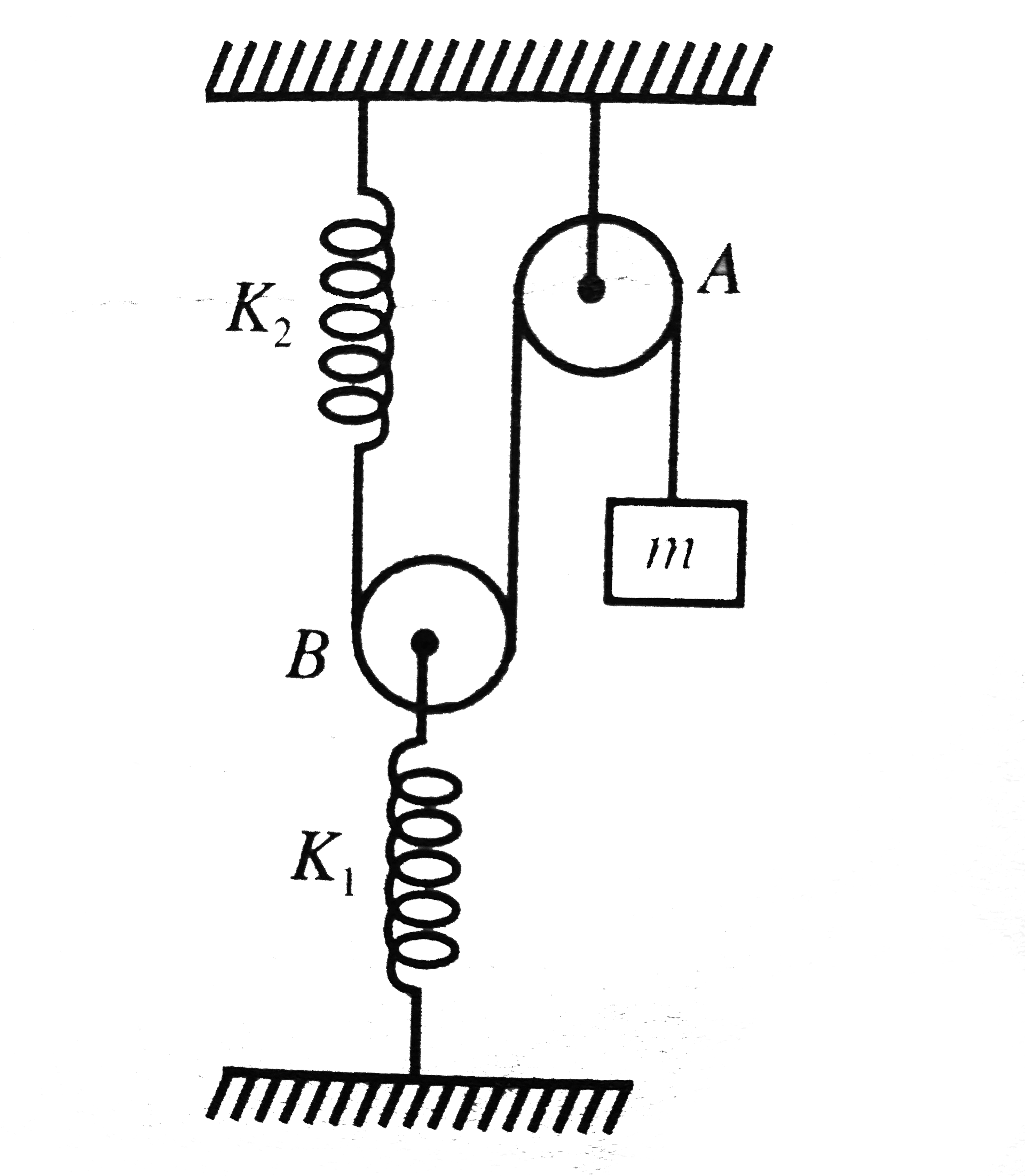
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
View Solution
Knowledge Check
Two masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
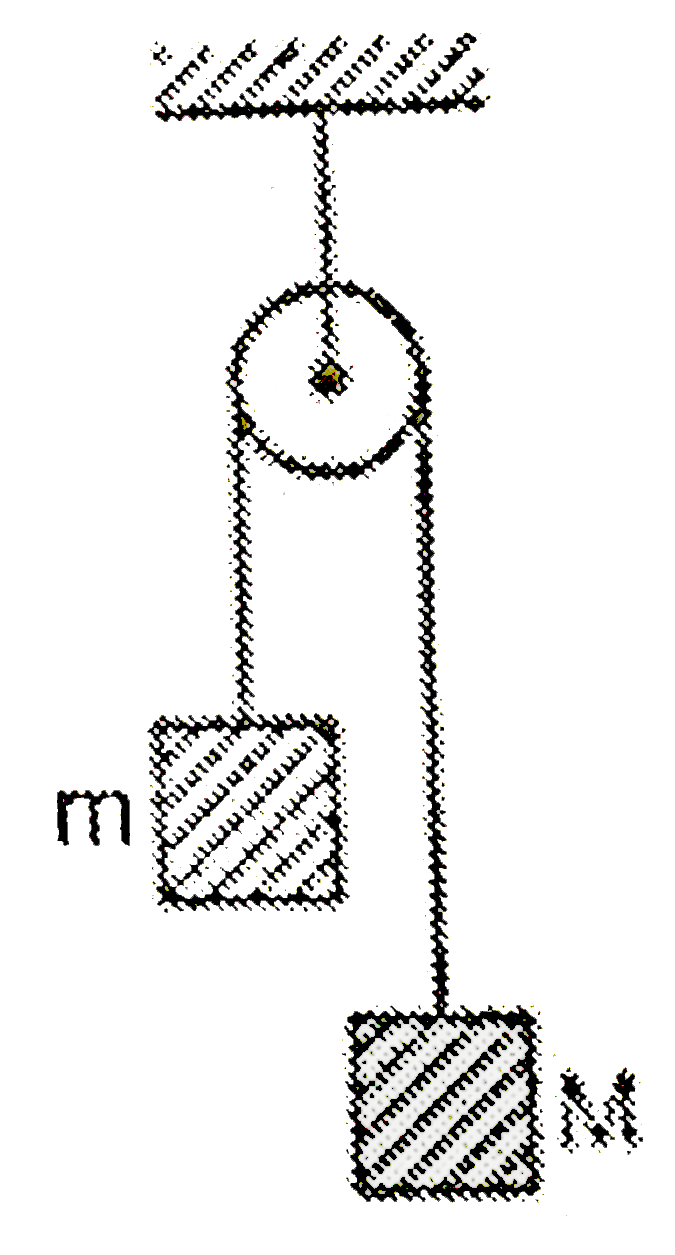 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)gTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
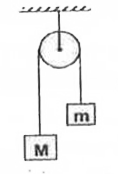 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the aboveTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
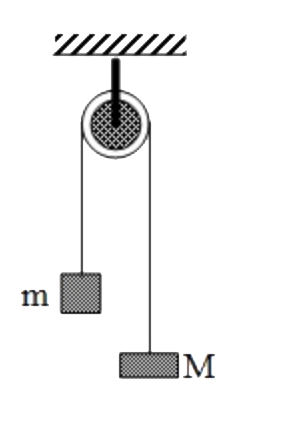 Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero
Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero
A rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.
View SolutionA body of mass m hangs by an inextensible string that passes over a smooth mass less pulley that is fitted with a light spring of stiffness k as shown in figure. If the body is released from rest and the spring is released, calculate the maximum elongation of the spring.
View SolutionTwo bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View SolutionTwo weights w1 and w2 are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up at an acceleration g , the tension in the string will be
View Solution
