A ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is α.The thread is displaced through a small angle β away from the vertical and the ball is released. Find the period of oscillation of pendulum.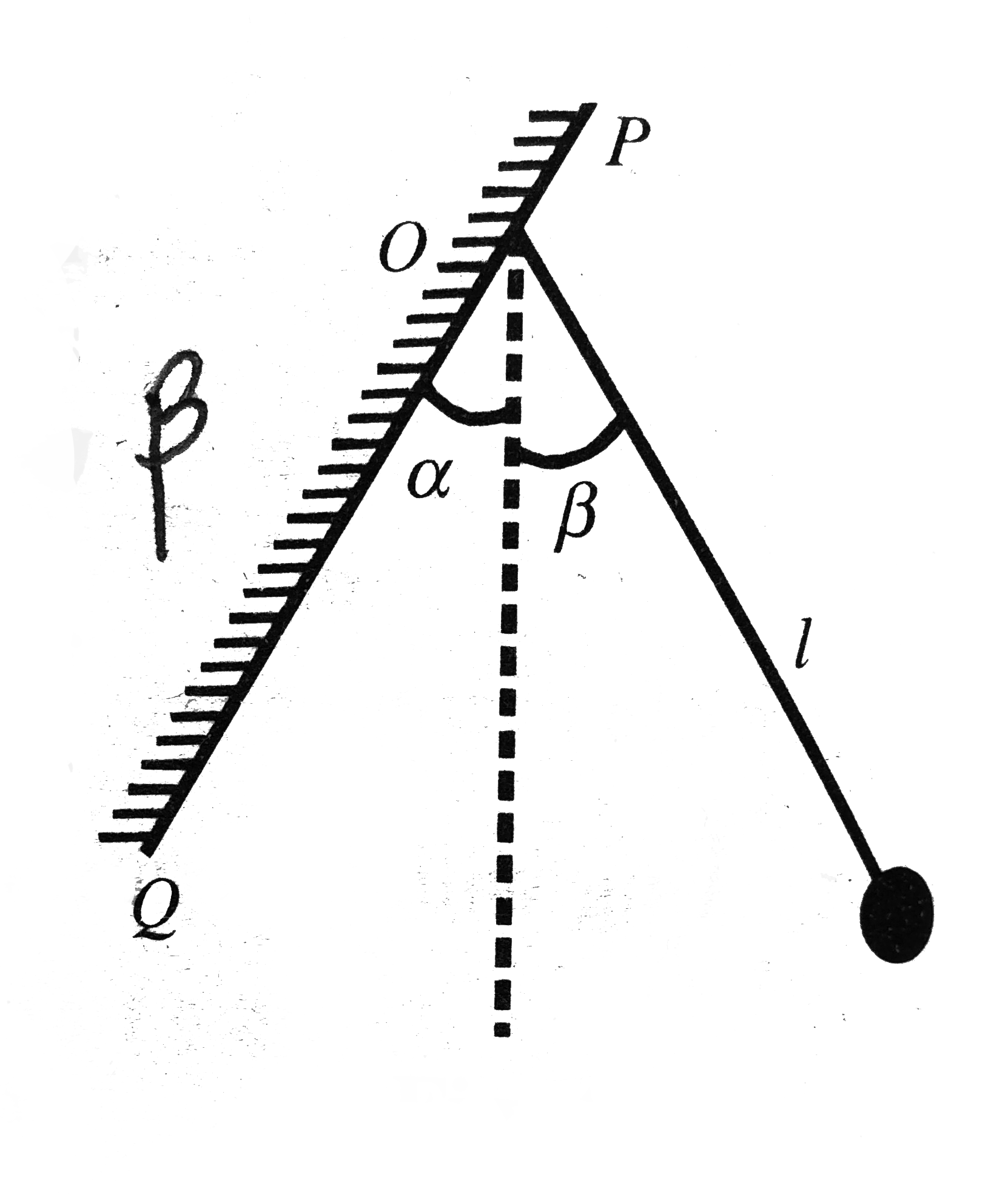 
Consider both cases
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.
2π√lg+2√lg.cos−1(αβ)
2π√lsinαg
2π√lsinαgcosβ
2π√lg−2√lg.cos−1(αβ)
The correct Answer is:D
If α<β, the ball collides with the wall and rebounds with same speed. The motion of ball from A to Q is one part of a simple pendulum. Time period of ball =2(tAQ). Consider A as the starting point (t=0).
Equation of motion is x(t)=Acosωt
x(l)=lβcosωt, because amplitude =A=lβ
time form A to Q is the time t when x becomes
−lα.⇒−lα=lβcosωt
⇒t=tAQ=1/ωcos−1(−αβ)
The return path from Q to A will involve the same time interval. Hence time epriod of ball =2tAQ
2ωcos−1(−αβ)=2√lgcos−1(−αβ)=2π√lg−2√lgcos−1(αβ).
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I2videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage33videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
A ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is (a)the thread is displacement through a small angle away from the vertical and (b) the ball is released. Find the period of oscillation of pendulum. Consider both cases
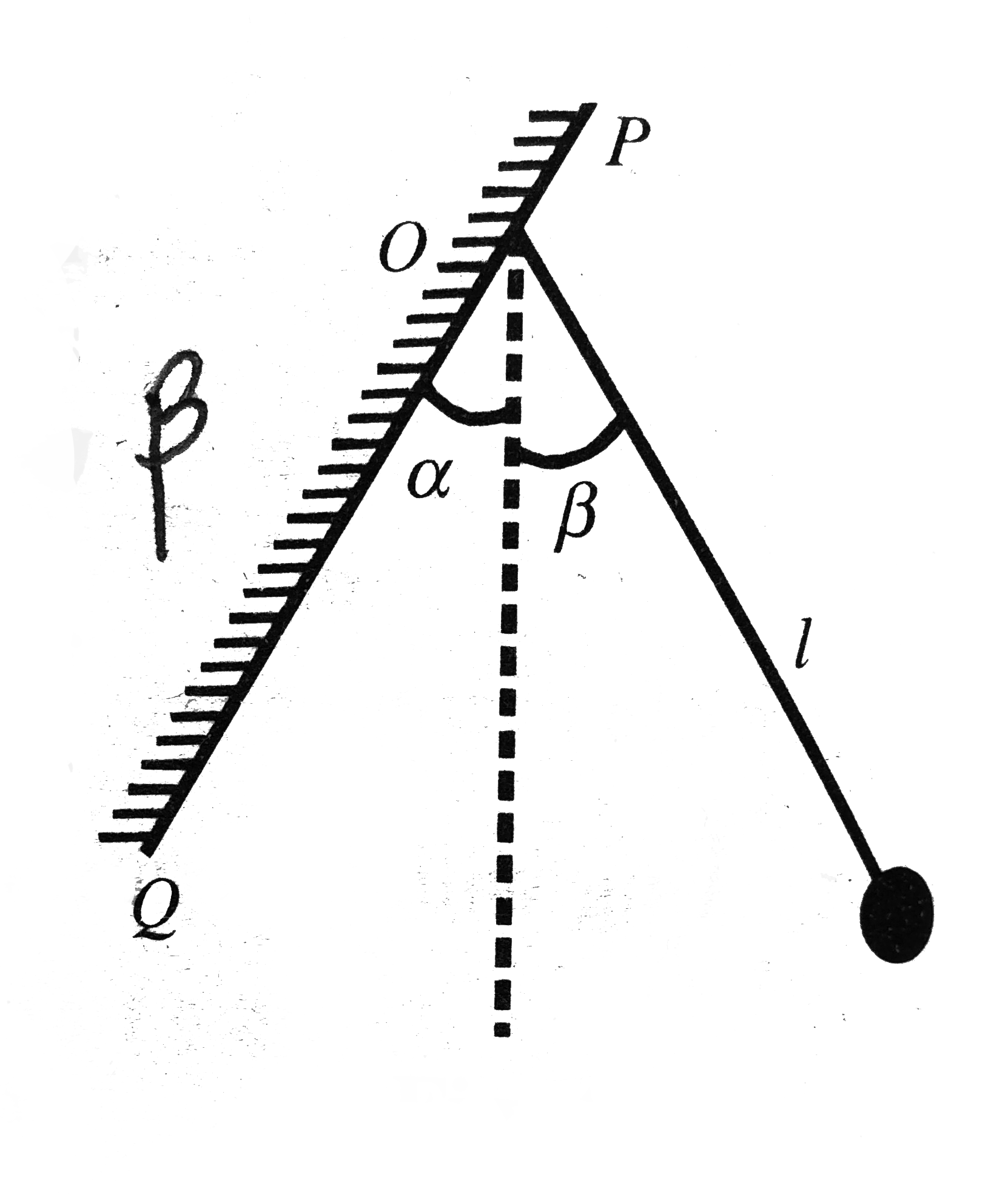
a. α>β
b. α<β
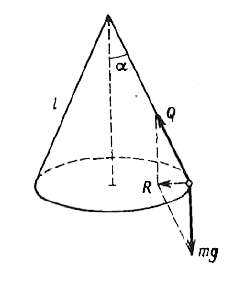
Assuming that any impact between the wall and the ball is elastic.View SolutionFind the period of revolution of a conical simple pendulum whose thread of length l makes an angle α with the vertical (Fig).
View Solution
Knowledge Check
- Question 1 - Select One or More
A small sphere of mass m suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then
ATotal acceleration of sphere as a function of θ measured from the vertical is g√1+3cos3θBThread tension as a function of θ measured from the vertical is T=3mgcosθCThe angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally is cos−11/√3.DThe thread tension at the moment when the vertical component of the sphere's velocity is maximum will be mg. - Question 2 - Select One
Aa simple pendulum is suspended from the ceiling of a vehicle which moves down an inclined plane o inclination Θ. The period of oscilation of the pendulum is
A2π√LgcosθB2π√LcosθgC2π√LgsinθD2π√Lsinθg - Question 3 - Select One
A ball is thrown at angle α(90∘>α>θ) on inclination plan as shown in figure. The minimum speed of the ball during the motion is:
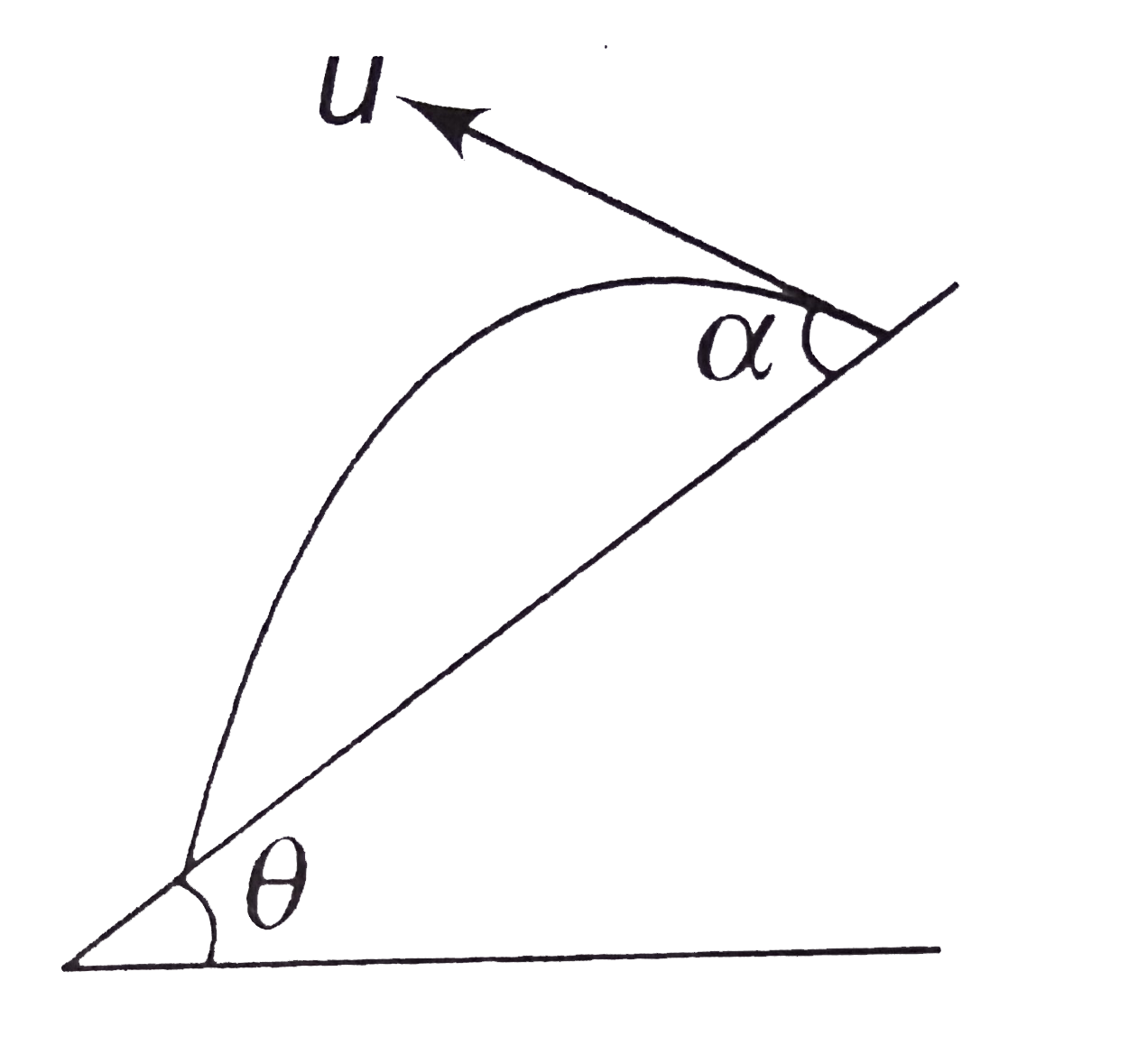AucosαBucosθCucos(α−θ)Dzero
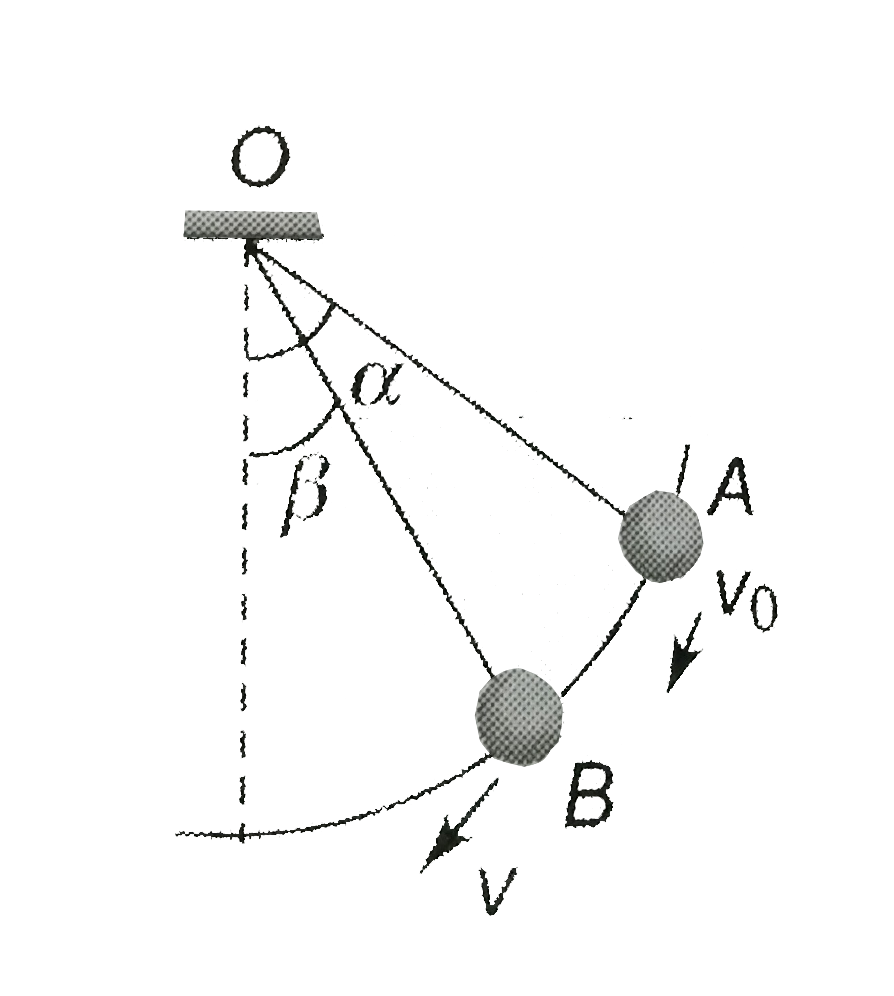
A ball attached to a string length L is oscillating line a simple pendulum. Find v in terms of v0 L α and β.View SolutionA small ball is suspended from point O by a thread of length l. A nail is driven into the wall at a distance of l/2 below O, at A. The ball is drawn aside so that the thread takes up a horizontal position at the level of point O and then released. Find
a. At what angle from the vertical of the ball's trajectory, will the tension in the thread disappear?
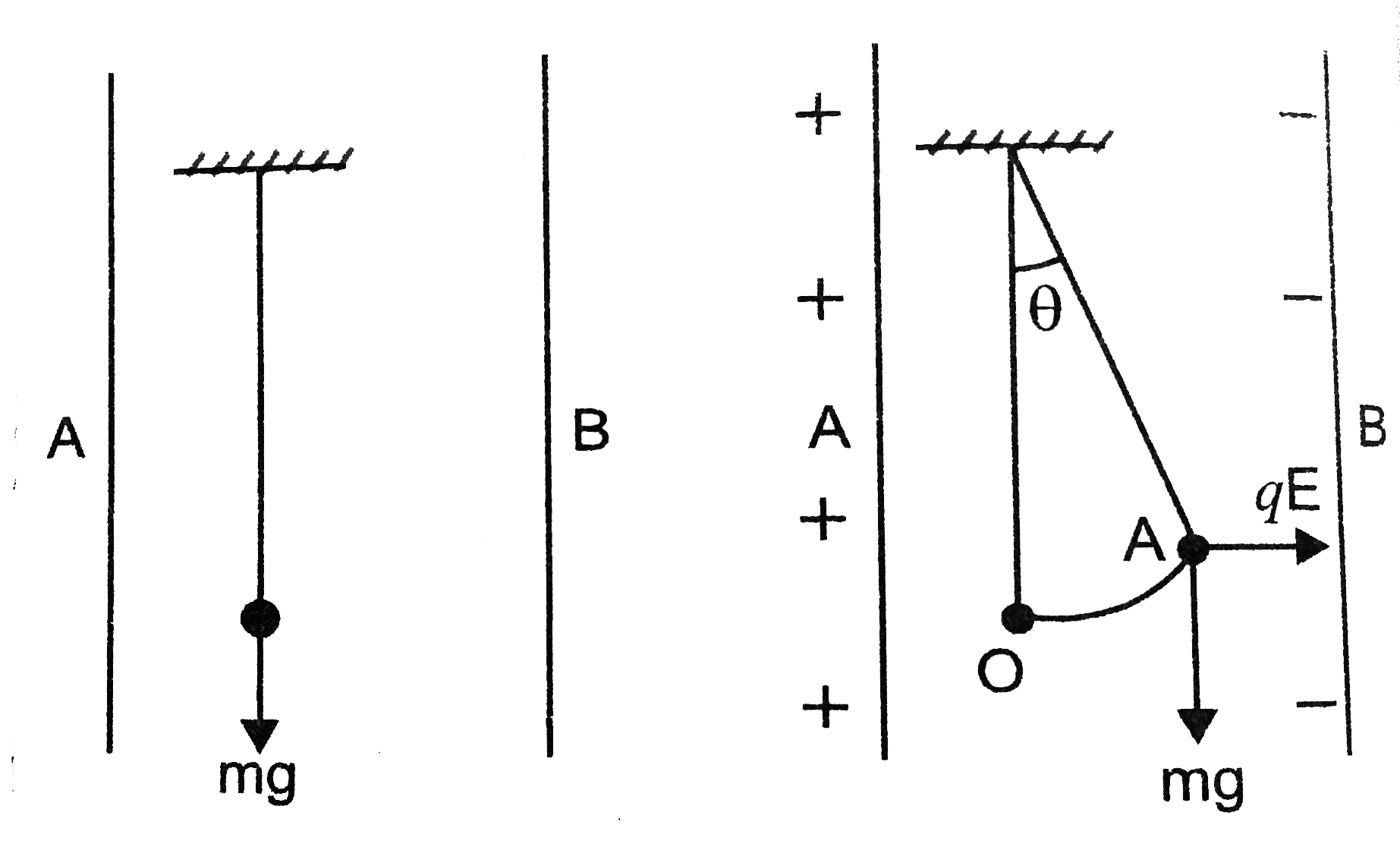
b. What will be the highest point from the lowermost point of circular track, to which it will rise?View SolutionA metal ball suspended from a long thread is held between the plates of a capacitor , as shown in Fig, How will the oscillations of this pendulum change, if the ball and the plates of two capacitor are charged ?
View SolutionA ball is thrown upwards from the top of an incline with angle of projection θ with the vertical as shown. Take θ=60∘ and g=10m/s2 . The ball lands exactly at the foot of the incline.
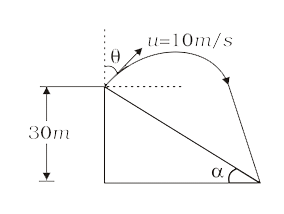
The angle of inclination of incline α is:View SolutionA ball is thrown upwards from the top of an incline with angle of projection θ with the vertical as shown. Take θ=60∘ and g=10m/s2 . The ball lands exactly at the foot of the incline.
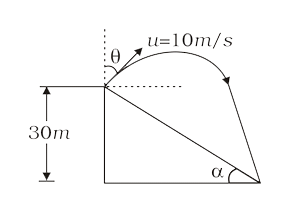
The time of flight of the ball is:View Solution