A solid sphere of radius R is floating in a liquid of density σ with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
12π√3g2R
12π√2R3g
12π√Rg
12π√5g3R
The correct Answer is:A
Half of the volume of sphere is submerged. For equilibrium of sphere, Weight =upthrust
∴Vrxg=V2(rL)(g),rs=ρL2..(1)
When slightly pushed downwards by x, weigth will remain as it is while upthrust will increase. The increased upthrust will become the net restoring force (upwards).
F=−(extra upthrust)
=−(extra volume immersed)(rL)(g)
or ma=−(πR2)xrL(a=acceleration)
∴43πR3(ρ2)a=−(πR2)xrLg(a=acceleraiton)
∴a=−(3g2R)x as the given motion is simple harmonic
Frequency of oscillation, f=12π√∣∣ax∣∣=12√3g2R
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage
33 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
A solid sphere of mass M and Radius R is attached to a massless spring of force constant k as shown in the figure. The cylinder is pulled towards right slightly and released so that it executes simple harmonic motion of time period. If the cylinder rolls on the horizontal surface without slipping, calculate its time period of oscillation.

View SolutionA cylindrical plastic bottle of negligible mass is filled with 310 ml of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic montion angular frequency ω. If the radius of the bottle is 2.5 cm then ω is close to: (density of water =103kg/m3)
View Solution
Knowledge Check
A solid sphere of density σ with one -third of tis volume submerged . When the sphere is pressed down slightly and released , it executes S.H.M of time period T. Then (viscous effect is ignored)
Ap=σ3Bp=3σC4π3√RgD3π2√RgA pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
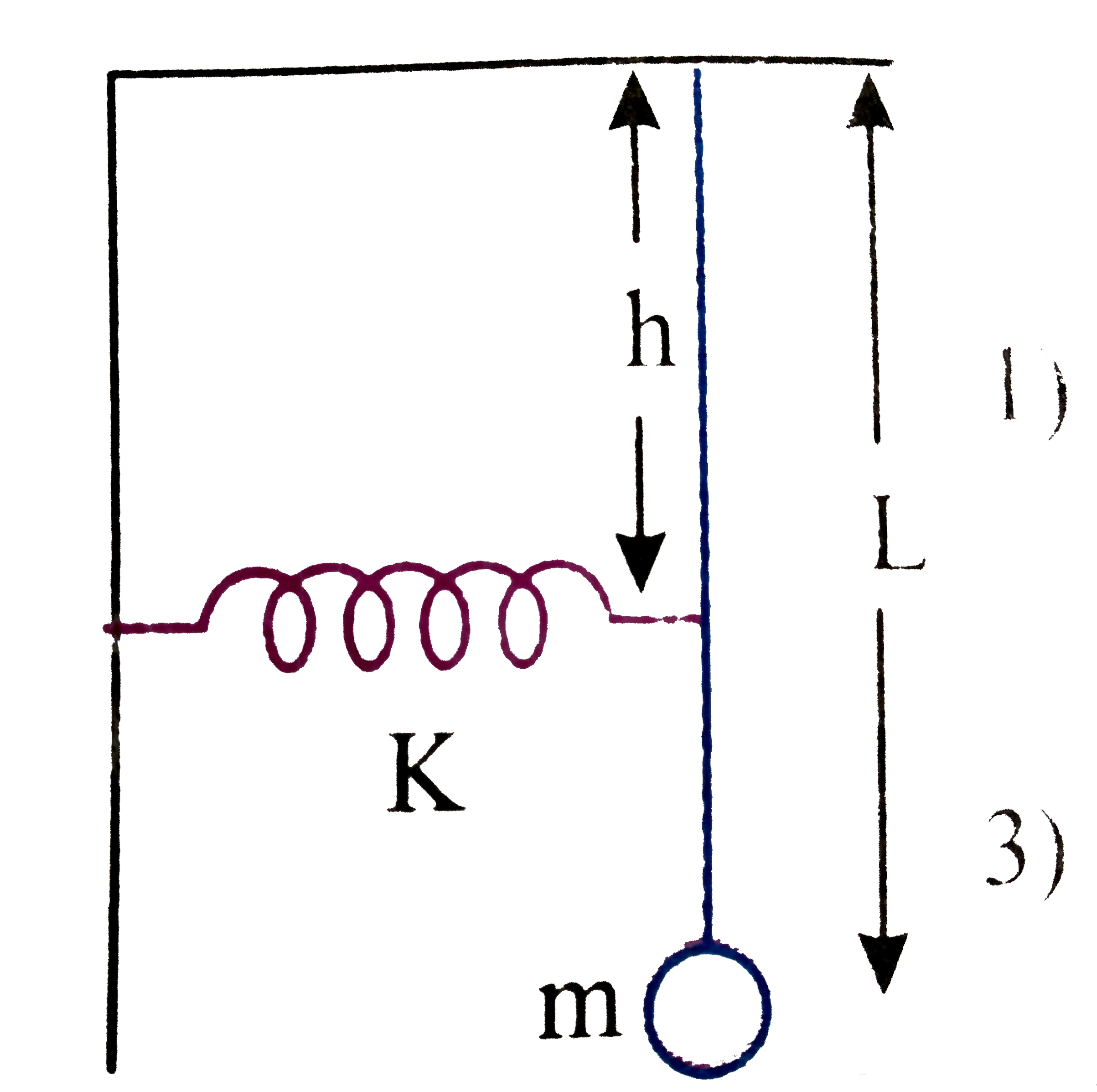 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2A uniform solid bar of wood floats vertically in water with 10 cm of its height immersed in the water. When it is slightly depressed and released, it oscillates with a frequency of
Aπ7HzB√2π7HzC7πHzD7√2πHz
A wooden cube (density of wood ρ3 ') of side l 'floats in a liquid of density ' ρ with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs simple harmonic motion of period T. Then, T is equal to 2π√xlyg. Find (x+y).
View SolutionFigure shown a container having liquid of variable density. The density of liquid veriesas ρ=ρ0(4−3hh0). Here, h0 and ρ0 are constants and h is measured from bottom of the container. A solid block of small dimensions whose density is 52ρ0 and mass m is released from bottom of the tank. Prove that the block will execute simple harmonic motion. Find the frequency of oscillation.
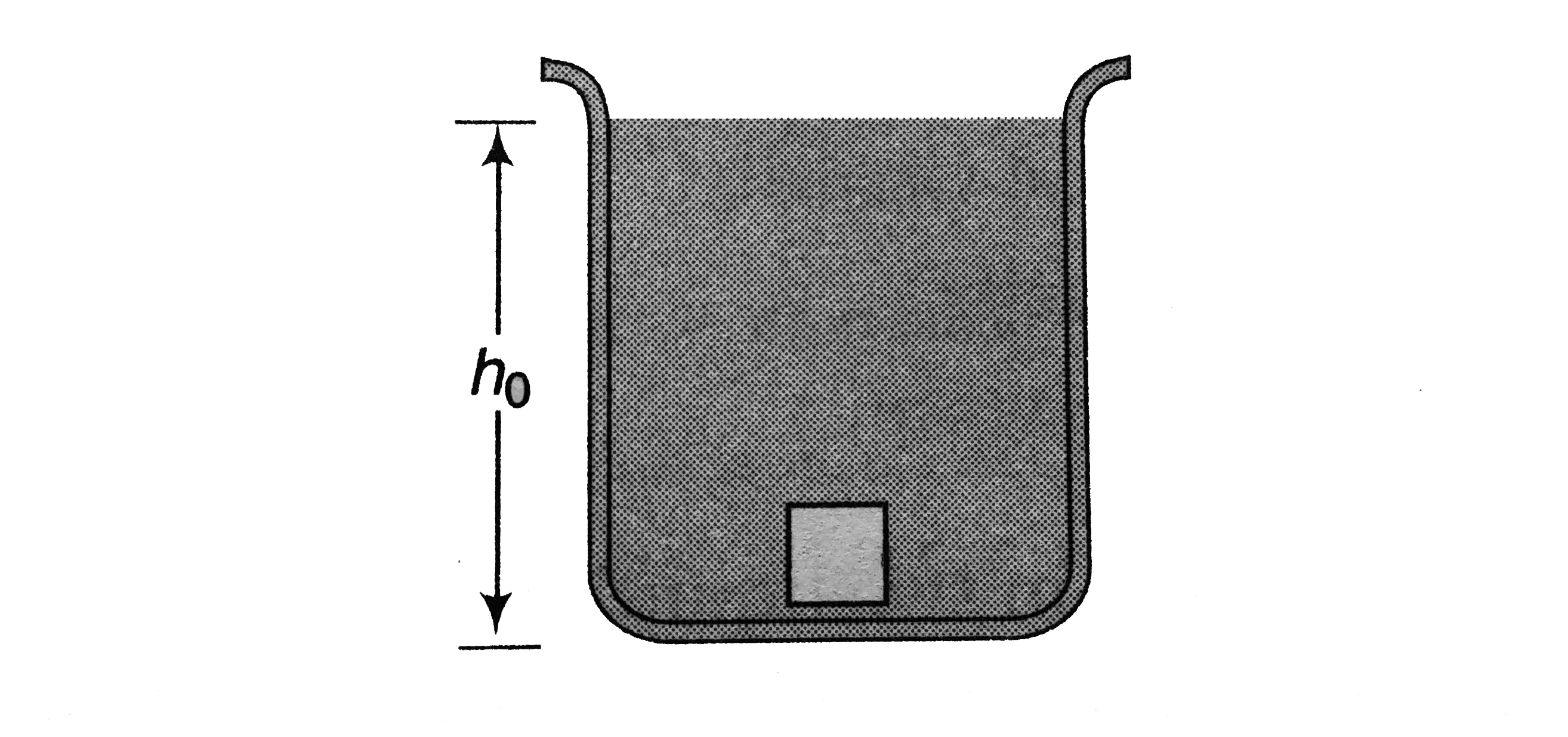 .
.
View SolutionA wooden cube (density of wood 'd') of side 'l' flotes in a liquid of density 'ρ' with its upper and lower surfaces horizonta. If the cube is pushed slightly down and released, it performs simple harmonic motion of period 'T'. Then, 'T' is equal to :-
View SolutionA wooden cylinder of length L is partly submerged in a liquid of specific gravity ρ1 with nth (n<1) part of it inside the liquid. Another immiscible liquid of density ρ2 is poured to completely submerge the cylinder. Density of cylinder ρ is the geometric mean of the densities of the two liquid.
When the cylinder is slightly depressed and released, it oscillates. let there be a mean position. find the time period of small oscillations below thee mean position
View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View Solution
