A wooden cube (density of wood 'd') of side 'l' flotes in a liquid of density 'ρ' with its upper and lower surfaces horizonta. If the cube is pushed slightly down and released, it performs simple harmonic motion of period 'T'. Then, 'T' is equal to :-
2π√lρ(ρ−d)g
2π√ldρg
2π√lρdg
2π√ld(ρ−d)g
The correct Answer is:B
To find the period T of the simple harmonic motion of a wooden cube floating in a liquid, we can follow these steps:
Step 1: Identify the mass of the cube
The mass m of the wooden cube can be calculated using the formula:
m=Volume×Density
The volume V of the cube with side length l is:
V=l3
Thus, the mass m of the cube is:
m=l3⋅d
where d is the density of the wood.
Step 2: Determine the area of the cube's base
The area A of the base of the cube is given by:
A=l2
Step 3: Calculate the restoring force
When the cube is pushed down slightly, the weight of the displaced liquid creates a restoring force. The volume of the submerged part of the cube when pushed down by a small distance x is:
Volume submerged=A⋅x=l2⋅x
The weight of the displaced liquid is:
Weight of displaced liquid=Volume submerged×Density of liquid×g=l2⋅x⋅ρ⋅g
The restoring force F acting on the cube is equal to the weight of the displaced liquid:
F=l2⋅x⋅ρ⋅g
Step 4: Relate the restoring force to acceleration
According to Hooke's law, the restoring force is also related to the acceleration a of the cube:
F=−kx
where k is the spring constant. The acceleration a can be expressed as:
a=Fm
Substituting the expression for F:
a=l2⋅x⋅ρ⋅gl3⋅d=l2⋅ρ⋅gl3⋅d⋅x=ρ⋅gl⋅d⋅x
Step 5: Find the period of simple harmonic motion
The period T of simple harmonic motion is given by:
T=2π√mk
From our previous steps, we have:
k=ρ⋅gl⋅d
Thus, substituting for m and k:
T=2π√l3⋅dl2⋅ρ⋅g=2π√l⋅dρ⋅g
Final Result
The period T of the simple harmonic motion is:
T=2π√l⋅dρ⋅g
The mass m of the wooden cube can be calculated using the formula:
m=Volume×Density
The volume V of the cube with side length l is:
V=l3
Thus, the mass m of the cube is:
m=l3⋅d
where d is the density of the wood.
The area A of the base of the cube is given by:
A=l2
When the cube is pushed down slightly, the weight of the displaced liquid creates a restoring force. The volume of the submerged part of the cube when pushed down by a small distance x is:
Volume submerged=A⋅x=l2⋅x
The weight of the displaced liquid is:
Weight of displaced liquid=Volume submerged×Density of liquid×g=l2⋅x⋅ρ⋅g
The restoring force F acting on the cube is equal to the weight of the displaced liquid:
F=l2⋅x⋅ρ⋅g
According to Hooke's law, the restoring force is also related to the acceleration a of the cube:
F=−kx
where k is the spring constant. The acceleration a can be expressed as:
a=Fm
Substituting the expression for F:
a=l2⋅x⋅ρ⋅gl3⋅d=l2⋅ρ⋅gl3⋅d⋅x=ρ⋅gl⋅d⋅x
The period T of simple harmonic motion is given by:
T=2π√mk
From our previous steps, we have:
k=ρ⋅gl⋅d
Thus, substituting for m and k:
T=2π√l3⋅dl2⋅ρ⋅g=2π√l⋅dρ⋅g
The period T of the simple harmonic motion is:
T=2π√l⋅dρ⋅g
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]
12 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MCQ s one or more than one correct answers
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A wooden cube (density of wood ρ3 ') of side l 'floats in a liquid of density ' ρ with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs simple harmonic motion of period T. Then, T is equal to 2π√xlyg. Find (x+y).
View SolutionA solid sphere of radius R is floating in a liquid of density σ with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
View Solution
Knowledge Check
A solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
A2π√ρ0ρagB2π√ρρ0agC2π ⎷a(1−ρρ0)gD2π ⎷a(1+ρρ0)gA pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
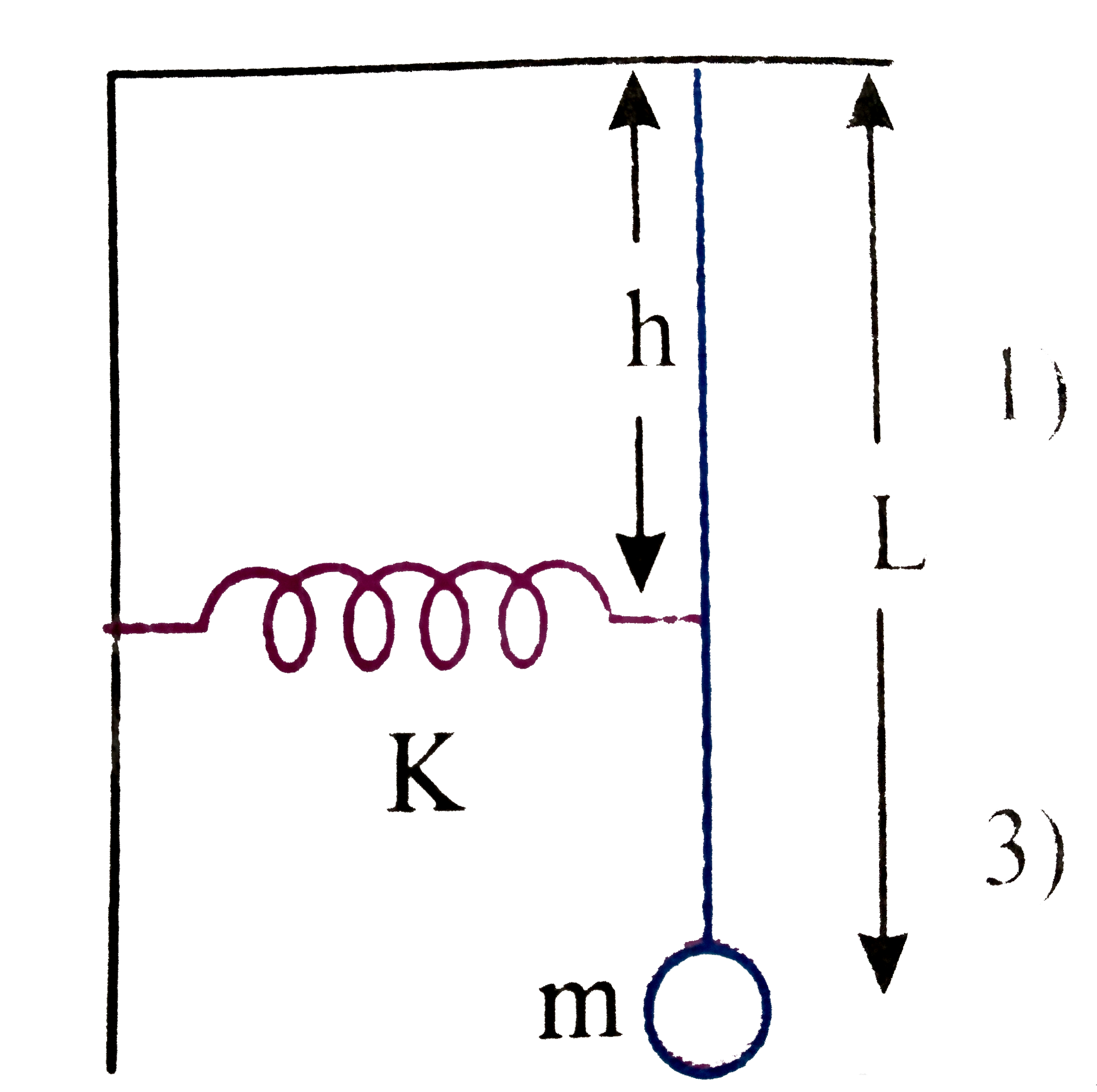 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2A solid sphere of density σ with one -third of tis volume submerged . When the sphere is pressed down slightly and released , it executes S.H.M of time period T. Then (viscous effect is ignored)
Ap=σ3Bp=3σC4π3√RgD3π2√Rg
A vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.
View Solution15.A small circular loop of conducting wire has radius a and carries current I. It is placed in a uniform magnetic field B perpendicular to its plane such that when rotated slightly about its diameter and released it starts performing simple harmonic motion of time period T.If the mass of the loop is m then:
View SolutionA cylidrical wooden piece of cork floats in a liquid of density σ. The cork is depressed slightly and released. Show that the cork will oscillate up and down simple harmonicaly with a period.
T=2π√ρhσg, where ρ is the density of the cork.
View SolutionA particle of mass 1 kg is hanging from a spring of force constant 100 Nm1 . The mass is pulled slightly downward and released so that it executes free simple harmonic motion with time period T. The time when the kinetic energy and potential energy of the system will become equal, is Tx The value of x is_______
View SolutionA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
View Solution
