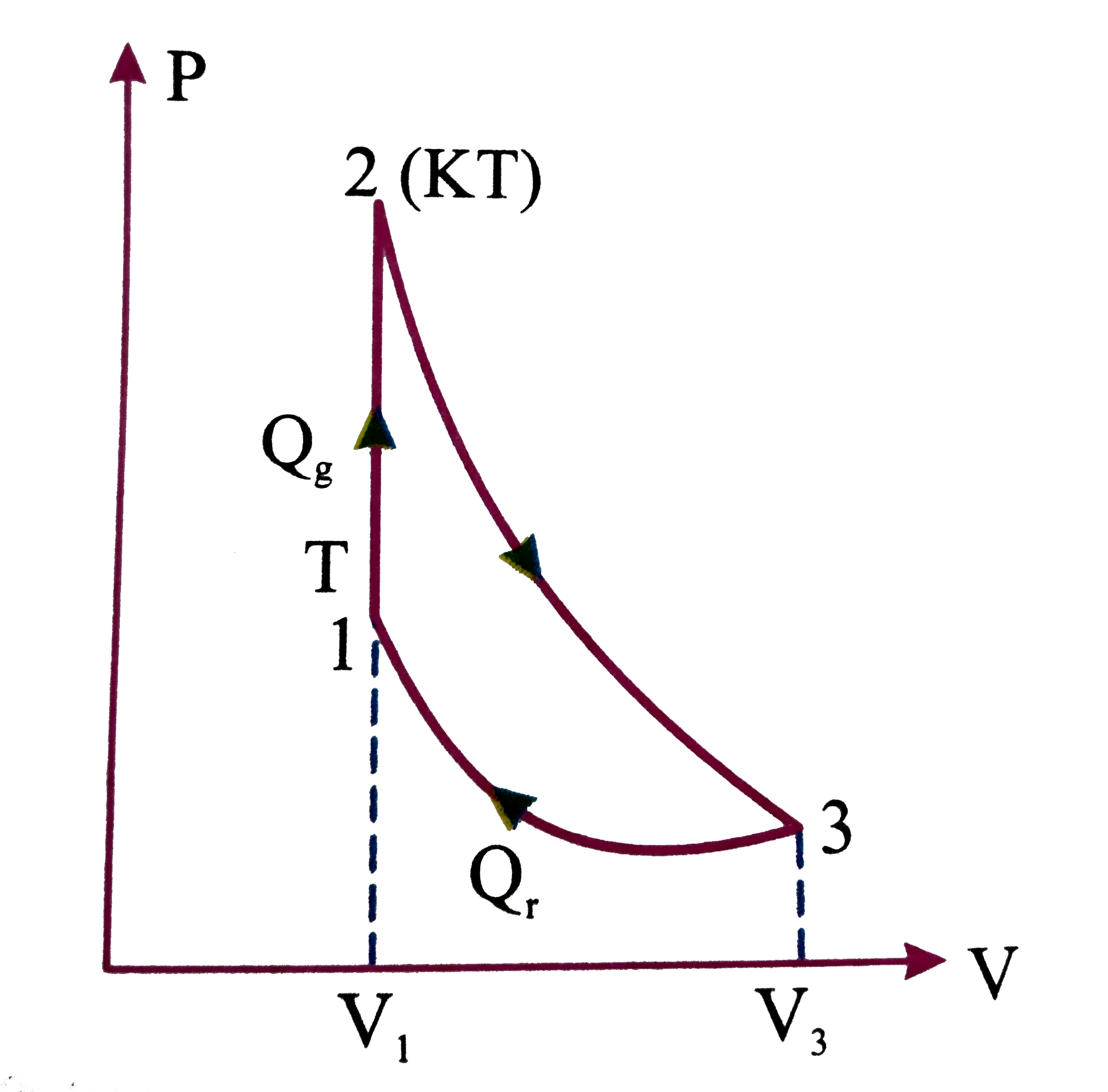
An ideal gas goes through a cycle consisting of ischoric adiabatic and isothermal lines. The isothermal process is perform at minimum temperature. If the absolute temperature varies K times with tn the cycle then find out its effcincy.
1−lnKl
1+lnKl
lnKl
llnK
The correct Answer is:A
Process 2→3 is adiabatic expansion and 3→1 is isothermal compression.
From process 2→3 , the internal energy continuosly decrease (I.e., temperature continuously decrease) Point 2 is at highest temerature
Qg=Ncv(KT−T), Qr=nRTInV3V1
Process
2→3(KT)Vγ−11=TVγ−13⇒V3V1=(K)1/(γ−1)
η=Qg−QrQ8=1−QrQg=1−InKl
Topper's Solved these Questions
Similar Questions
An ideal gas goes through a cycle consisting of
(a) isochoric, adiabatic, and isothermal lines ,
(b) isobaric, adiabatic, and isothermal lines,
with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the absolute temperature varies n−fold within the cycle.
View SolutionAn ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies n−fold within the cycle.
View Solution
Knowledge Check
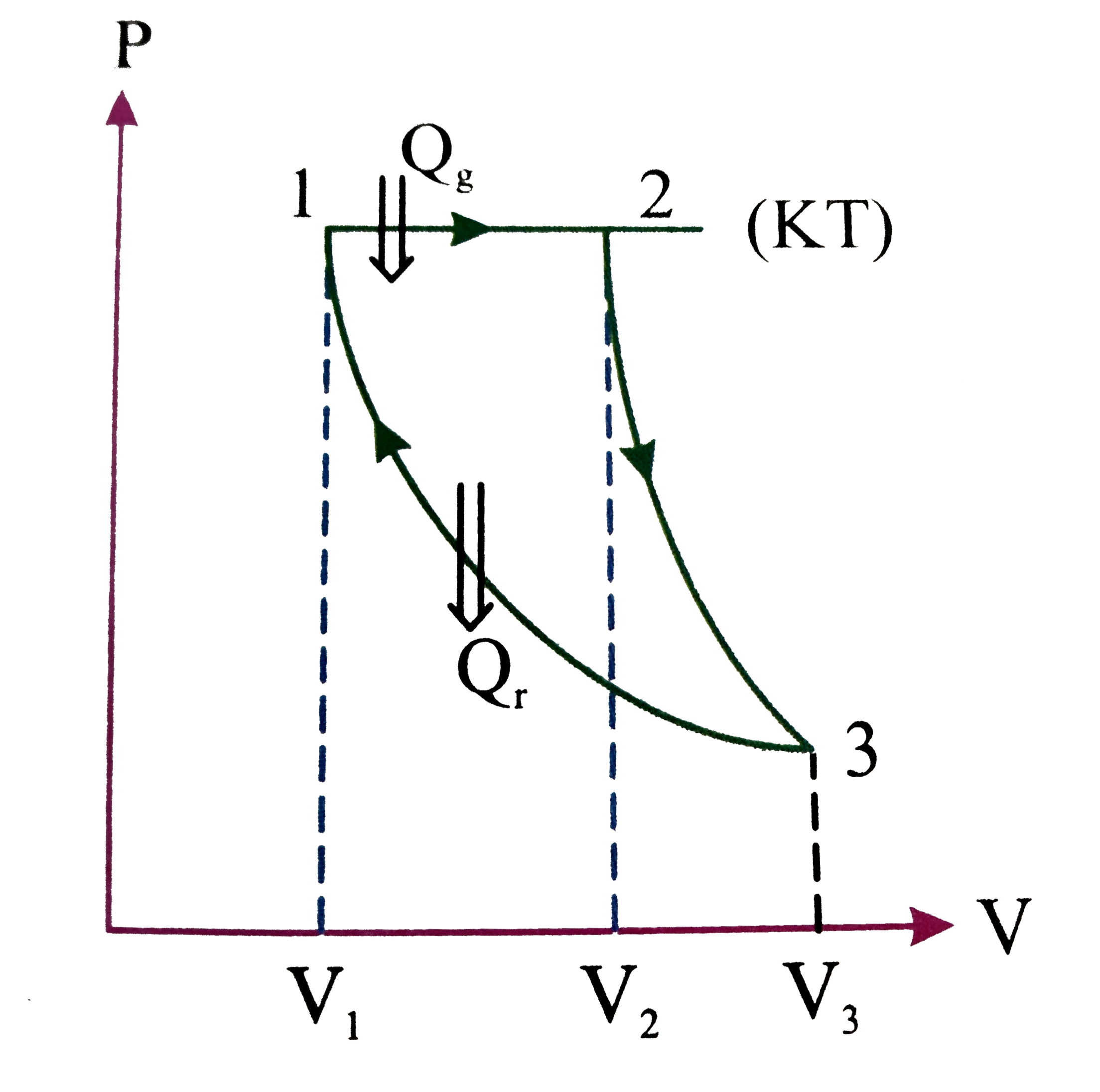
A cycle is made of three process is iso barie, adiabatic and isothermal. Isothermal process has minimum temperature. Absolute temperature charges by k times withing the cycle. Find out the efficiency.
 A1−1nK(K−1)B1+1nK(K−1)C1+1nK(K+1)Dnone of these
A1−1nK(K−1)B1+1nK(K−1)C1+1nK(K+1)Dnone of theseAn ideal gas undergoes a process consisting of adiabatic and isothermal process only as shown in the figure. Then :
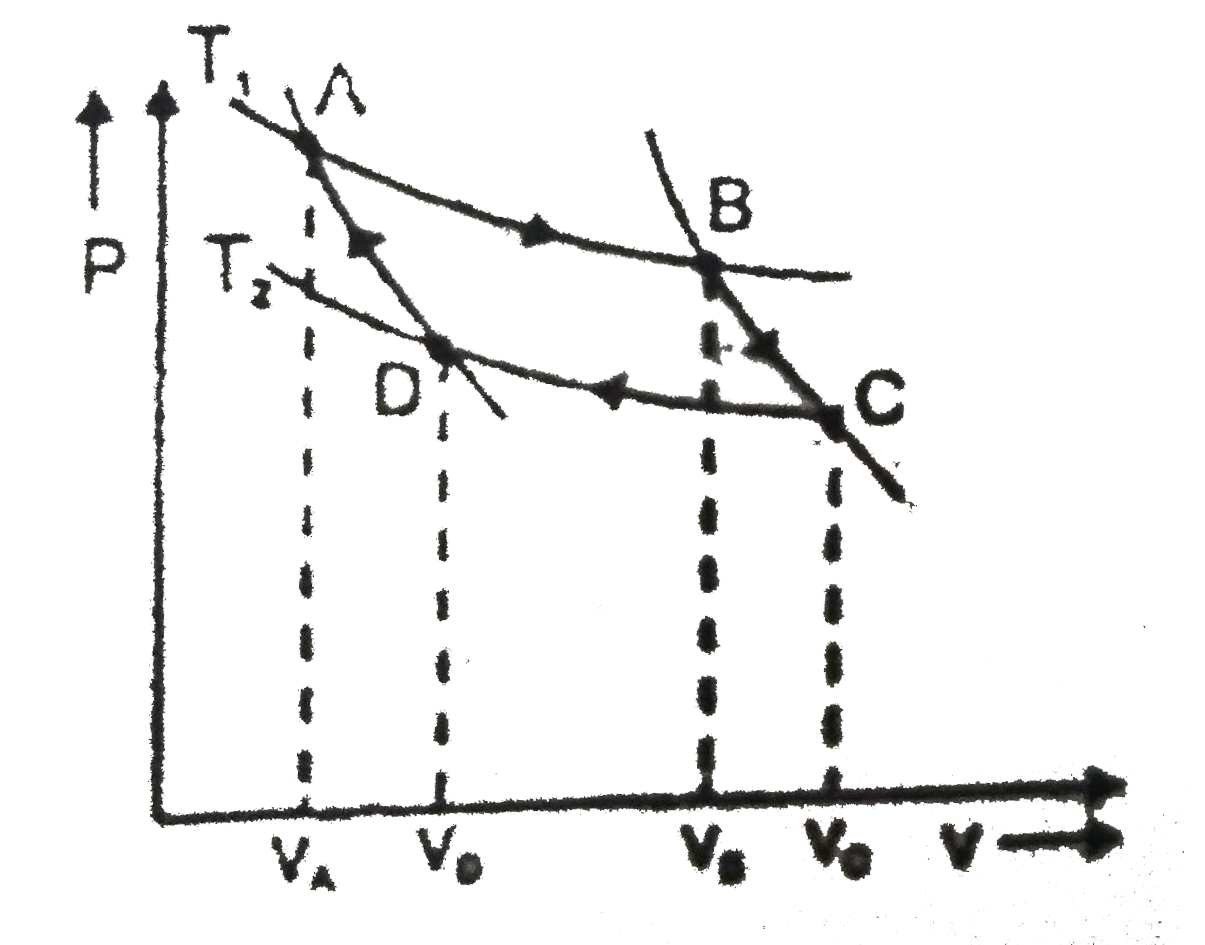 AT1<T2BVAVC=VBVDCwork done by the gas in process will be negativeDefficiency =WAB+WBCQAB
AT1<T2BVAVC=VBVDCwork done by the gas in process will be negativeDefficiency =WAB+WBCQABHelium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)
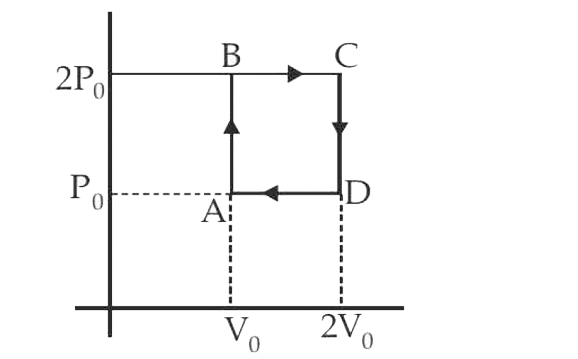 A15.4%B9.1%C10.5%D12.5%
A15.4%B9.1%C10.5%D12.5%
An ideal gas whose adiabatic exponent equals γ goes through a cycle consisting of two isochoric and two isobaric lines. Find the efficiency of such a cycle, if the absolute temperature of the gas rises n times both in a isochoric heating and in the isobaric expansion.
View SolutionAn ideal gas goes through a cycle consisting of alternate isothermal and adiabatic curves (Fig. 2.2). The isothermal processes proceed at the temperatures T1,T2 and T3. Find the efficiency of such a cycle, if in each isothermal expansion the gas volume increases in the same alphaortion.
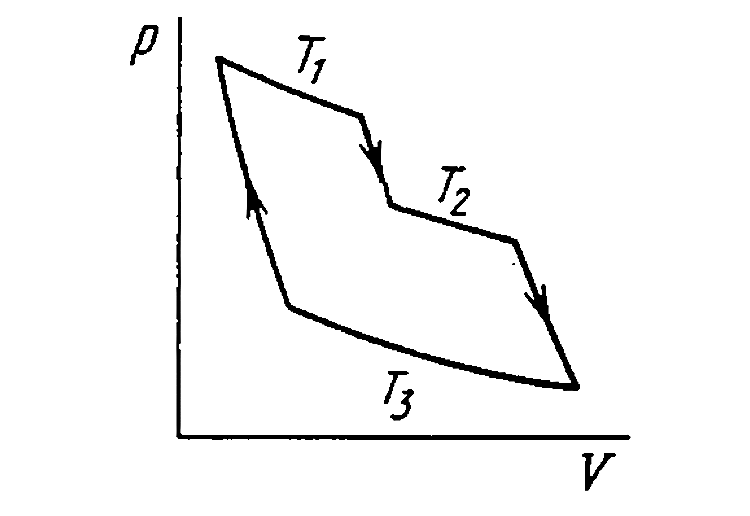 .
.
View SolutionFind the efficiency of a cycle consisting of two isobaric and two isothermal lines if the pressure varies n−fold and the absolute temperature τ−fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
View SolutionAn ideal monoatomic gas (γ=53) goes through a cyclic process consisting two isochoric and two isobaric lines. The absolute temperature of the gas rises two times both in isochoric heating and isobaric expansion. If number of moles are three, find efficiency of cyclic process.
View SolutionFind the efficiency of a cycle consisting of two isochoric and two isothermal lines if the volume varies v−fold and the absolute temperature τ−fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
View Solution
