5 moles of nitrogen gas are enclosed in an adiabatic cylindrical vessel. Thel piston itself is a rigid light cylindrical container containing 3 moles of helium gas. There is a heater which given out a power of 30 cal is transferred to helium through the batton surface of the piston. The rate of incremnt of temperature of the nitrogen gas assuming that the piston
moves slowly, is 
2K/s
4K/s
6K/s
8K/s
The correct Answer is:A
Net power given to N2 gas =100−30=70 cal/s
The nitrogen gas expands isobarically
∴Q=nCpdTdtor70=5×72RdTdt
∴dTdt=2K/s
Topper's Solved these Questions
Similar Questions
A rigid container of negligible heat capacity contains one mole of an ideal gas. The temperatures of the gas increases by 1∘C if 3.0 cal of heat is added to it. The gas may be
View Solution2 moles of a diatomic gas are enclosed in a cylinder piston arrangment. The area of cross section and mass of the piston are 1cm2 and 1 kg respectively. A heater is supplying heat to the gas very slowly. Find heat supplied (in joule) by the heater is the piston moves through a distance of 10 cm.
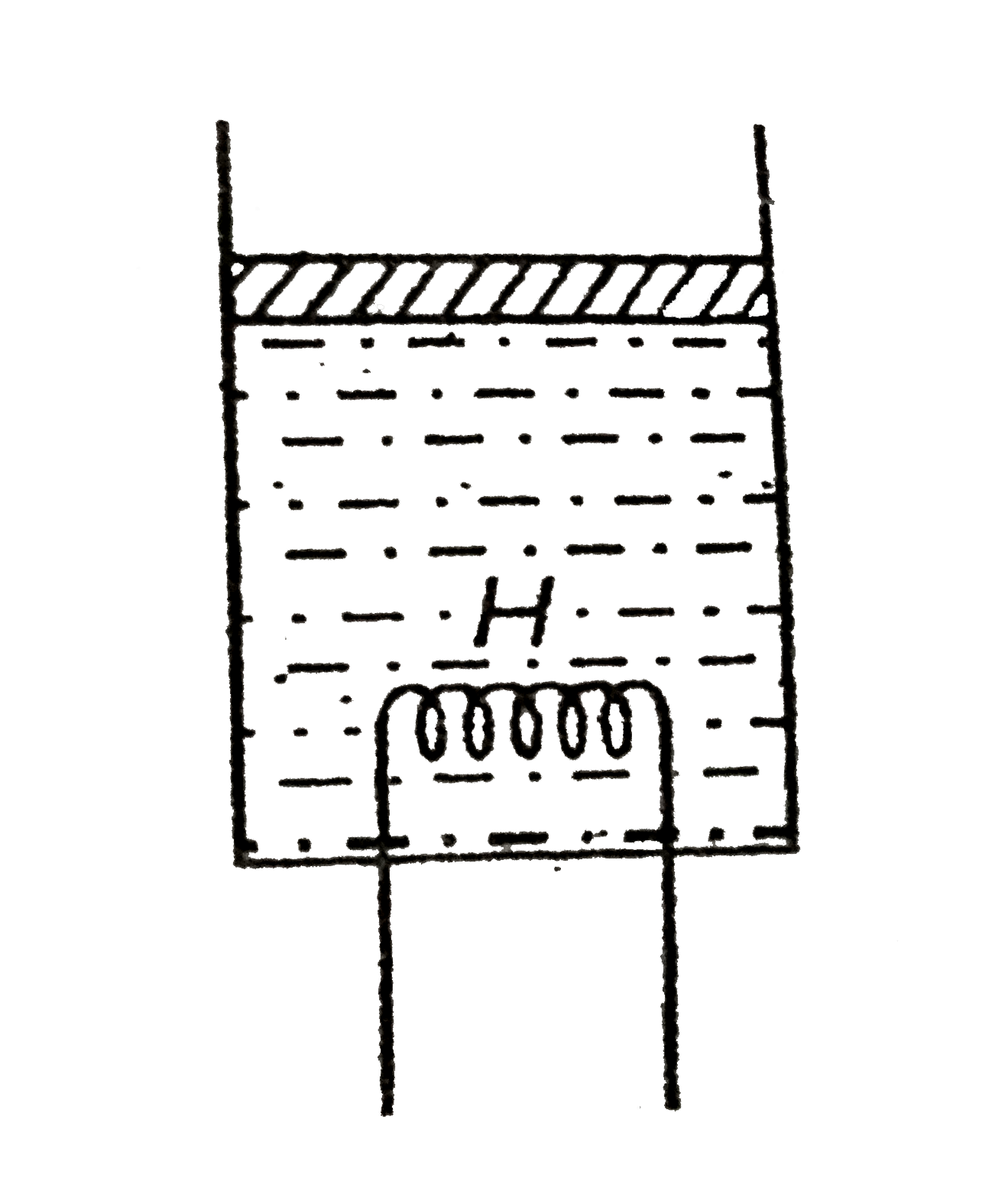.View Solution
Knowledge Check
- Question 1 - Select One
A vertical cylinder with heat - conducting walls is closed at the bottom and is fitted with a smooth light piston. It contains one mole of an ideal gas. The temperature of the gas is always equal to the surrounding 's temperature, T0 The piston is moved up slowly to increase the volume of the gas to η times. Which of the following is incorrect?
AWork done by the gas is RT0 In η.BWork done against the atmosphere is RT0(η−1).CThere is no change in the internal energy of the gas.DThe final pressure of the gas is 1η−1 times its initial pressure. - Question 2 - Select One
A resistance coil, connected to an external battery is placed inside an adiabatic cylinder filled with frictionless piston of mass m and containing an ideal gas. A current i flows through the coil, which has resistance R. The speed with which the piston must move in order to keep the temperature of the gas constant will be
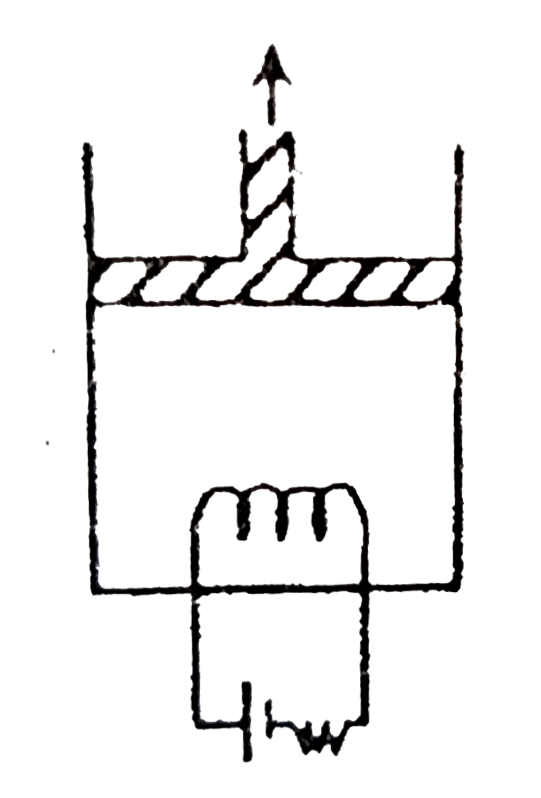Ai2R/mgBiR/mgC0DData is insufficient. - Question 3 - Select One
An ideal gas is enclosed in a vertical cylindrical container and supports a freely moving piston of mass M. The piston and the cylinder have an equal cross-sectional area A. Atmospheric pressure is p0 and when the piston is in equilibrium, the volume of the gas is V0. The piston is now displaced slightly from its equilibrium position. Assuming that the system, is completely isolated from, its surroundings, what is the frequency of oscillation.
Af=12π√γ(p0A2+MgA)V0MBf=12π√1γ(p0A2+MgA)V0MCf=12π√(p0A2+MgA)V0MDf=12π√A(p0A2+MgA)V0M
An adiabatic cylindrical chamber with a frictionless movable piston has been placed on a smooth horizontal surface as shown. One mole an ideal monotonic gas is enclosed inside the chamber. Mass of the piston is M and mass of the remaining chamber including the gas is 4 M. The gas is at atmospheric pressure and temperature. A particle of mass M moving horizontally with speed v, strikes the piston elastically. Find the change in temperature of the gas when the compression is maximum.
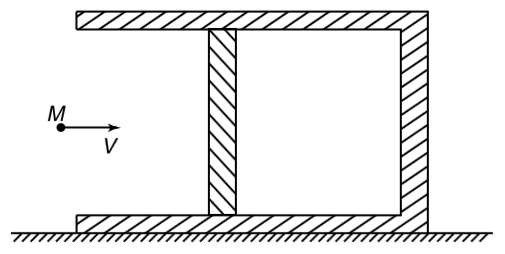
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View Solution(i) A conducting piston divides a closed thermally insulated cylinder into two equal parts. The piston can slide inside the cylinder without friction. The two parts of the cylinder contain equal number of moles of an ideal gas at temperature T0. An external agent slowly moves the piston so as to increase the volume of one part and decrease that of the other. Write the gas temperature as a function of ratio (β) of the volumes of the larger and the smaller parts. The adiabatic exponent of the gas is γ.
(ii) In a closed container of volume V there is a mixture of oxygen and helium gases. The total mass of gas in the container is m gram. When Q amount of heat is added to the gas mixture its temperature rises by ΔT. Calculate change in pressure of the gas.View SolutionAn amount n (in moles) of a monatomic gas at initial temperature T0 is enclosed in a cylinderical vessel fitted with a ligth piston. The surrounding air has a temperature Ts(>T0) . And the atmospheric pressure is Pa . Heat may be conducted between the surrounding and the gas through the bottom of the cylinder. The bottom has a surface area A, thickness x and thermal conductivity K. Assuming all change to be slow, find the distance moved by the piston in time t.
View SolutionTwo moles of a diatomic gas at 300K are enclosed in a cylinder as shown in figure. Piston is light. Find out the heat given if the gas is slowly heated to 400K in the following three cases.
(i) Piston to free to move
(ii) If piston does not move
(iii) If piston is heavy and movable
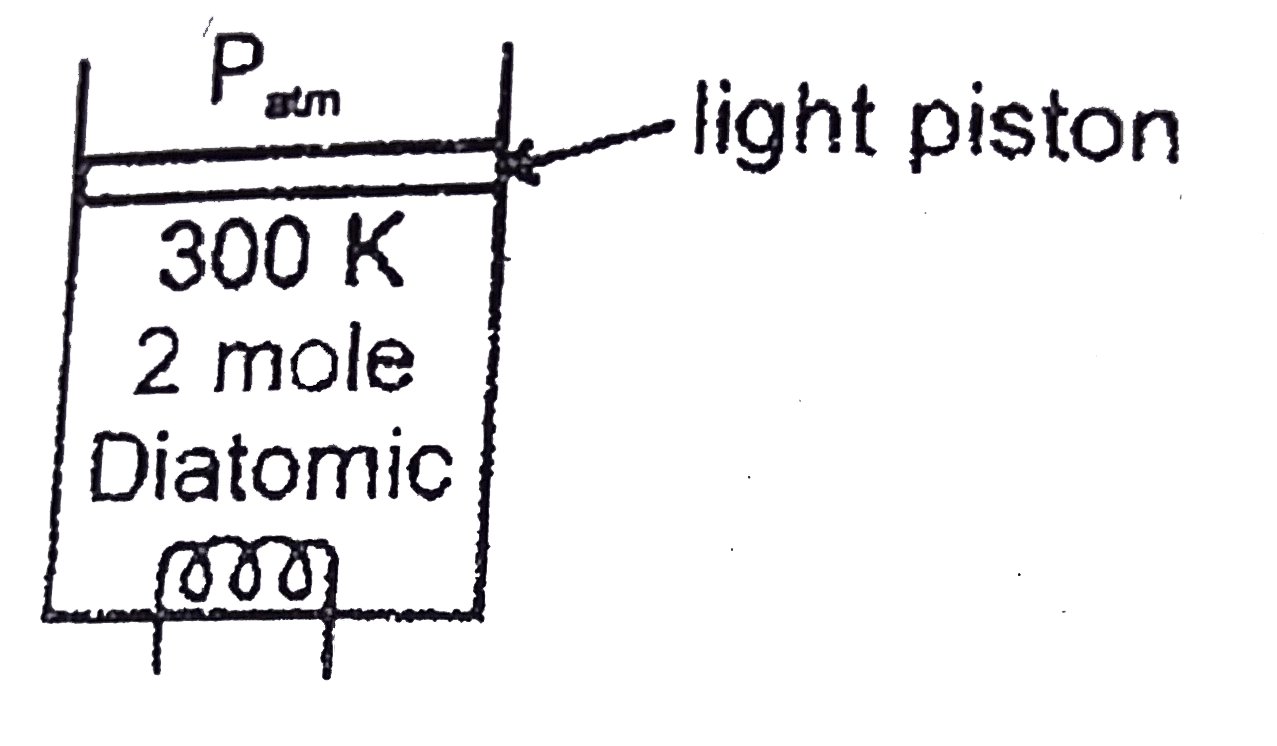
View Solution