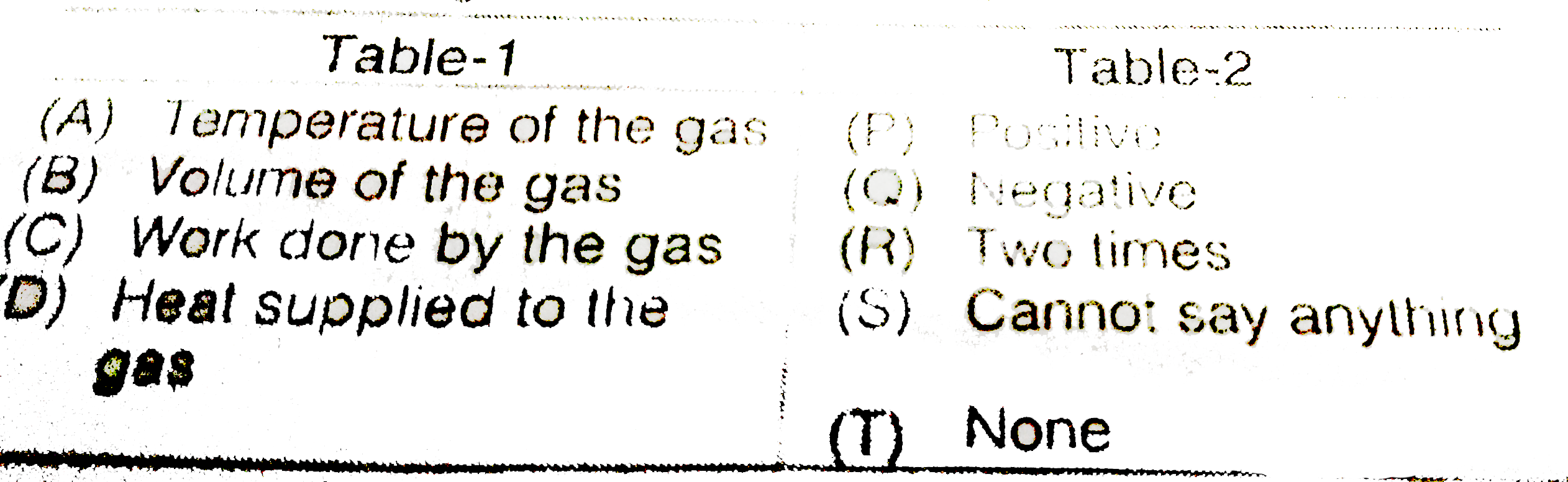An ideal monoatomic gas indergoes a pressure pVn=constant. The adiabatic constant for gas is y. During the process, volume of gas increases from V0 to rV0 and pressure decreases for p0 to p02r Based on above information, answer the following questios :
The molar heat capacity of the gas for the process is
R(n−γ)(n−1)(γ−1)
R(n−1)(n−γ)(γ−1)
Rγ−1
Rn−1+Rγ
The correct Answer is:A
C=Cv+R1−n
=Rγ−1−Rn−1=R(n−γ)(γ−1)(n−1)
Topper's Solved these Questions
Similar Questions
Knowledge Check
An ideal monoatomic gas indergoes a pressure pVn=constant. The adiabatic constant for gas is y. During the process, volume of gas increases from V0 to rV0 and pressure decreases for p0 to p02r Based on above information, answer the following questios :
The of n isA2logrlog2rBlog2r3Clog2rlogrDlog2r3logrOne mole of an ideal monoatomic gas undergoes a described by the equations PV3= constant The heat the gas during this process is :
A2RBRC32RD53RFor a certain process pressure of diatomic gas varies according to the relation P=aV2n, where a is constant. What is the molar heat capacity of the gas for this process?
A17R6B6R17C13R6D16R7
An ideal diatomic gas undergoes a process in which the pressure is proportional to the volume. Calculate the molar specific heat capacity of the gas for the process.
View SolutionAn ideal gas expands in such a manner that its pressure and volume can be related by equation PV3=constant. During this process, the gas is
View SolutionFor a certain process, pressure of diatomic gas varies according to the relation P=aV2, where a is constant. What is the molar heat capacity of the gas for this process ?
View SolutionAn ideal gas expands in such a manner that its pressure and volume can be related by equation PV2= constant. During this process, the gas is
View SolutionOne mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
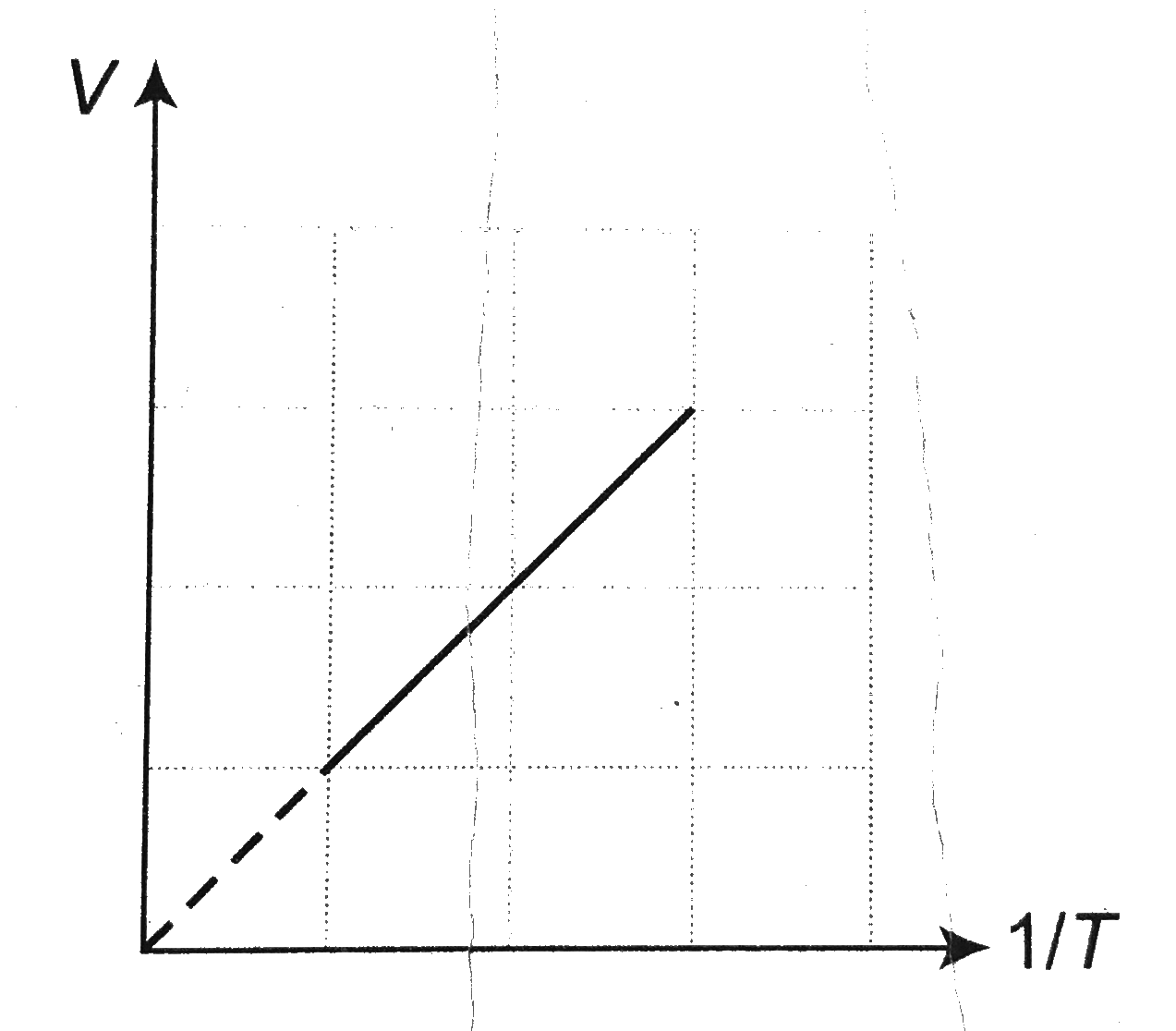
R is a gas constant.
View Solution