In Fig., a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulating material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. the lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. the heat capacities per mole of an ideal monoatomic gas are Cυ=32RandCP=52R, and those for an ideal diatomic gas are Cυe=52RandCP=72R.
Consider the partition to be rigidly fixed so that it does not move. when equilibrium is achieved, the final temperature of the gases will be

550K
525K
513K
490K
The correct Answer is:D
Let final temperature of both comparments is T . Heat given by lower compartment
Q=nCpΔT=2×52R×(700−T) ….(i)
Heat obtained by upper compartment
Q=nCpΔT=2×72R×(T−400)
By equatin (i) and (ii)
5(700−T)−7(T−400)
3000−5T=7T−2800
6300−12T
T=525K
Work done by lower gas
WL=PΔV=nRΔT=−350R
Work done by upper gas
Wu=PΔV=nRΔT=+250R
Net work done
WL+WU=−350+250=−100R
Topper's Solved these Questions
Similar Questions
The ratio of coefficients of apparent expansions of the same liquid in two different vessels is 1:2. If α1 and α2 are the coefficient of linear expansions then coefficient of real expansion of the liquid is
View SolutionThree metal rods of coefficient of thermal conductivities K,2K,3K conducts heats of 3Q,2Q,Q per seconds through unit area then the ratio of temperature gradients .
View SolutionIn the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monatomic gas at 700K and the upper compartment is filled with 2 moles of an ideal diatmoic gas at 400K. The heat capacities per mole of an ideal monatomic gas are CV=32R,CP=52R, and those for an ideal diatomic gas are CV=52R,CP=72R,

Consider the partition to be rigidly fixed so that it does not move. When equilibrium is achieved, the final temperature of the gasses will be
View SolutionIn the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monatomic gas at 700K and the upper compartment is filled with 2 moles of an ideal diatmoic gas at 400K. The heat capacities per mole of an ideal monatomic gas are CV=32R,CP=52R, and those for an ideal diatomic gas are CV=52R,CP=72R,

Now consider the partition to be free to move without friction so that the pressure of gasses in both compartments is the same. The total work done by the gases till the time they achives equilibrium will be
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate The final presssures of left and right compartment respectively are
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of the left compartment.
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of right compartment.
View SolutionIn Fig., a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulating material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. the lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. the heat capacities per mole of an ideal monoatomic gas are Cυ=32RandCP=52R, and those for an ideal diatomic gas are Cυe=52RandCP=72R.
Consider the partition to be rigidly fixed so that it does not move. when equilibrium is achieved, the final temperature of the gases will be

View SolutionIn Fig., a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulating material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. the lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. the heat capacities per mole of an ideal monoatomic gas are Cυ=32RandCP=52R, and those for an ideal diatomic gas are Cυe=52RandCP=72R.
Now consider the partition to be free to move without friction so that the pressure of gases in both compartments is the same. the total work done by the gases till the time they achieve equilibrium will be

View SolutionA diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.
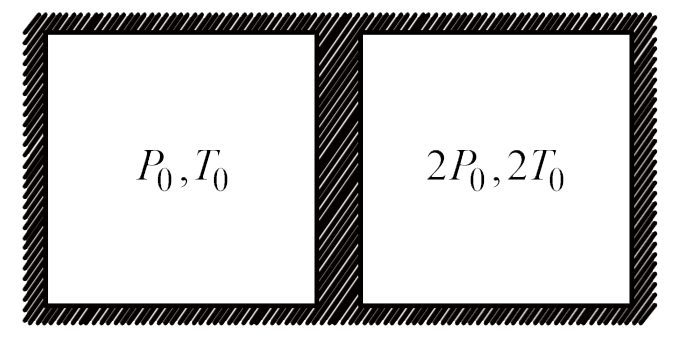
If the pin which was keeping the piston fixed is removed and the piston is allowed to slide slowly such that a state of mechanical equilibrium is achieved. The volume of left compartment when piston is in equilibrium is
View SolutionA container has a tight fitting movable piston which can slide without friction. The compartment containing spring has vacuum and to the left of the piston there is diatomic gas. If vacuum is created in the right compartment also the piston touches the right wall and the spring is relaxed. Find the heat capacity of the system neglecting the heat capacities of the material of spring, container and the piston. Express your answer in terms of P_(0), V_(0) and T_(0) .
View SolutionA container of volume 1m3 is divided into two equal compartments by a partition. One of these compartments contains an ideal gas at 300 K . The other compartment is vacuum. The whole system is thermally isolated from its surroundings. The partition is removed and the gas expands to occupy the whole volume of the container. Its temperature now would be
View SolutionA partition divides a container having insulated walls into two compartments I and II . The same gas fills the two compartment. What is the ratio of the number of molecules in compartments I and II ?
View SolutionThe figure shows an insulated cylinder of volume V containing monoatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed, and the system is allowed to acquire a state of thermal equilibrium. If the initial pressures and temperatures are as shown.
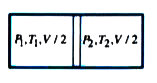
Calculate the final volume of gas in each compartment.
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate The final presssures of left and right compartment respectively are
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of the left compartment.
View Solution

