Figure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of the left compartment.
V2(P1T2P2T1+P1T2)
V(P1T2P2T1−P1T2)
V(P1T2P2T1+P1T2)
V(2P1T2P2T1+P1T2)
The correct Answer is:C
P'1=P1T2(P1+P2)(P1T2+P2T1) and P'2=P2T1(P1+P2)(P1T2+P2T1)
As P2T1>P1T2 (given)
Hence, P'2>P'1
Let ΔV be the change in volume of any compartments.
P((V/2)−ΔV)T=P1V2T1
P(V/2)+ΔVT=P2V2T2
Dividing, we get
((V/2)+ΔV)((V/2)−ΔV)=P2T1P1T2
ΔV=V2(P2T1−P1T2P2T1+P1T2)
Volume of left compartment
V'1=V2−ΔV=V(P1T2P2T1+P1T2)
Volume of right compartment
V'2=V2+ΔV=V(P2T1P2T1+P1T2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning6videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
Figure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final temperatureView SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final presssures of left and right compartment respectively areView SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The heat that flows from RHS to LHS, Given T2>T1.
Now, the pin which was keeping the piston fixed is removed. and the piston is set free to move. The piston is allowed to slide slowly, such that of mechanical equilibrium is also achieved and T1P2>P1T2. Find.View SolutionFigure shows an adiabatic cylindrical tube of volume (V0) divided in two parts by a frictionless adiabatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (P1) and the temperatures (T1) is injected into the left part and the another ideal gas at pressures (P2) and temperature (T2) is injected into the right part. (CpCv=γ) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find
(a) the volumes of the parts,
(b) the heat given to the gas in the left part and
(c) the final common pressure of the gases.
 View Solution
View SolutionA vertical thermally insulated cylinder of volume V contain n moles of an ideal monoatomic gas under a weightless piston. A load of weight W is placed on the piston as a result of which the piston is displaced. If the initial temp of the gas is 300K, area of piston is A and atmospheric pressure P0. (take W=P0A). Determine the value of final temperature of the gas
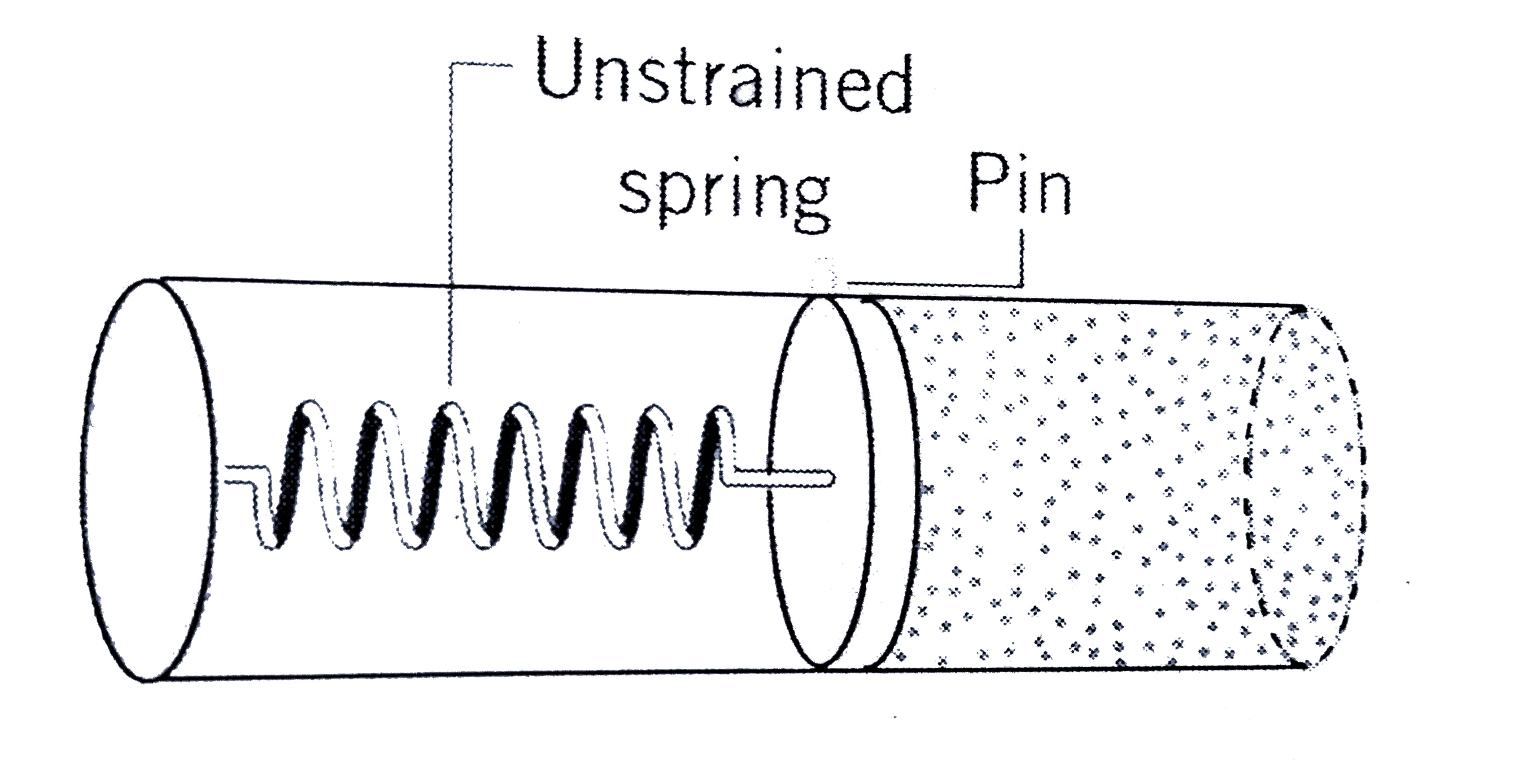
View SolutionA gas fills the right portion of a horizontal cylinder whose radius is 5.00cm. The initial pressure of the gas is 101kPa. A frictionless movable piston separates the gas from the left portion of the cylinder, which is evacuated and contains an ideal spring, as the drawing shows. The piston is initially unstrained, and the length of the gas-filled portion is 20.0cm. Wheen the pin is removed and the gas is allowed to expand, the length of the gas-filled chamber doubles when it finally reaches equilibrium. The initial and final temperatures are equal. Determine the spring constant of the spring.
 View Solution
View SolutionTen moles of a diatomic perfect gas are allowed to expand at constant pressure. The initial volume and temperature are V0 and T0 respectively. If 72RT0 heat is transferred to the gas, then the final volume and temperature are
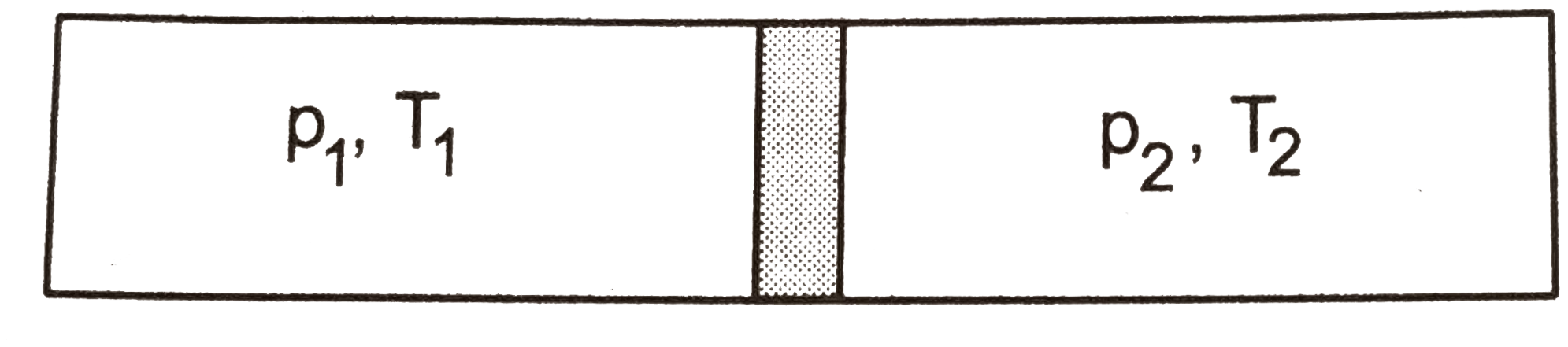
View SolutionFig shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1,T1 on the left and p2,T2 on the right. the system is left for sufficient time so that the temperature becomes equal on the two sides. (a) how much work has been done by the gas on the left part ? (b) find the final pressures on the two sides. (c ) find the final equilibrium temperature. (d) how much heat has flown from the gas on the right to the gas on the left ?
 View Solution
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
View Solutionn moles of a gas filled in a container temperature T is in thermodynamic equilibrium initially. If the gas is compressed slowly and isothermally to half its initial volume volume the work done by the atmosphere on the piston is :
 View Solution
View Solution
