Piston cylinder device initially contains 0.5m3 of nitrogen gas at 400kPa and 27∘C. An electric heater within the device is turned on and is allowed to apss a current of 2A for 5min from a 120V source. Nitrogen expands at constant pressure and a heat loss of 2800J occurs during the process.
R=25/3kJ/kmol−K
Number of moles of nitrogen gas is
0.8kmol
0.08kmol
0.8mol
0.08mol
The correct Answer is:B
To find the number of moles of nitrogen gas in the piston-cylinder device, we can use the ideal gas equation, which is given by:
PV=nRT
Where:
- P = Pressure (in Pa)
- V = Volume (in m³)
- n = Number of moles
- R = Ideal gas constant (in J/(kmol·K))
- T = Temperature (in K)
Step 1: Convert the given values to appropriate units
- Pressure P=400kPa=400×103Pa
- Volume V=0.5m3
- Temperature T=27∘C=27+273=300K
- The value of R=253kJ/(kmol⋅K)=25×1033J/(kmol⋅K)
Step 2: Substitute the values into the ideal gas equation
We can rearrange the ideal gas equation to solve for n:
n=PVRT
Substituting the values we have:
n=(400×103Pa)×(0.5m3)(25×1033J/(kmol⋅K))×(300K)
Step 3: Calculate the numerator
Calculating the numerator:
400×103×0.5=200000Pa⋅m3=200000J
Step 4: Calculate the denominator
Calculating the denominator:
R×T=(25×1033)×300=25×300×1033=7500×1033=2500×103J/kmol
Step 5: Calculate the number of moles
Now substituting back into the equation for n:
n=2000002500×103
Step 6: Simplify the fraction
n=2000002500000=225
Step 7: Convert to kilo moles
To convert to kilo moles:
n=225kmol=0.08kmol
Final Answer
Thus, the number of moles of nitrogen gas is:
n=0.08kmol
- P = Pressure (in Pa)
- V = Volume (in m³)
- n = Number of moles
- R = Ideal gas constant (in J/(kmol·K))
- T = Temperature (in K)
- Pressure P=400kPa=400×103Pa
- Volume V=0.5m3
- Temperature T=27∘C=27+273=300K
- The value of R=253kJ/(kmol⋅K)=25×1033J/(kmol⋅K)
We can rearrange the ideal gas equation to solve for n:
Calculating the numerator:
Calculating the denominator:
Now substituting back into the equation for n:
n=2000002500000=225
To convert to kilo moles:
Thus, the number of moles of nitrogen gas is:
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
Piston cylinder device initially contains 0.5m3 of nitrogen gas at 400kPa and 27∘C. An electric heater within the device is turned on and is allowed to apss a current of 2A for 5min from a 120V source. Nitrogen expands at constant pressure and a heat loss of 2800J occurs during the process.
R=25/3kJ/kmol−K
Electric work done on the nitrogen gas is
View SolutionA 2.5L flask contains 0.25mol each of sulphur dioxide and nitrogen gas at 27∘C. Calculate the partial pressure exerted by each gas and also the total pressure.
View Solution
Knowledge Check
The kinetic enerrgy of 4 mole sof nitrogen gas at 127∘C is (R=2 cal mol−1K−1)
A4400 calB3200 calC4800 calD1524 cal
The piston cylinder arrangement shown contains a diatomic gas at temperature 300 K The cross sectinal area of the cylinder is 1m2. Initially the height of the piston above th base of the cyclinder is 1 m. The temperature is now raised to 400 K at constant pressure. There is no heat loss in the process..
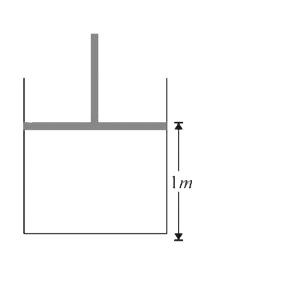
Find the new height (in m) of the piston above the base of the cylinder.
View SolutionTwo moles of an ideal gas are allowed to expand from a volume of 10dm3 to 2 m3 at 300 K against a pressure of 101.325 kPa. Calcualte the work done.
View SolutionAt 27∘C two moles of an ideal monatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate
(a) final temperature of the gas
(b) change in its internal energy and
(c) the work done by the gas during the process. [ R=8.31J/mol−K]
View SolutionCalculate the amount of heat that must be supplied to 40 gm of nitrogen to raise its temperature by 45∘C at constant pressure if it is at room temperature. R=8.3Jmol−1K−1.
View SolutionA cylinder contains hydrogen gas at pressure of 249kPa and temperature 27degreeC. Its density is (R=8.3Jmol−1K−1)
View SolutionOne moles of an ideal gas which CV=3/2R is heated at a constant pressure of 1atm from 25∘C to 100∘C. Calculate ΔU,ΔH and the entropy change during the process.
View SolutionOne moles of an ideal gas which CV=3/2R is heated at a constant pressure of 1atm from 25∘C to 100∘C. Calculate ΔU,ΔH and the entropy change during the process.
View Solution
