An ideal gas at is enclosed in an adiabatic vertical cylinder havin an area of cross section between two light movable pistons as shown in figure. Spring with force constant is in a relaxed state initially. Now the lower position is moved upwards a distance , being the initial length of gas column . It is observed that the upper piston moves up by a distance . Final temperature of gas. Take for the gas to be .

The value of is
The correct Answer is:C
Final pressure,
Solving,
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
An ideal gas at NTP is enclosed in an adiabatic vertical cylinder havin an area of cross section A=27cm2 between two light movable pistons as shown in figure. Spring with force constant K=37−−N/m is in a relaxed state initially. Now the lower position is moved upwards a distance h/2, h being the initial length of gas column . It is observed that the upper piston moves up by a distance h/16. Final temperature of gas4/3×273K. Take γ for the gas to be 3/2.

When the lower pistone is moved upwards a distance h/2, the compression.
View SolutionAn ideal gas at NTP is enclosed in an adiabatic vertical cylinder havin an area of cross section A=27cm2 between two light movable pistons as shown in figure. Spring with force constant K=37−−N/m is in a relaxed state initially. Now the lower position is moved upwards a distance h/2, h being the initial length of gas column . It is observed that the upper piston moves up by a distance h/16. Final temperature of gas4/3×273K. Take γ for the gas to be 3/2.

When the lower pistone is moved upwards a distance h/2, the compression.
View SolutionAn ideal gas at NTP is enclosed in an adiabatic vertical cylinder havin an area of cross section A=27cm2 between two light movable pistons as shown in figure. Spring with force constant K=37−−N/m is in a relaxed state initially. Now the lower position is moved upwards a distance h/2, h being the initial length of gas column . It is observed that the upper piston moves up by a distance h/16. Final temperature of gas4/3×273K. Take γ for the gas to be 3/2.

Which of the following statements is correct ?
View SolutionA non conducting piston of mass m and area of cross section A is placed on a non conducting cylinder as shown in figure. Temperature, spring constant, height of the piston are given by T,K,h respectively. Initially spring is relaxed and piston is at rest. Find
(a) Number of moles
(b) Work done by gas to displane the piston by distance d when the gas is heated slowly.
(c ) Find the final temperature

View SolutionWhat force is applied on a piston of area of cross section 2cm2 to obtain a force 150 N on the piston of area of cross section 12cm2 in a hydraulic machine ?
View SolutionAn ideal gas is enclosed in a thermally insulated container. Container is covered by an insulating piston which is connected with spring. Small displacement is given to piston as shown in figure. Which of the following statements is correct? Neglect friction everywhere.
View Solution2 moles of a diatomic gas are enclosed in a cylinder piston arrangment. The area of cross section and mass of the piston are 1cm2 and 1 kg respectively. A heater is supplying heat to the gas very slowly. Find heat supplied (in joule) by the heater is the piston moves through a distance of 10 cm.
 .
.
View SolutionAn ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10cm2and weight 1kg. The length of the gas column in the vessel now taken into a spaceship revolving round the earth as satellite. The air pressure in the spaceship is maintained at 100kPa. Find the length of the gas column in the cylinder.
View SolutionAn incompressible liquid of density ρ is enclosed with two frictionless pistons one of cross-sectional area A and the other of 4 A. When the narrow piston moves out by a distance.
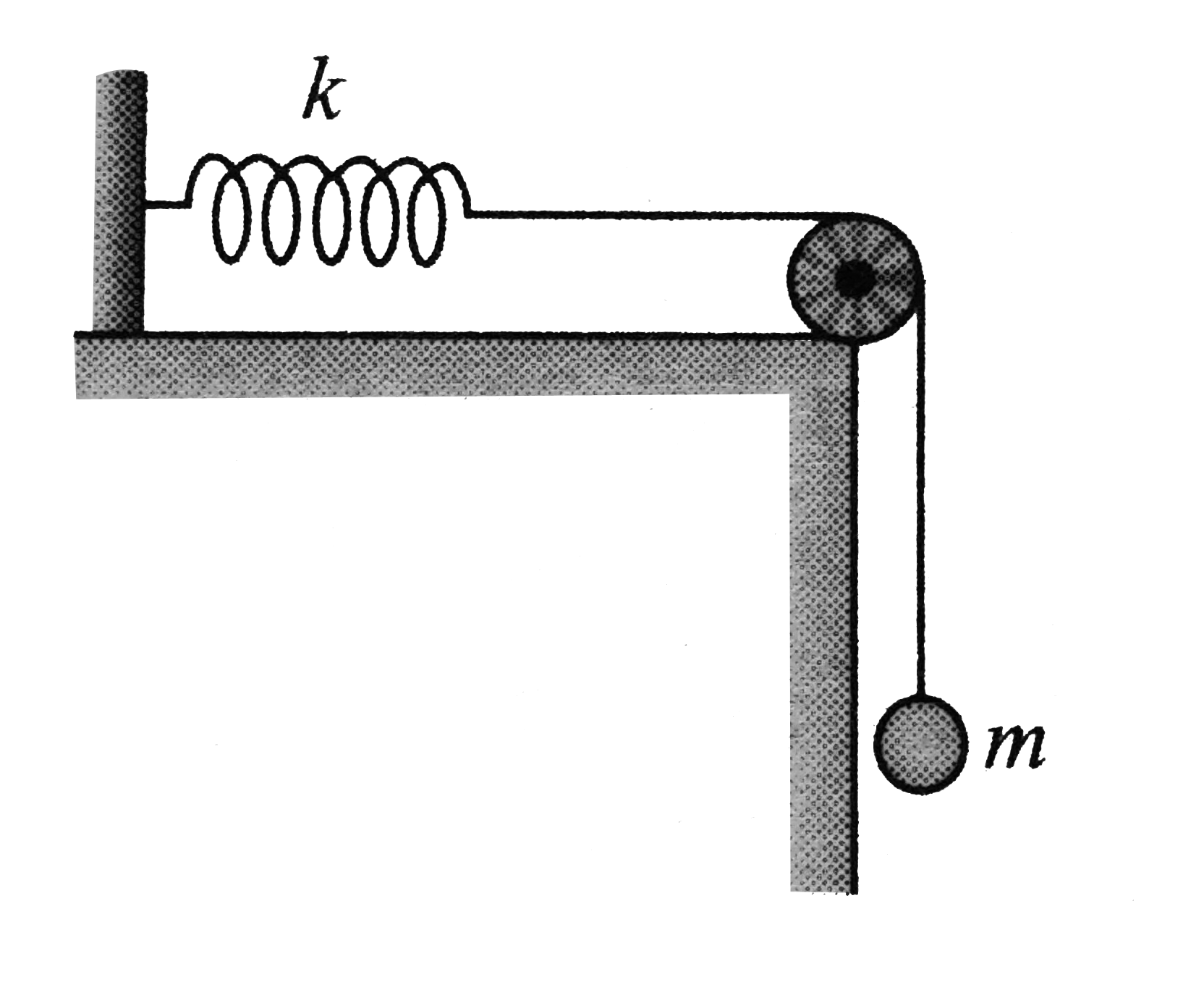
View SolutionIn figure, the light spring is of force constant k and is on a smooth horizontal surface. Initially the spring is relaxed. Calculate the work done by an external agent to lower the hanging body of mass M slowly, till it remains in equilibrium.
View Solution
