An ideal monoatomic gas following the process PV2= constant will have heat capacity 11RX. Find the value of X.
The correct Answer is:6
To solve the problem, we need to determine the value of X in the expression for the heat capacity of an ideal monoatomic gas undergoing a specific process defined by the equation PV2=constant.
1. Identify the Process:
The given process is PV2=constant. We can express this as P=kV−2, where k is a constant.
2. Use the Ideal Gas Law:
For an ideal gas, we have the equation PV=nRT. Substituting P from the previous step:
kV−2V=nRT⟹kV−1=nRT⟹V=knRT
3. Relate Pressure and Volume:
From P=kV−2, we can express pressure in terms of volume:
P=k(nRTk)−2=kn2R2T2k2=n2R2T2k
4. Determine the Work Done:
The work done W in a process can be calculated using the formula:
W=∫PdV
Since P=kV−2, we can integrate:
W=∫kV−2dV=−kV+C
5. Calculate the Heat Transfer:
The first law of thermodynamics states:
ΔU=Q−W
For an ideal monoatomic gas, the change in internal energy ΔU is given by:
ΔU=32nRΔT
6. Relate Heat Capacity to Process:
The heat capacity C for a process is defined as:
Q=CΔT
Therefore, we can write:
CΔT=ΔU+W
7. Substituting Values:
From the previous steps, we can substitute ΔU and W into the equation:
CΔT=32nRΔT−kV+C
8. Finding the Value of X:
After simplifying the equations and solving for C, we find that:
C=11XR
By comparing coefficients, we can deduce that:
X=2
Final Answer:
The value of X is 2.
The given process is PV2=constant. We can express this as P=kV−2, where k is a constant.
For an ideal gas, we have the equation PV=nRT. Substituting P from the previous step:
kV−2V=nRT⟹kV−1=nRT⟹V=knRT
From P=kV−2, we can express pressure in terms of volume:
P=k(nRTk)−2=kn2R2T2k2=n2R2T2k
The work done W in a process can be calculated using the formula:
W=∫PdV
Since P=kV−2, we can integrate:
W=∫kV−2dV=−kV+C
The first law of thermodynamics states:
ΔU=Q−W
For an ideal monoatomic gas, the change in internal energy ΔU is given by:
ΔU=32nRΔT
The heat capacity C for a process is defined as:
Q=CΔT
Therefore, we can write:
CΔT=ΔU+W
From the previous steps, we can substitute ΔU and W into the equation:
CΔT=32nRΔT−kV+C
After simplifying the equations and solving for C, we find that:
C=11XR
By comparing coefficients, we can deduce that:
X=2
The value of X is 2.
Topper's Solved these Questions
Similar Questions
One mole of an ideal monatomic gas undergoes the process P=αT1/2, where α is constant . If molar heat capacity of the gas is βR1 when R = gas constant then find the value of β.
View SolutionAn ideal monoatomic gas is taken through a process PVa = const. The value of 'a' for whichspecific heat capacity of the gas is zero is :-
View Solution
Knowledge Check
One mole of monoatomic ideal gas follows a proces AB, as shown. The specific heat of the process is 13R6. Find the value of x on P-axis.
 A4P0B5P0C6P0D8P0
A4P0B5P0C6P0D8P0One mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
ARΔTB3RΔTC5RΔTD6RΔTP-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
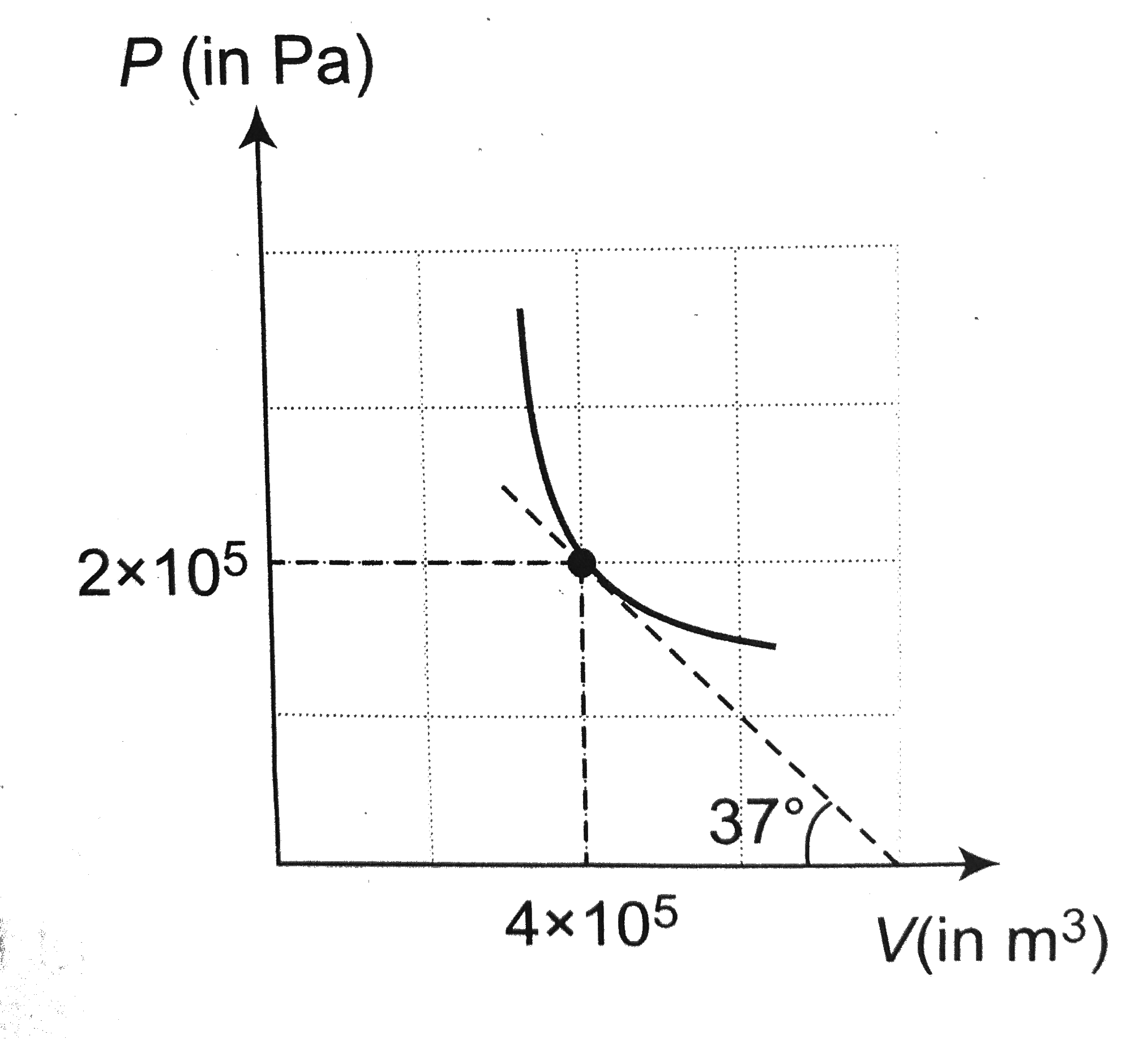 A34B−32C53D32
A34B−32C53D32
[" A monoatomic ideal gas follows the process: "],[TV^(32)=" constant "],[" The molar specific heat for this process is "((5R)/(y))." Where "R" is gas constant.Find the value of "2y "]
View SolutionAn ideal gas follows following process P^(2)V= constant.
Then on expansion, the tempereture of gas
View SolutionFor an ideal monoatomic gas, molar heat capacity at constant volume (Cv) is
View SolutionAn ideal monoatomic gas indergoes a pressure pVn=constant. The adiabatic constant for gas is y. During the process, volume of gas increases from V0 to rV0 and pressure decreases for p0 to p02r Based on above information, answer the following questios :
The of n is
View SolutionAn ideal monoatomic gas indergoes a pressure pVn=constant. The adiabatic constant for gas is y. During the process, volume of gas increases from V0 to rV0 and pressure decreases for p0 to p02r Based on above information, answer the following questios :
The molar heat capacity of the gas for the process is
View Solution

