An ideal gas follows following process P^(2)V= constant.
Then on expansion, the tempereture of gas
decreases
increases
remain constant
none of these
P2V= constant
PV=nRT
P=nRTV
P2V=(nRTV)2V
=(nRT)2V= constant
VαT2
increases in expansion
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY PART (A)
14 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY PART (B)
1 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Chemistry PART D
4 Videos
- SOLUTIONSBOOK - BANSALCHAPTER - SOLUTIONSEXERCISE - Exercise4
32 Videos
- THERMOCHEMISTRYBOOK - BANSALCHAPTER - THERMOCHEMISTRYEXERCISE - Exercise 4
15 Videos
Similar Questions
A given sample of an ideal gas follows the process V^(3)T^(2)= constant.Here V is the volume and T is the temperature both in SI units.The bulk modulus of the gas when its pressure becomes P is:
View SolutionAn ideal gas follows a process PVγ = constant where γ = adiabatic exponent.The slope of P-V graph will be represented by
View Solution
Knowledge Check
P-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
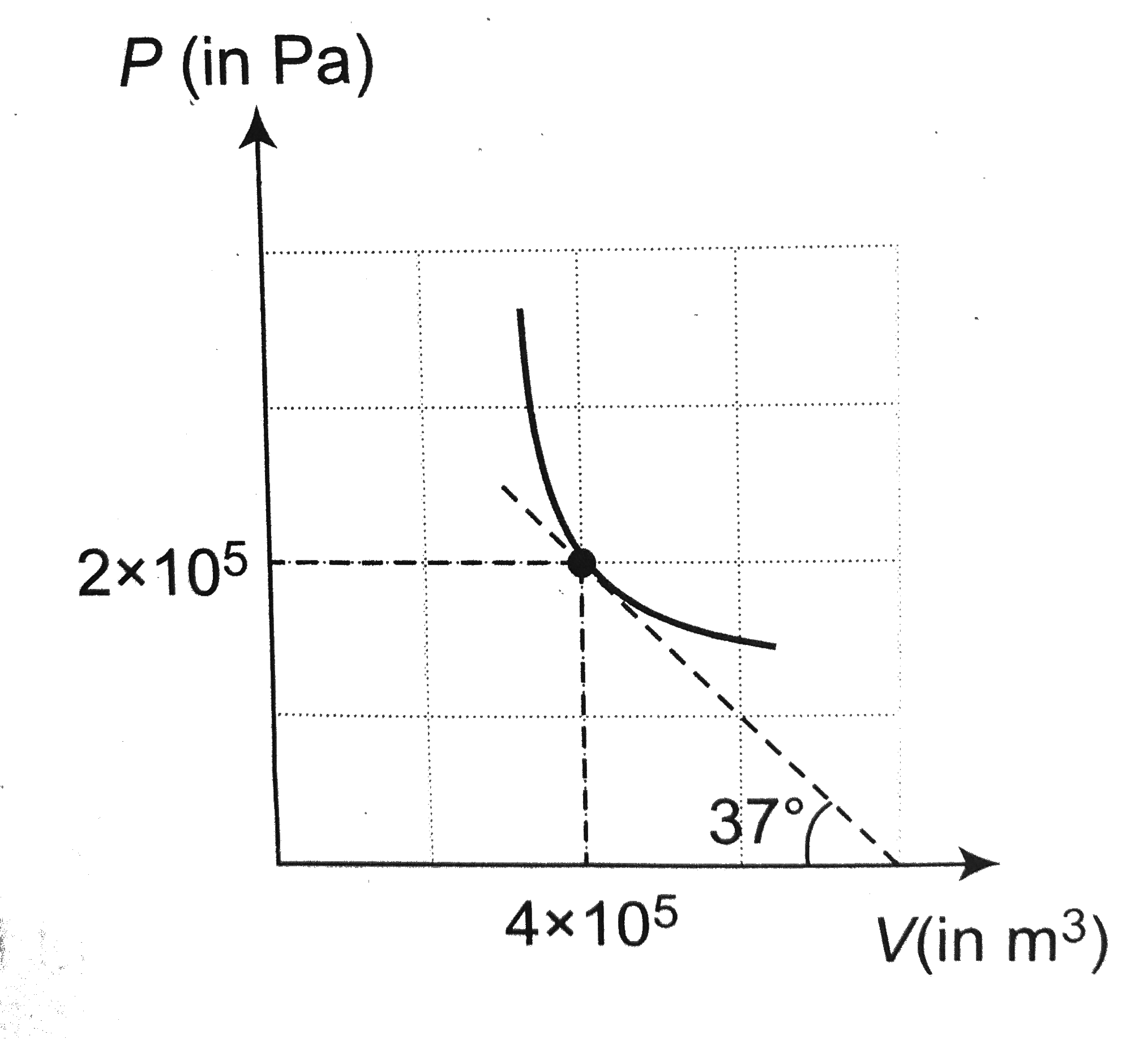 A34B−32C53D32
A34B−32C53D32An ideal gas is taken through a process PT3= constant. The coefficient of thermal expansion of the gas in the given process is
A1/TB2/TC3/TD4/TAn ideal gas is expanding such that PT2=constant. The coefficient of volume expansion of lthe gas is:
A1TB2TC3TD4T
An ideal gas is expanding such that PT3= constant . The coefficent of volume expansion of the gas is :
View SolutionAn ideal gas is expanding such that PT2= constant. The coefficient of volume expansion of the gas is AT, where T is temperature in Kelvin and P is pressure, Find the value of A.
View SolutionAn ideal gas is taken through a process PT3 = constant . The coefficient of thermal expansion of the gas in the given process in n/T. Find n.
View SolutionAn ideal gas is expanded such that PT2=a constant. The coefficient of volume expansion of the gas is
View SolutionAn ideal gas expands according to the law P2V = constant . The internal energy of the gas
View Solution
