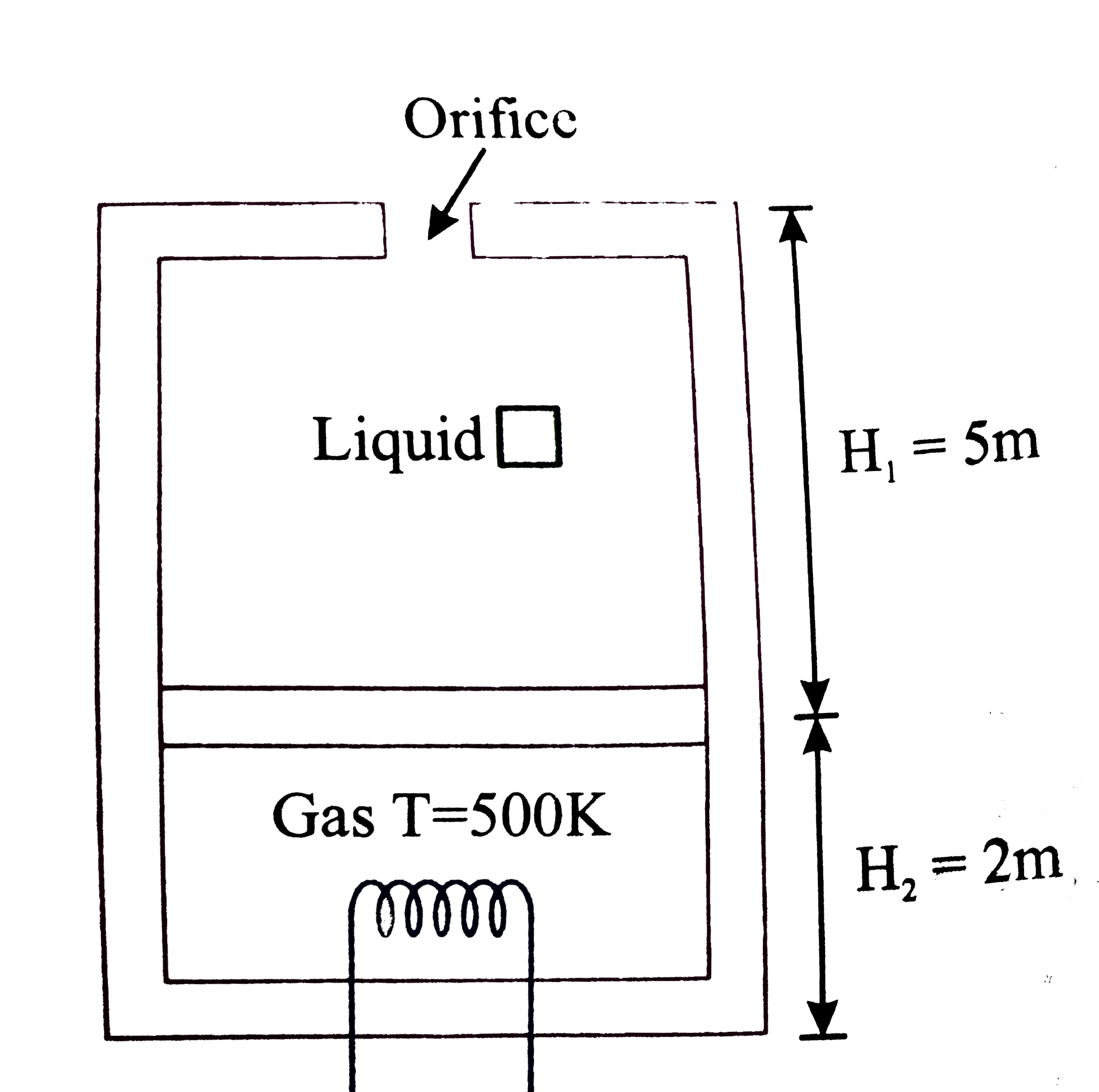
The system shown in the figure is in equilibrium. The piston is massless, frictionless and insulated. All walls of the chamber are also insulated. When heat is generated inside the lower chamber the piston slowly moves upwards by 2 m and the liquid comes out through an orifice so that it can rise to a maximum height of 5 m above the orifece level. The lower chamber contains 2 moles of an ideal monoatomic gas at 500k .
Area of orifice a =0.05m2
Area of the piston A=1m2
Density of the liquid, ρ=103kg/m3 , g=10m/s2
Atmospheric pressure, Patm=105N/m2
The final pressure of the gas is
1.8atm
0.18atm
1.5atm
none of these
The correct Answer is:A
Assume datum at the position of the orifice. Initial energy of the liquid
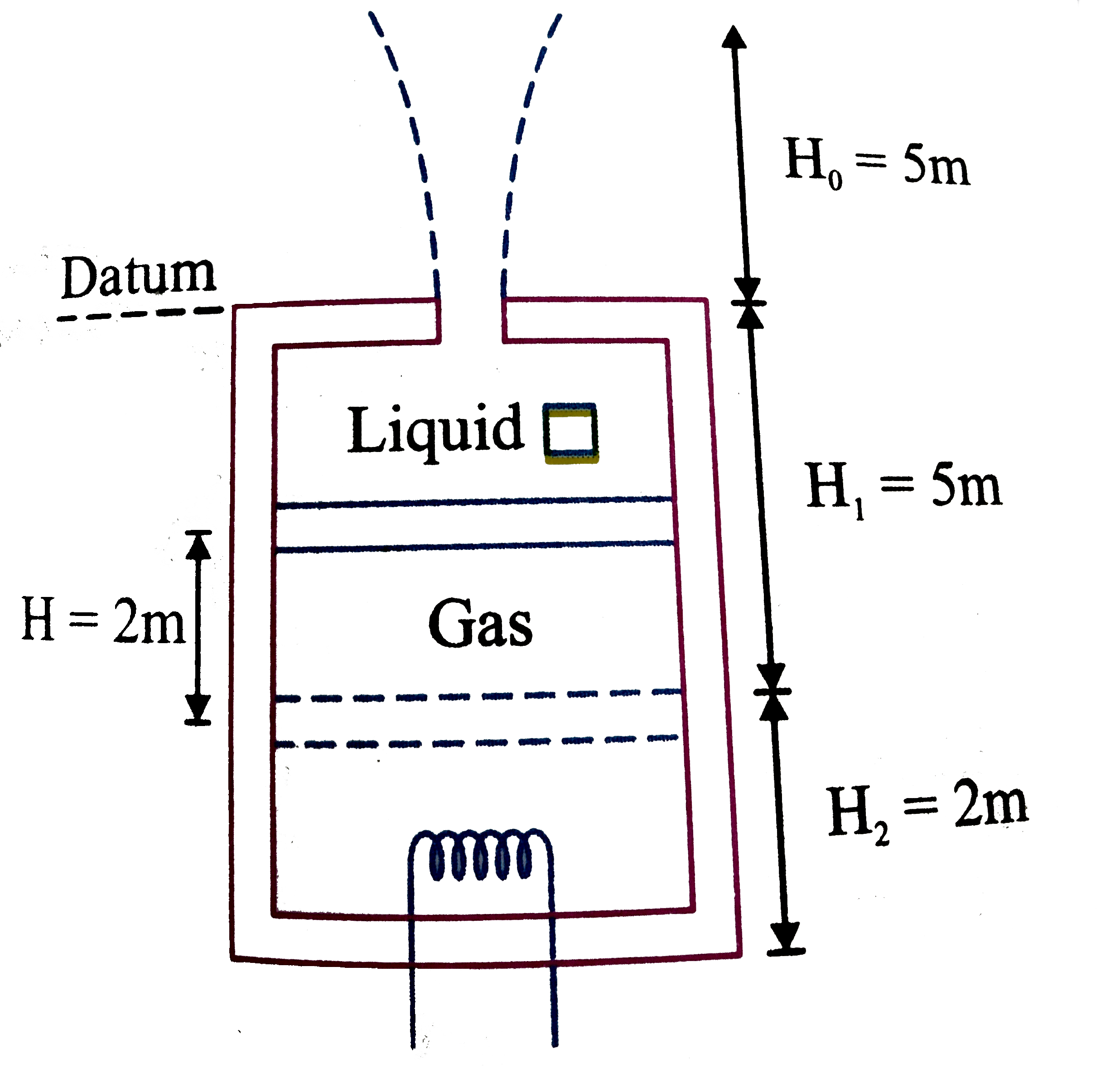
V=aA√2gh=0.051√2×10×5=0.5m/s
Ei=−12ρgAH21=12(103)(10)(52)=−1.25×105J
and final energy Er=−12ρA(H1−h)2+ρgAhh0
=−12(103)(10)(1)(5−1)2+(103)(10)(1)(5)
−0.45×105+105
Work done by the expanding gas is
W=Er−Ei=1.25×105−0.45×105+105
=1.8×105J
Initial pressure of the gas , p1=Patm+ρgH1
=105+(103)(10)(5)=1.5×105Pa
Final , pressure of the gas k,
p2=Patm+ρ(H1−h+h0)
=105+(103)(10)(5−2+5)=1.8×105Pa
Initial volume, V1=AH2=(1)(2)=2m3
Final volume, V2=A(H2+h)=(1)(2+2)=6m3
Sincep1V1T1=p2V2T2,orT2=p2V20p1V1T1=(1.8)(4)(1.5)(2)
T1=(1.8)(4)(1.5)(2)(500)
Increases in internal energy, ΔU=nCvΔT
here, n=2,Cv=3R2,ΔT=1200−500=700K
∴Δu(2)(3/2)(8,3)(700)=17.43kJ
Q=ΔU+W=17.43+180=197.43kJ
Time taken =2m0.5m/s=4s
Average power =197.43kJ4s=49.36KW
Topper's Solved these Questions
Similar Questions
The ratio of coefficients of apparent expansions of the same liquid in two different vessels is 1:2. If α1 and α2 are the coefficient of linear expansions then coefficient of real expansion of the liquid is
View SolutionThree metal rods of coefficient of thermal conductivities K,2K,3K conducts heats of 3Q,2Q,Q per seconds through unit area then the ratio of temperature gradients .
View SolutionA thermally insulated chamber of volume 2V0 is divided by a frictionless piston of area S into two equal part A and B. Part A has an ideal gas at pressrue P0 and temperature T0 and part B is vacuum. A massless spring of force constant K is connected with the piston and the wall of the container as shown. Initially the spring is unstretched. The gas inside chamber A is allowed to expand. Let in equilibrium the spring be compressed by x0. Then

View SolutionThe system shown in the figure is in equilibrium. The piston is massless, frictionless and insulated. All walls of the chamber are also insulated. When heat is generated inside the lower chamber the piston slowly moves upwards by 2 m and the liquid comes out through an orifice so that it can rise to a maximum height of 5 m above the orifece level. The lower chamber contains 2 moles of an ideal monoatomic gas at 500k . Area of orifice a =0.05 m ^(2) Area of the piston A=1 m^(2) Density of the liquid, rho=10^(3) kg//m^(3) , g=10 m//s^(2) Atmospheric pressure, P_(atm)=10^(5) N//m^(2) The speed of piston is
View SolutionThe system shown in the figure is in equilibrium. The piston is massless, frictionless and insulated. All walls of the chamber are also insulated. When heat is generated inside the lower chamber the piston slowly moves upwards by 2 m and the liquid comes out through an orifice so that it can rise to a maximum height of 5 m above the orifece level. The lower chamber contains 2 moles of an ideal monoatomic gas at 500k . Area of orifice a =0.05 m ^(2) Area of the piston A=1 m^(2) Density of the liquid, rho=10^(3) kg//m^(3) , g=10 m//s^(2) Atmospheric pressure, P_(atm)=10^(5) N//m^(2) The average power of the heater is
View SolutionFigure shows a long cylindrical container with ideal gas in two chambers. Lower chamber is filled with one mole of a mono atomic gas, while upper chamber has one mole of a diatomic gas. The gases initially are at temperature 300K, the container walls as well as pistons are conducting. Both the pistons are identical with mass 'M' and area 'A' such that MgA=P0 (atmosphere pressure).
Assuming the ideal gas constant to be R, answer the following questions:

The upper piston is pulled up slowly by 16cm and held there. the displacement of the lower piston till it reaches new equilibrium state is:
View SolutionFigure shows a long cylindrical container with ideal gas in two chambers. Lower chamber is filled with one mole of a mono atomic gas, while upper chamber has one mole of a diatomic gas. The gases initially are at temperature 300K , the container walls as well as pistons are conducting. Both the pistons are identical with mass 'M' and area 'A' such that (Mg)/A=P_(0) (atmosphere pressure). Assuming the ideal gas constant to be R , answer the following questions: Total work done by the ideal gases in this process is
View SolutionAn adiabatic cylindrical chamber with a frictionless movable piston has been placed on a smooth horizontal surface as shown. One mole an ideal monotonic gas is enclosed inside the chamber. Mass of the piston is M and mass of the remaining chamber including the gas is 4 M. The gas is at atmospheric pressure and temperature. A particle of mass M moving horizontally with speed v, strikes the piston elastically. Find the change in temperature of the gas when the compression is maximum.
View SolutionOne mole of a monoatomic ideal gas occupies two champers of a cylinder partioned by means of a movable pision. The walls of the cylinder as well as the piston are thermal insulators. Initially equal amounts of gas fill both the chambers at (P0,V0,T0). A coil is burnt in the left chamber which absorbs heat and expands , pushing the piston to the right . The gas on the right chamber is compressed until to pressure becomes 32P0.
_S01_110_O01.png)
The final volume of left chamber is
View SolutionOne mole of a monoatomic ideal gas occupies two champers of a cylinder partioned by means of a movable pision. The walls of the cylinder as well as the piston are thermal insulators. Initially equal amounts of gas fill both the chambers at (P0,V0,T0). A coil is burnt in the left chamber which absorbs heat and expands , pushing the piston to the right . The gas on the right chamber is compressed until to pressure becomes 32P0.
_S01_111_O01.png)
The work done on the gas in the right chamber is
View SolutionAs shown , a piston chamber pf cross section area A is filled with ideal gas. A sealed piston of mass m is right at the middle height of the cylinder at equilibrium. The friction force between the chamber wall and the piston can be ignored . The mass of the rest of the chamber is M.The atmosphere pressure is P0. Now slowly pull the piston upwards , find the maximum value of M such that the chamber can be lifted off the ground. The temperature remains unchanged.
_E01_049_Q01.png)
View SolutionThe two lower thick walled chambers of heart are called _______.
View SolutionAt equilibrium which chamber will have lower water potential ?
View SolutionS is a piston of mass M which can slide inside a cylinder without friction. The walls of the cylinder is adiabatic and the piston is diathermic and area of cross section of cylinder is A. Length of the cylinder is 2l_0 . Initial pressure of each chamber is P_0 . Volume of the chambers are equal. Initially spring is unstretched and has spring constant k. The spring is fixed with piston and wall of the cylinder as shown in the figure. Find out its time period when piston is given small displacement.
View SolutionA highly conducting chamber contains air at a pressure of 75cm of Hg. The chamber is divided into two halves by a conducting piston fitted with a handle. The chamber is completely air tight. The piston by means of the

handle is slowly pulled towards right half way. The pressure difference across the piston will be:
View Solution
