An ideal monoatomic gas (γ=53) goes through a cyclic process consisting two isochoric and two isobaric lines. The absolute temperature of the gas rises two times both in isochoric heating and isobaric expansion. If number of moles are three, find efficiency of cyclic process.
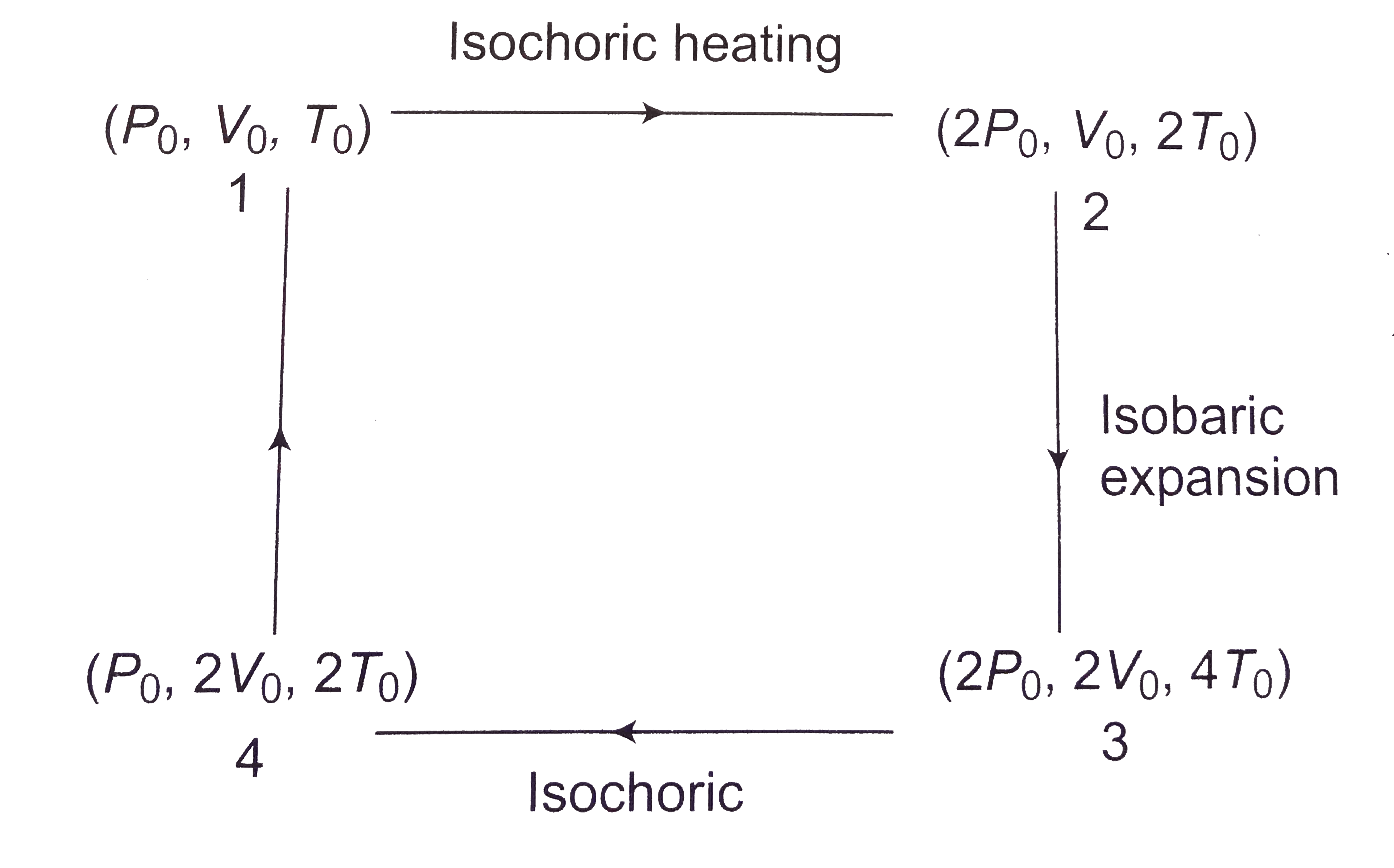
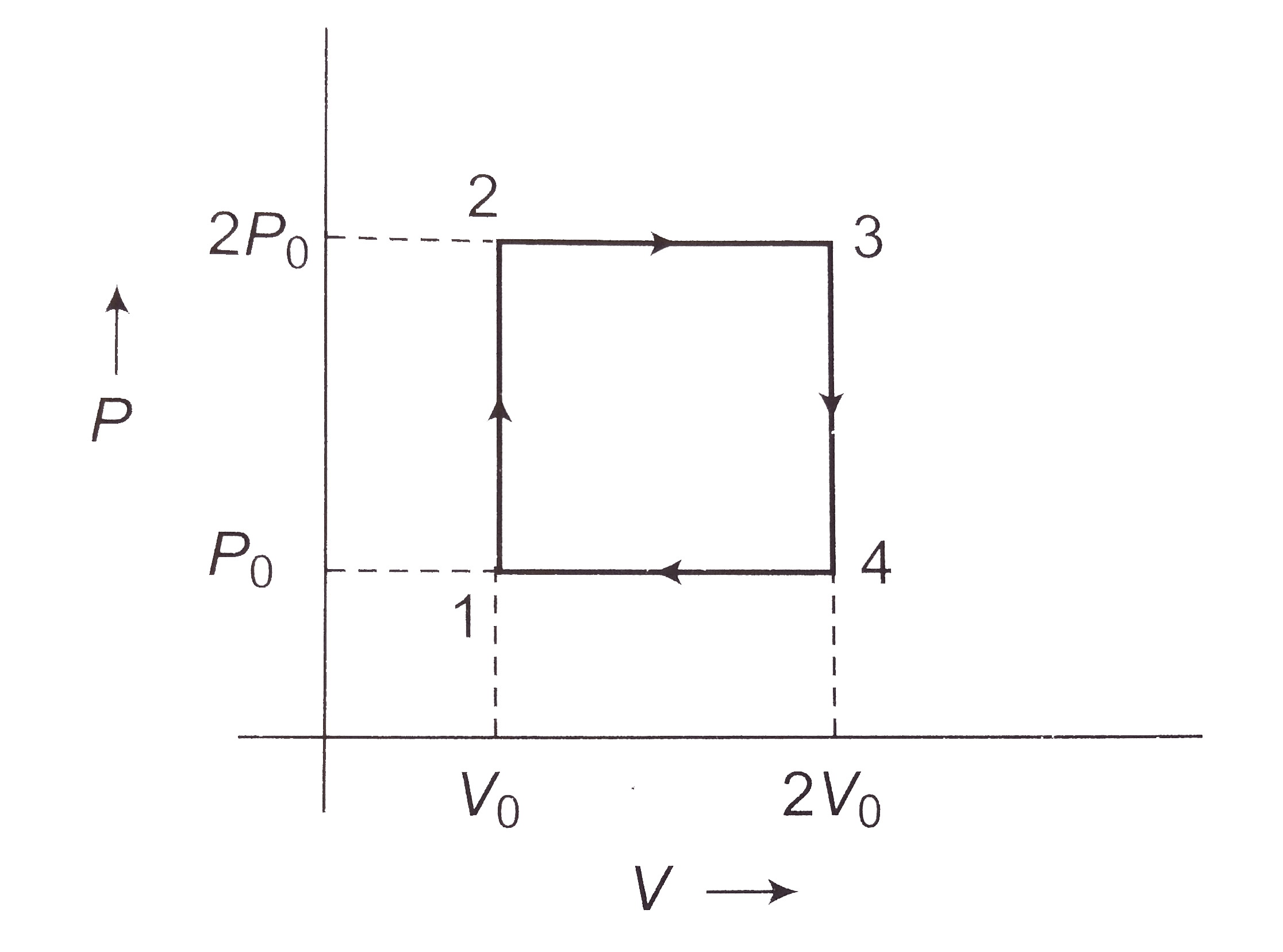
First sketch the process on P−V diagram.
Let initial thermodynamic coordinates are (P0,V0,T0)
ΔWcyclic=P0V0=3RT0
ΔQ1→2=nCV(T2−T1)=3.3R2(2T0−T0)=9RT2
ΔQ2→3=nCP=(T3−T2)=3.5R2(4T0−2T0)
=15RT0
ΔQ3→4=−ve,ΔQ4→1=−ve
Efficiency η=ΔWcyclicHeat supplied=ΔWcyclicΔQ1→2+ΔQ2→3
=3RT092RT0+15RT0=639=213
η=213×100=20013%
Topper's Solved these Questions
Similar Questions
An ideal gas whose adiabatic exponent equals γ goes through a cycle consisting of two isochoric and two isobaric lines. Find the efficiency of such a cycle, if the absolute temperature of the gas rises n times both in a isochoric heating and in the isobaric expansion.
View SolutionFind the efficiency of a cycle consisting of two isochoric and two adiabatic lines if the volume of the ideal gas changes n=10 times within the cycle. The working gas has γ=1.5.
View Solution
Knowledge Check
Helium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)
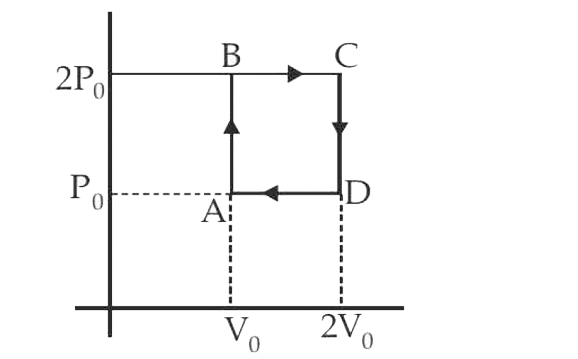 A15.4%B9.1%C10.5%D12.5%
A15.4%B9.1%C10.5%D12.5%One mole of an ideal monoatomic gas is taken through a cyclic process as shown. Choose the correct option(s).
 AWork done in process CA is RT0ln3.BHeat given to the gas in process CA is RT0ln3CThe magnitude of change in internal energy in process AB and BC must be sameDThe change in internal energy in process AB is negative.
AWork done in process CA is RT0ln3.BHeat given to the gas in process CA is RT0ln3CThe magnitude of change in internal energy in process AB and BC must be sameDThe change in internal energy in process AB is negative.Helium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)
 A15.4%B9.1%C10.5%D12.5%
A15.4%B9.1%C10.5%D12.5%
Find the efficiency of a cycle consisting of two isochoric and two adiabatic lines, if the volume of the ideal gas changes n=10 times within the cycle. The working substance is nitrogen.
View SolutionAn ideal monoatomic gas goes through a cyclic process. Ratio of maximum temperature and minimum temperature is 2. find efficiency of cycle.
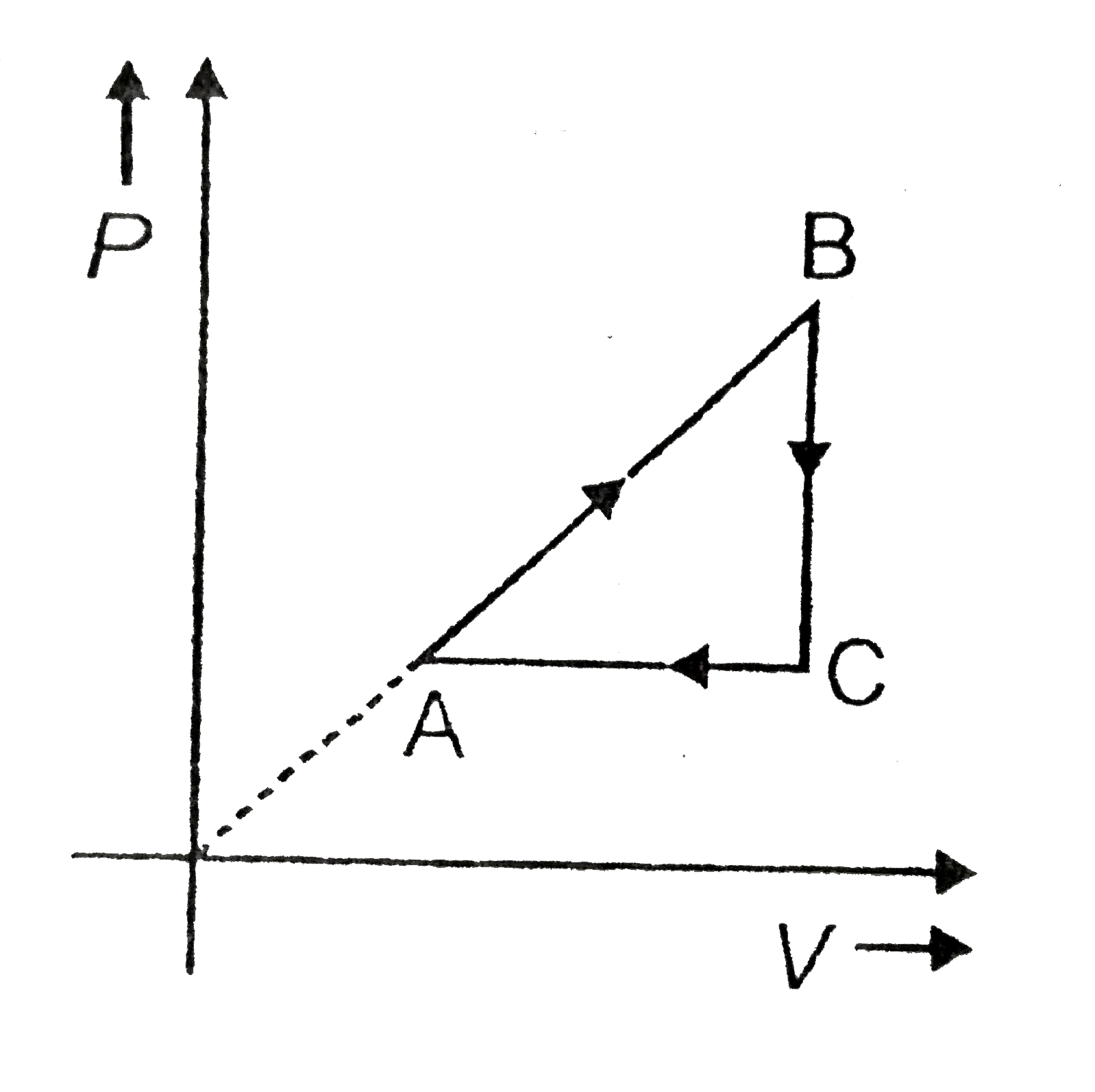 .
.
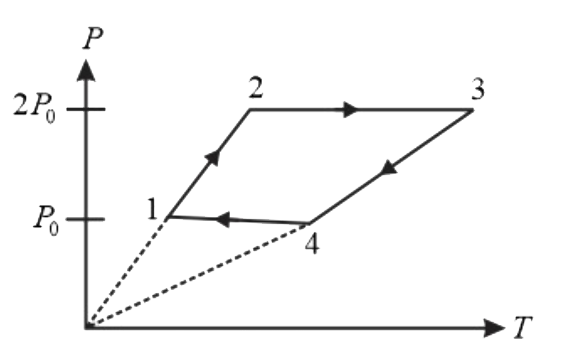
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process, as shown in the figure. If the temperature of the gas at state 1 is 300 K and at state 4 is 500 K, then heat exchanged during process 2→3, is
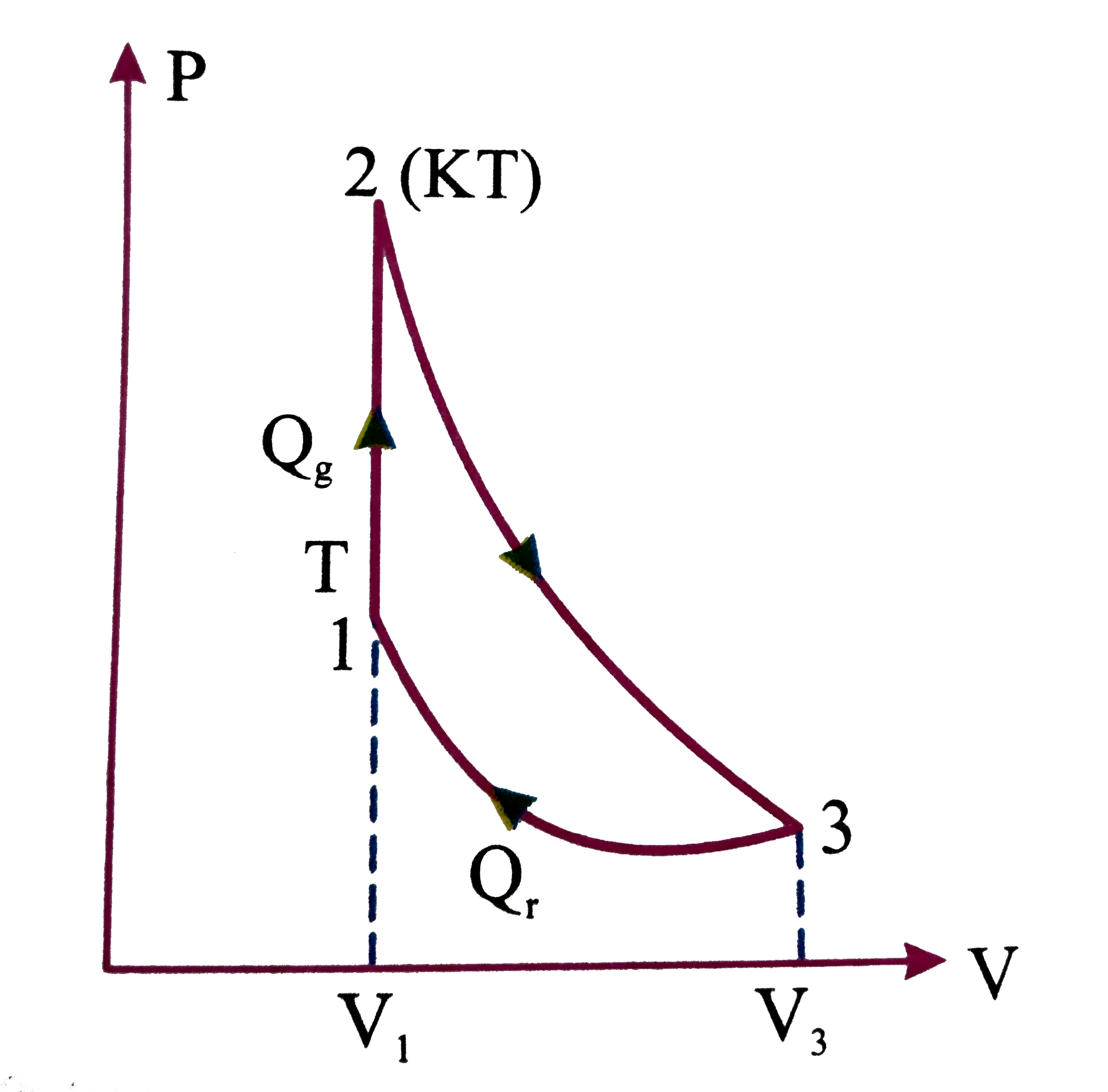
View SolutionAn ideal gas goes through a cycle consisting of ischoric adiabatic and isothermal lines. The isothermal process is perform at minimum temperature. If the absolute temperature varies K times with tn the cycle then find out its effcincy.
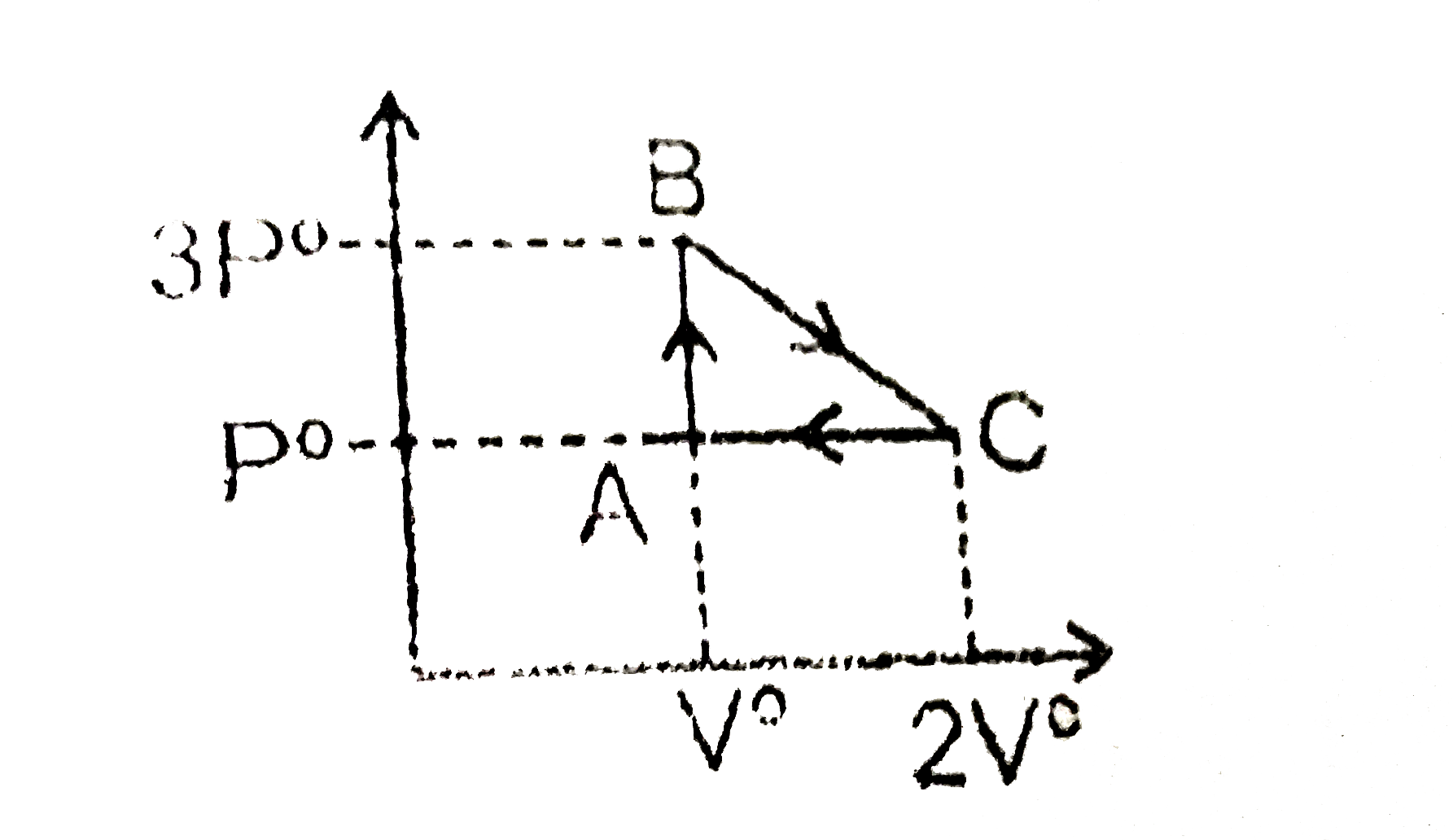
View SolutionOne mole of ideal monatomic gas is carried through the reversible cyclic process as shown in figure. Calculate the max temperature attained by the gas during the cycle.
View Solution
