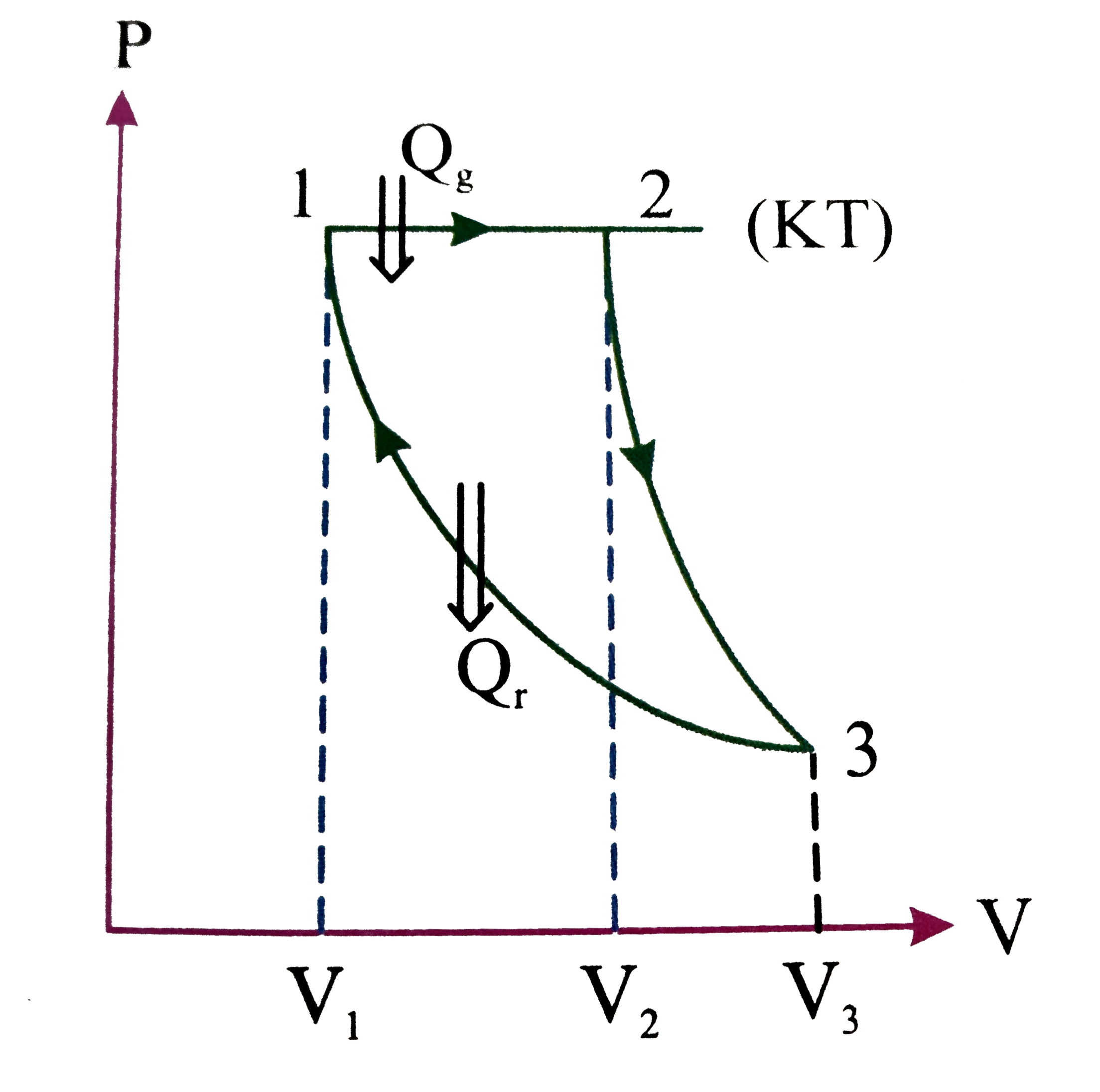
A cycle is made of three process is iso barie, adiabatic and isothermal. Isothermal process has minimum temperature. Absolute temperature charges by k times withing the cycle. Find out the efficiency.
1−1nK(K−1)
1+1nK(K−1)
1+1nK(K+1)
none of these
The correct Answer is:A
Qg=nCp(KT−T)
Qr=nRTinV3V1,V3V2V1V2=(K)1γ−11K
Process 1→2 is isobaric,
V1T=V2KTV3V1=K(K)1γ−1
Process 2→3 is adiabatic, KTVγ−12=TVγ−13
V3V2=(K)1γ−1KTVγ−12=TVγ−13
η=1RinV3/V1γRγ−1(K−1)=1−inK(K−1)
Topper's Solved these Questions
Similar Questions
An ideal gas goes through a cycle consisting of
(a) isochoric, adiabatic, and isothermal lines ,
(b) isobaric, adiabatic, and isothermal lines,
with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the absolute temperature varies n−fold within the cycle.
View SolutionAn ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies n−fold within the cycle.
View Solution
Knowledge Check
An ideal gas goes through a cycle consisting of ischoric adiabatic and isothermal lines. The isothermal process is perform at minimum temperature. If the absolute temperature varies K times with tn the cycle then find out its effcincy.
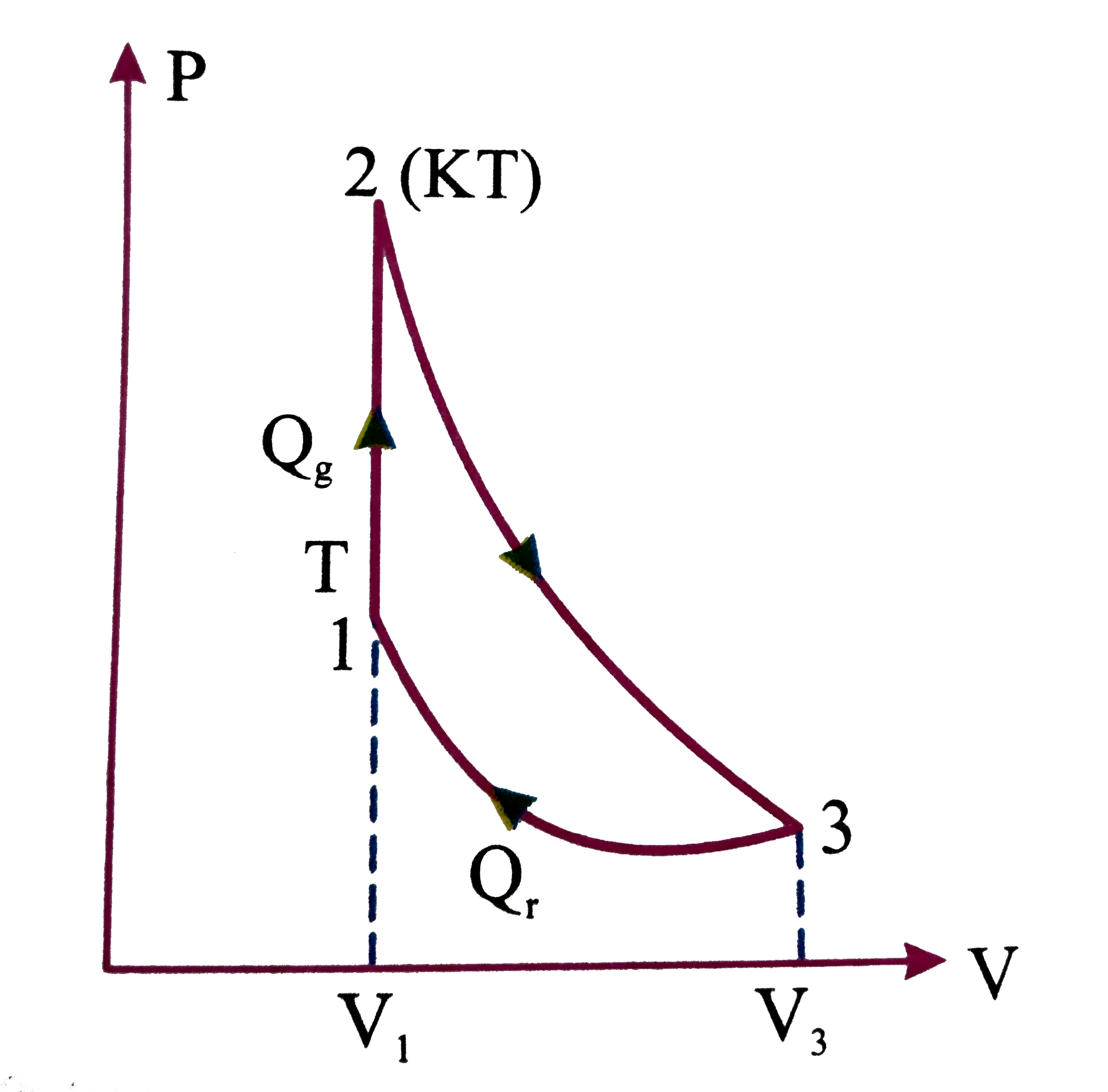 A1−lnKlB1+lnKlClnKlDllnK
A1−lnKlB1+lnKlClnKlDllnK
n moles of a monoatomic gas undergoes a cyclic process ABCDA as shown. Process AB is isobaric, process BC is adiabatic process CD is isochoric and process DA is isothermal the maximum temperature and minimum temperature in cycle are 4T0 and T0 respectively. Then:ATB>TC>TDBheat is released by the gas in the process CDCgeat is supplied by the gas to the surrounding in the process ABDheat is supplied to the gas to the surrounding in the process AB
Find the efficiency of a cycle consisting of two isobaric and two isothermal lines if the pressure varies n−fold and the absolute temperature τ−fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
View SolutionAn ideal monoatomic gas goes through a cyclic process. Ratio of maximum temperature and minimum temperature is 2. find efficiency of cycle.
 .
.
View SolutionOne mole of a monoatomic gas behving ideally is used as
working substance in an engine working in the cycle as shown
in the figure . The process AB, BC, CD and DA are respectively
reversible isobaric, adiabatic isochoric and isothermal . The ratio
of maximum to volume and temperature during the
cycle is 8√2 and 4 respectively. If the maximum T is 800 K
and γ=5/3. Calculate ΔE (in kJ) for the process BC.
Given R=8.3J/K−mol.
View Solutionn moles of a diatomic gas has undergone a cyclic process ABC as shown in figure. Temperature at A is T0. Find
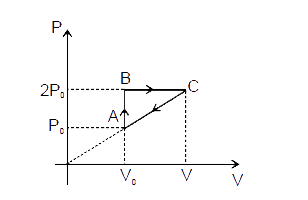
Find out the efficiency
View SolutionState true or false. Wrk done by an ideal gas in aiabatic expansion is less than that in isothermal process (for same temperature range)
View SolutionThe efficiency of the cycle shown below in the figure ( consisting of one isobar , one adiabatic and one isotherm ( is 50 % the ratio ,x, between the highest and lowest temperature attained in this cycle obeys ( the working substance is an ideal gas )
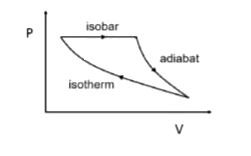
View Solution

