A rod AB of mass 3m and length 4a is falling freely in a horizontal position and c is a point distance a from A. When the speed of the rod is u, the point c collides with a particle of mass m which is moving vertically upwards with speed u. if the impact between the particle and the rod is perfectely elastic find
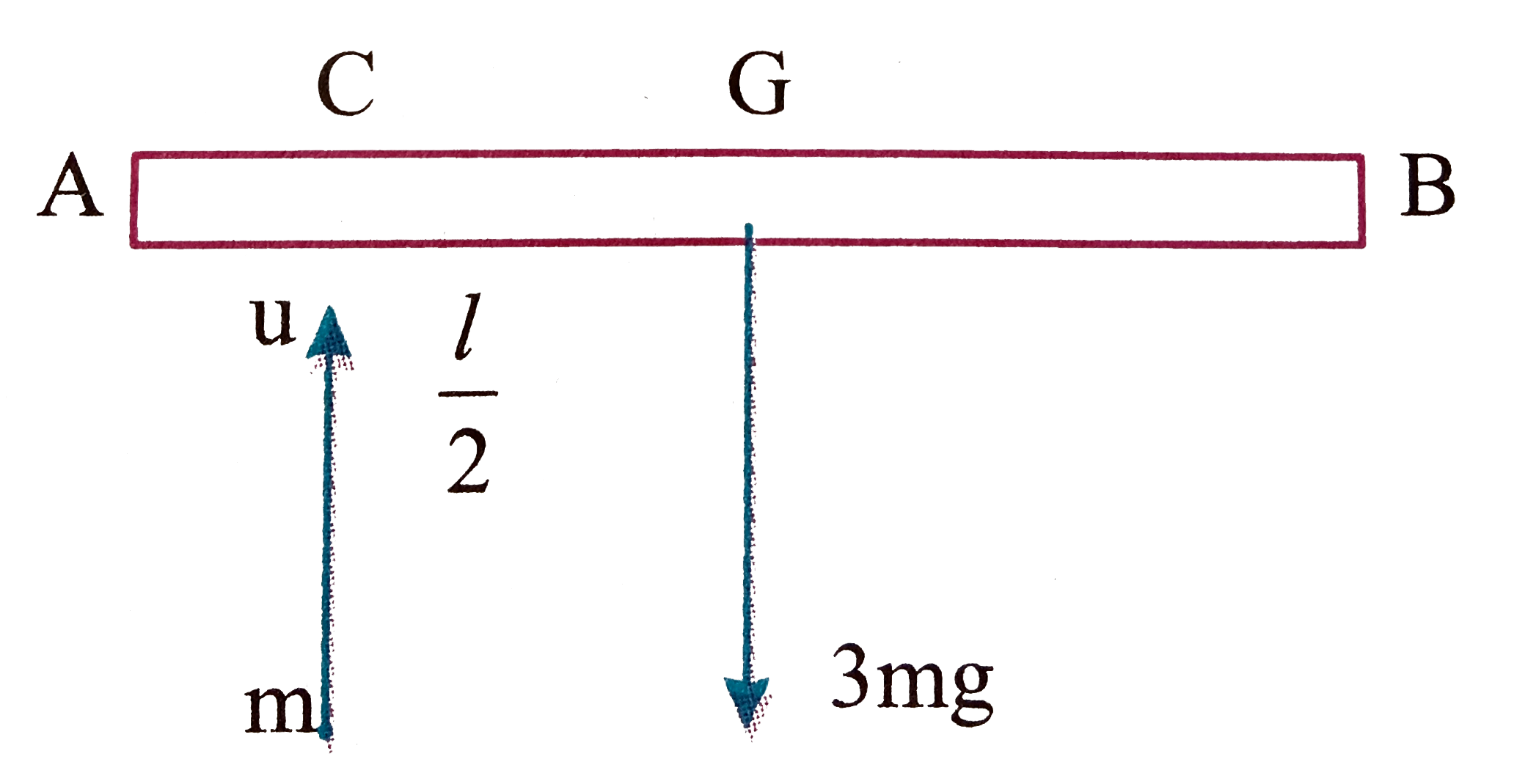
The velocity of the particle immediately after the impact
2919udown
1929udown
2919,uup
2719udown
The correct Answer is:A
In order to use the law of restitution. We need the speed of point C, which is u1−aω (down wards)

law of restitution now given relative velocity of separation at point of impact =e(relative velcity of approch) or u2−(u1−aω)=e(u+u)
hence 2u=u2−u1+aω
For the rod the speed of the particle is 2919υ (down wards)
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A rod of mass m and length l is held vertically on a smooth horizontal floor. Now it is released from this position, find the speed of its centre of mass when it makes an angle θ with the vertical.
View SolutionA uniform rod AB of mass 3m and length 2l is lying at rest on a smooth horizontal table with a smooth vertical axis through the end A. A particle of mass 2m moves with speed 2u across the table and strikes the rod at its mid-point C if the impact is perfectly elastic. Find the speed of the particle after impact if
(a). It strikes rod normally,
(b). Its path before impact was inclinded at 60∘ to AC.
View Solution
Knowledge Check
A rod AB of mass 3m and length 4a is falling freely in a horizontal position and c is a point distance a from A. When the speed of the rod is u, the point c collides with a particle of mass m which is moving vertically upwards with speed u. if the impact between the particle and the rod is perfectely elastic find
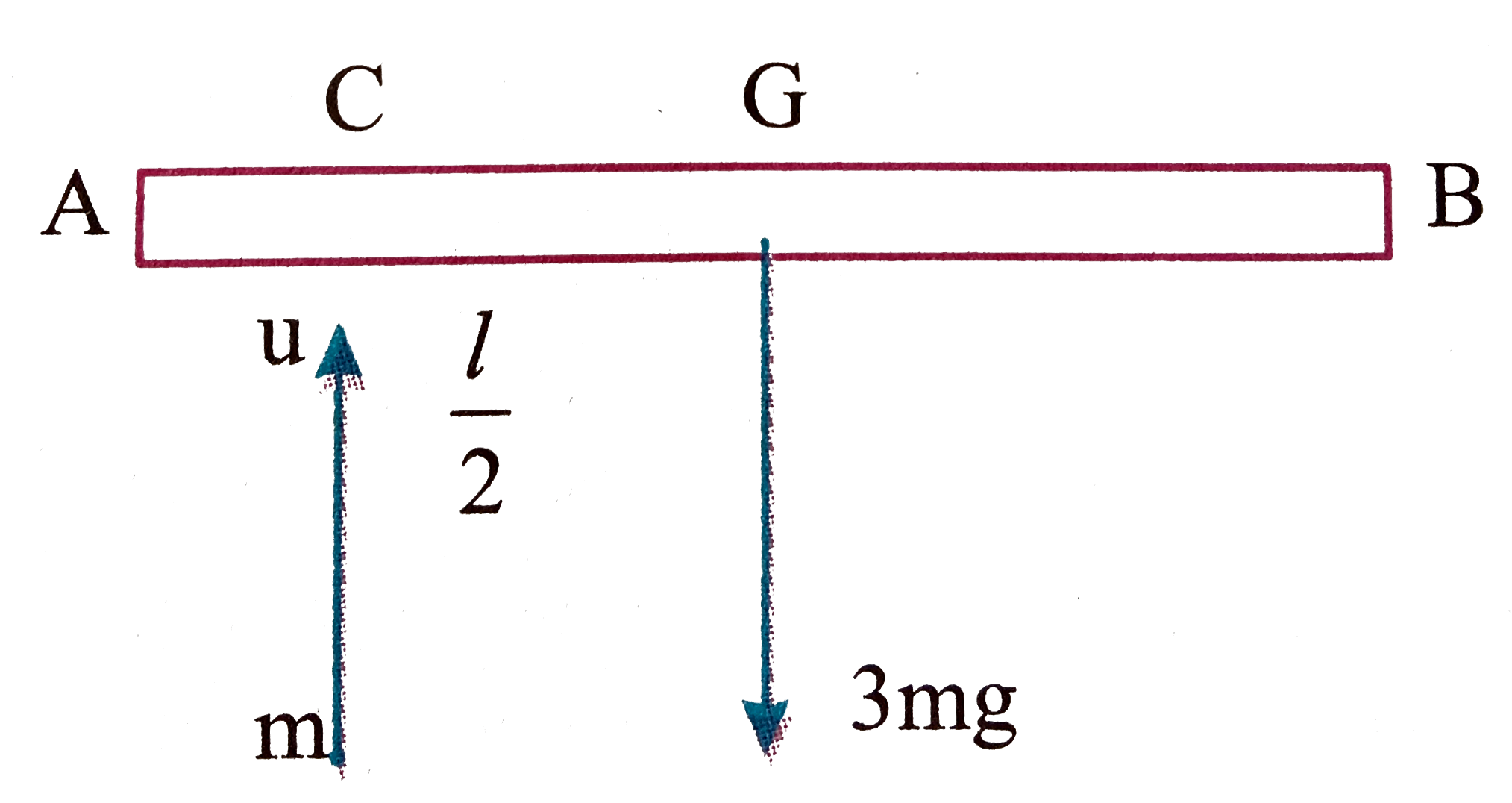
The angular velocity of the rod immediately after the impactA19u12aB12u19aC29u19aD19u29aA rod AB of mass 3m and length 4a is falling freely in a horizontal position and c is a point distance a from A. When the speed of the rod is u, the point c collides with a particle of mass m which is moving vertically upwards with speed u. if the impact between the particle and the rod is perfectely elastic find
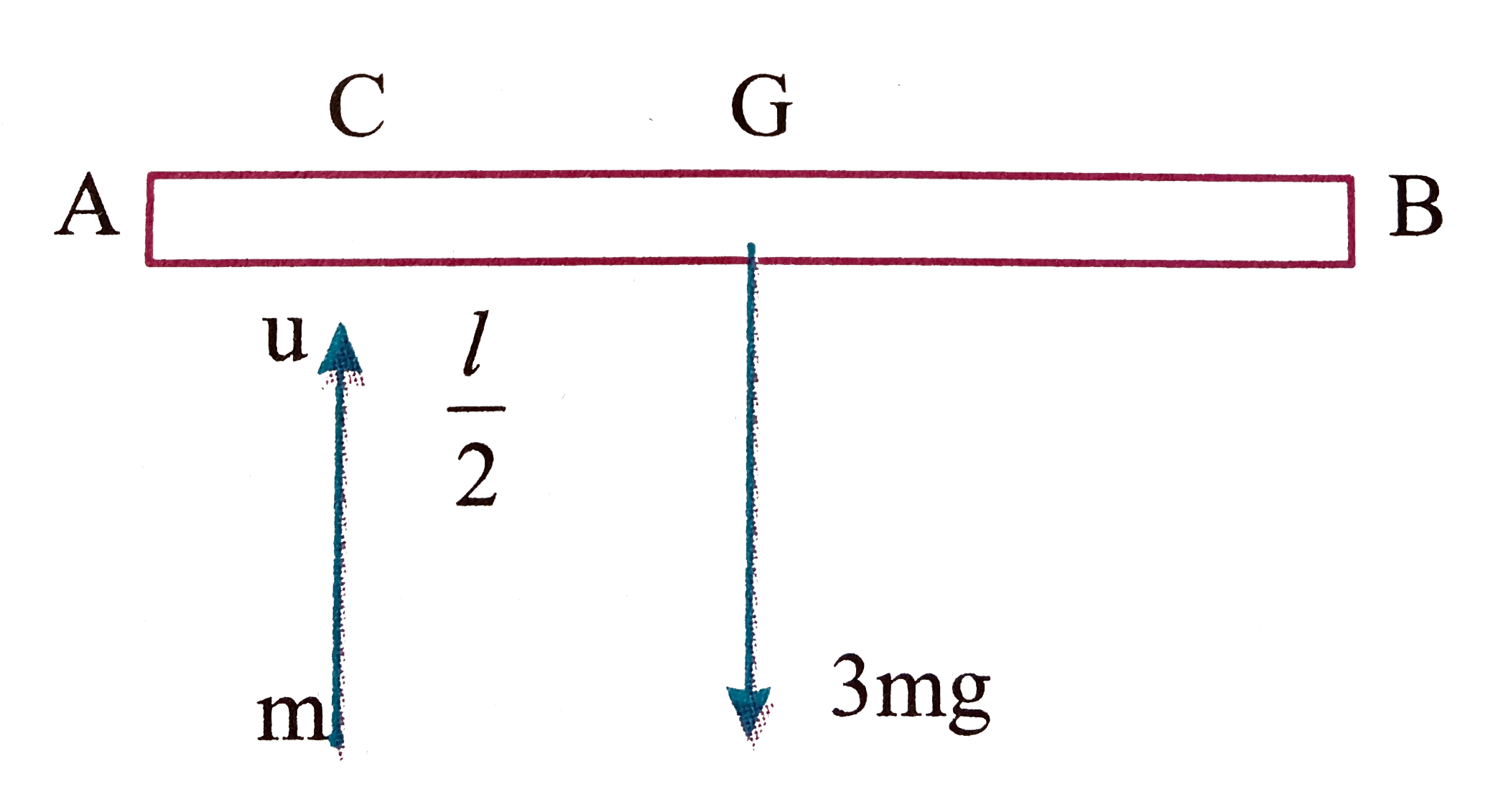
The speed of B immediately after the impact isA1927udownB1927uupC2719udownD2719uupA uniform rod AB of mass m and length 2a is falling freely without rotationb under gravity with AB horizontal. Suddenly the end A is fixed when the speed of the rod is v. The angular speed which the rod begains to rotate is
Av2aB4v3aCv3aD3v4a
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision.
View SolutionA uniform rod AB of mass m length 2a is allowed to fall under gravity with AB in horizontal. When the speed of the rod is v suddenly the end A is fixed. Find the angular velocity with which it begins to rotate.
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collision
View SolutionA uniform rod of mass M is hinged at its upper end. A particle of mass m moving horizontally strikes the rod at its mid point elastically. If the particle comes to rest after collision find the value of M/m?
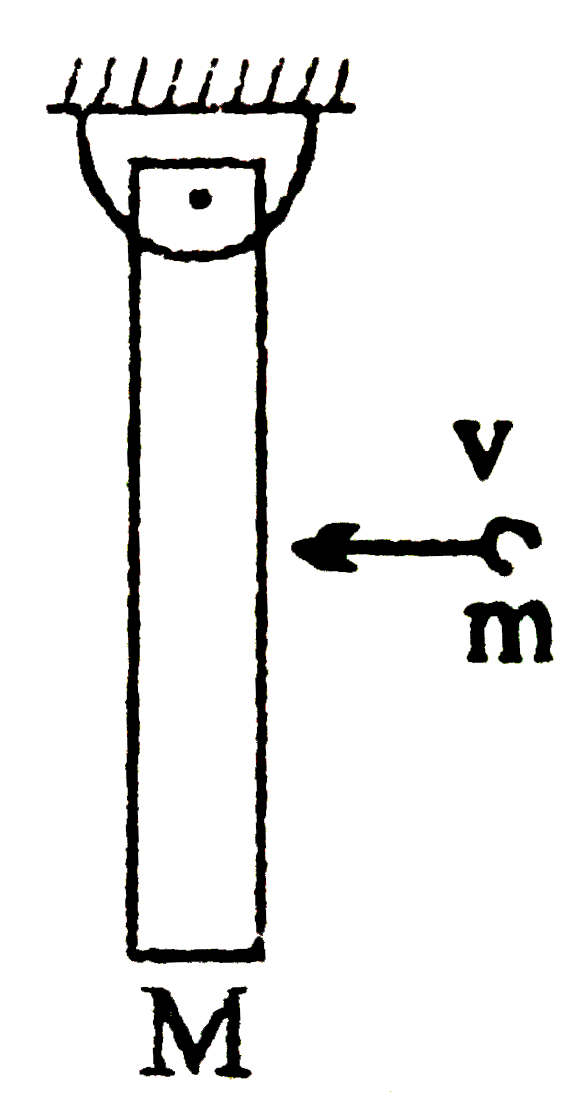
View Solution

