An uniform rod of mass and length is free to rotate about a horizontal axis passing through its centre. A particle of mass falls vertically through a height and collides elastically with the rod at a distance from . at the instant of collision the rod was stationary and was at angle with horizontal as shown in figure
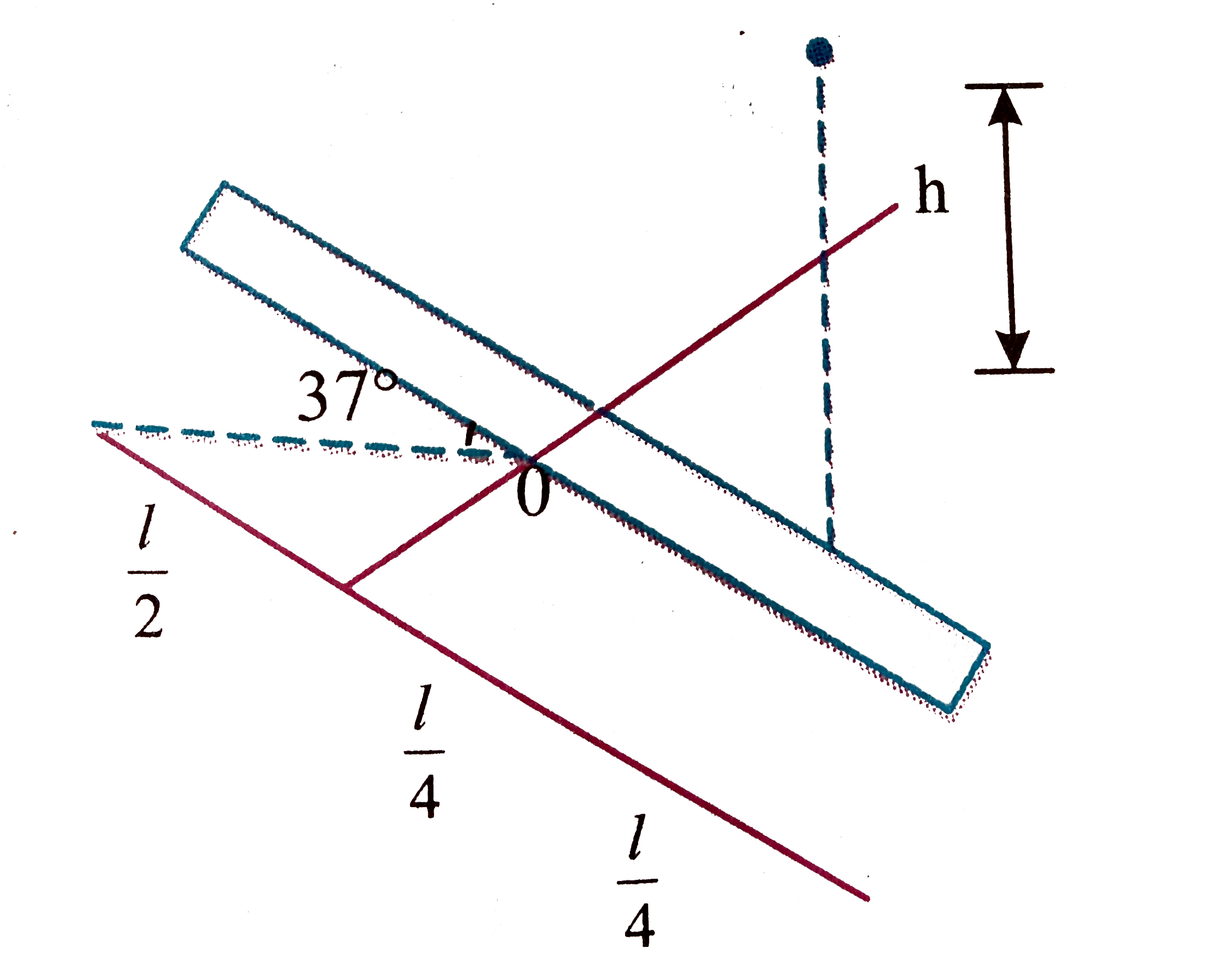
Velocity of particle after collision
The correct Answer is:C
Velcity component of particle, normal to rod(just after collision) is
Since, the collision is elastic, therefore, there is normal loss of kinetic energy during collision. Hence kinetic energy of system of rod and particle just after collision=kinetic energy of particle just before collision.
From equation tangential component of velocity of particle
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions

A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
View Solution
Knowledge Check
An uniform rod of mass m=30kg and length l=0.80m is free to rotate about a horizontal axis O passing through its centre. A particle P of mass M=11.2kg falls vertically through a height h=36245m and collides elastically with the rod at a distance l4 from O. at the instant of collision the rod was stationary and was at angle α=37∘ with horizontal as shown in figure
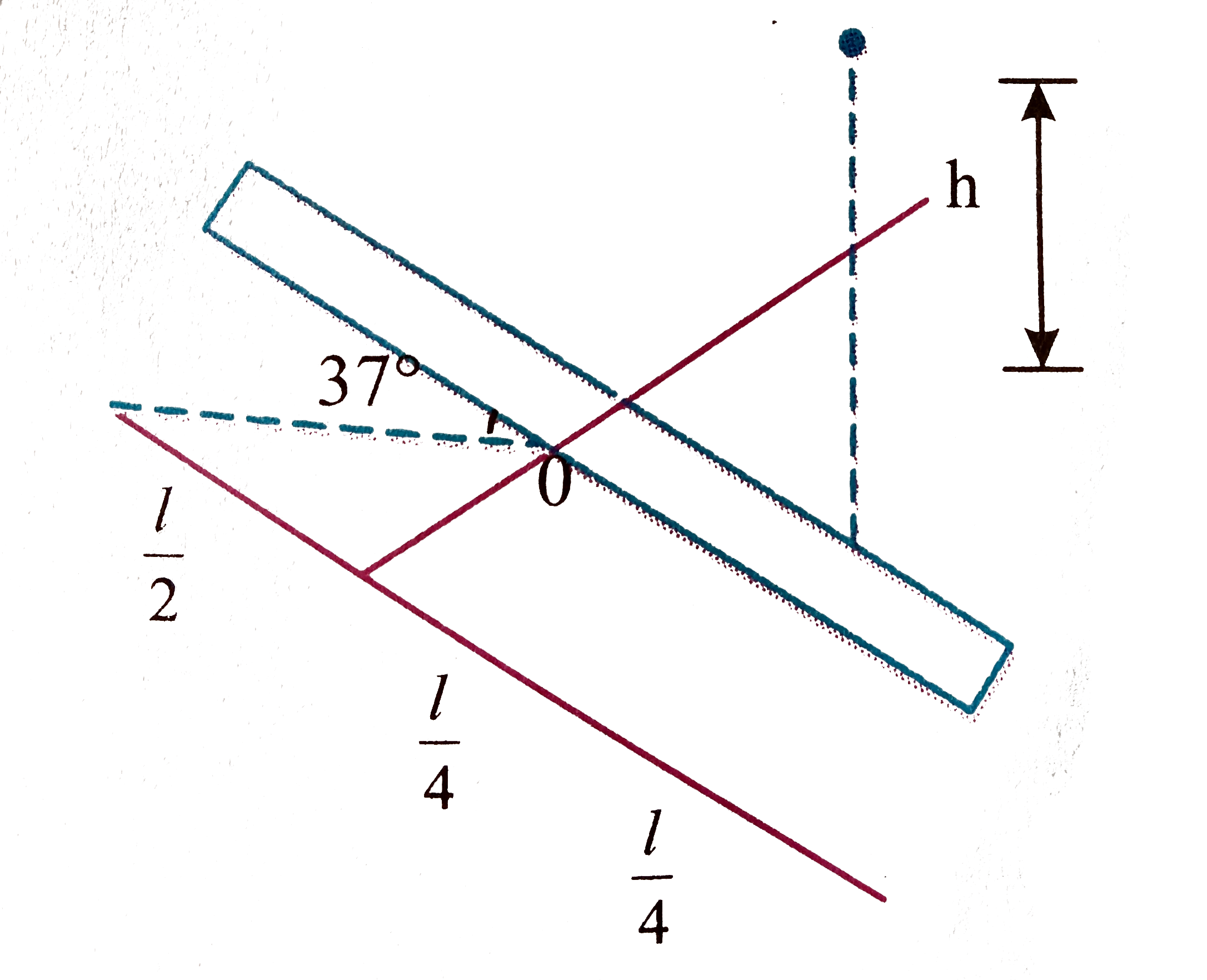
Calculate velocity of the rod just after collision isA1rad/sB3rad/sC2rad/sD4rad/sThe M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
AMl2BMl2/3CMl2/2DMl2/12A thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
A√748LB√548LC√724LD√1924L
A thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its cenre of mass rises to a maximum height of :
View SolutionA rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
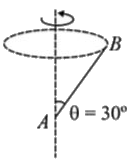
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is

View SolutionMoment of inertia of a rod of mass M and length L about an axis passing through a point midway between centre and end is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution

